補償陽極位置對艦船腐蝕電場防護效果的影響

徐慶林，王向軍，張建春，劉德紅

(1. 海軍工程大學 電氣工程學院，武漢 430033；2. 武漢科技大學 城市學院，武漢 430083)

隨著服役時間的增加，船殼的防腐涂層不可避免地會遭到破損，裸露的鋼質船體與銅合金螺旋槳在海水中形成電偶腐蝕，腐蝕電流流過具有導電性的海水會在船體附近產生腐蝕電場[1]. 學者們研究了海床電導率、海水電導率、溫度、流速、深度等海洋環境因素及潛艇自身潛水狀態對艦船腐蝕電場的影響[2-3]，建立了艦船腐蝕電場等效電偶極子模型，并分析了水平和垂直電偶極子在多層介質中產生的電磁場[4-6]. 由于艦船腐蝕電場對船體周圍的電磁環境產生一定的影響，尤其是給船上電磁通信帶來了很大的干擾，因此，必須對其進行抑制或者消除. 基于艦船消磁思想，通過在船體上安裝電場補償裝置，使補償電流與腐蝕電流在海水中產生的電場方向相反，從而實現降低海水中腐蝕電場的目的[7]. 補償陽極位置是電場補償裝置的重要參數之一，其對腐蝕電場防護效果具有顯著的影響，如何選擇合適的補償陽極位置是電場補償裝置列裝前亟需解決的問題，目前，這方面的研究鮮見報道.

邊界元法廣泛地運用于石油鉆井平臺、海底管道、艦船等各種海洋結構件的腐蝕及陰極保護系統優化問題的仿真[8-10]. 邊界元法是基于加權余量法，將邊值問題轉化為邊界積分方程問題，再利用有限元離散技術構造線性方程組的一種方法[11]，早在20世紀80年代，就有人開始將邊界元法應用于海洋工程結構的腐蝕防腐問題的研究[12-13].

本文采用三維邊界元法建立潛艇腐蝕靜電場模型，并將實驗所測得的非線性極化曲線作為模型的邊界條件，研究補償陽極位置對腐蝕電場防護效果的影響，得到了陽極位置對電場防護效果的影響規律，結合艦船等效電偶極子模型理論合理地解釋了電場防護的原理.

1 邊界元法的基本理論

對于三維腐蝕電場問題，腐蝕介質與電極表面的電位分布符合拉普拉斯方程與下述邊界條件[8,12]為

(1)

(2)

式中：u為海水介質及電極表面的電位；n為邊界外法線；q為電位的法向導數(場強)；u0、q0分別為S1和S2邊界上的u、q恒定值；σ為海水電導率；ia、ic分別表示陽極電流密度和陰極電流密度；fa(ua)、fc(uc)分別表示陽極極化方程和陰極極化方程.

式(1)的等價邊界積分方程為

(3)

式中：ui為Ω域內任一場點i處的電位；ci為常數，當場點i位于光滑邊界面上時，ci=1/2，當場點i位于Ω域內時，ci=1，當場點i位于Ω域外時，ci=0；u(ξ)、q(ξ)分別表示邊界上任一點ξ的電位和電位法向導數；u*(i,ξ)為三維靜態電磁場問題的基本解，其表達式為

(4)

其中r為i、ξ間的距離.

利用有限元離散技術將邊界進行剖分并根據邊界積分方程(3)構造線性方程組，即可求得求解域內的電位，得到海水域中電位分布后，再由極化方程(5)求得電流密度分布，最后由方程(6)求解電場分布.

(5)

(6)

2 模型和實驗

2.1 邊界元模型

利用Solidworks 2016建立潛艇空間直角坐標系下的幾何模型. 考慮到艦船停靠碼頭時，船體左右舷兩側容易被碼頭磨損導致涂層脫落，故設定兩處破損(總破損率為2%)對稱分布于潛艇左右舷兩側. 本文不考慮潛艇的外加電流陰極保護系統(將ICCP視為關閉狀態)，而僅考慮一對電場補償陽極對稱分布于潛艇左右舷兩側. 采用COMSOL Multiphysics仿真軟件中電流分布(邊界元)接口建立潛艇腐蝕靜電場邊界元模型，結合實際情況，將螺旋槳和涂層破損處視為裸露金屬浸泡于海水中，而將船體及舵視為有機涂層完好包覆. 整個模型的求解域及邊界條件設定如下：1)無限空區域為均勻海水介質，電導率σ=4 S/m；2)將碳鋼的非線性極化曲線設置為破損處的邊界條件；3)將銅合金的非線性極化曲線設置為螺旋槳的邊界條件；4)補償陽極為恒電流邊界，其余默認為絕緣邊界. 對潛艇表面進行網格剖分，剖分結果如圖1所示，邊界節點總數為45 973個，邊界三角形單元總數為91 942個，最后采用BiCGStab迭代求解器對模型進行求解.

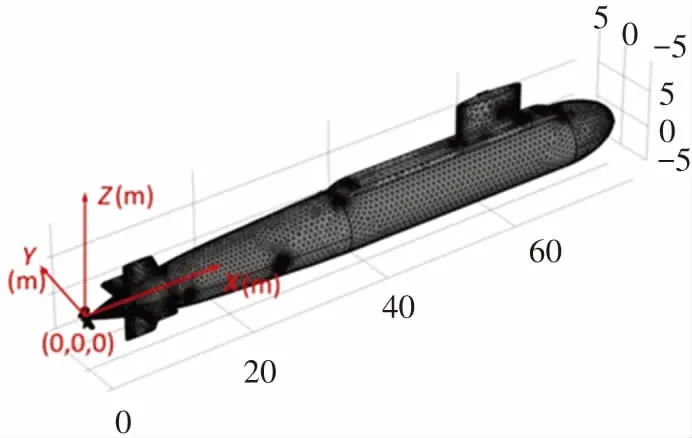
圖1 潛艇三維模型網格剖分示意圖

模擬了補償陽極在6個不同位置的腐蝕電場分布情況，補償陽極中心點坐標分別為：A(1 m, 0°)，B(5 m, 0°)，C1(10. 8 m, 0°)，C2(10.8 m, 45°)，C3(10.8 m, 90°)和D(16.6 m, 0°)，第一個坐標為縱向坐標，即相應點在所建三維坐標系下的X軸坐標，第二個坐標為周向坐標，即相應點到X軸的垂線與XOY平面的夾角. 其中，A、B、C1、D均為0°，研究陽極位置縱向變化對電場防護效果的影響，而C1、C2、C3的X軸坐標相同，研究陽極位置周向變化對電場防護效果的影響.

2.2 動電位極化曲線測試

模型中船殼及舵均采用高強低合金921A鋼，螺旋槳采用耐腐蝕性較好的B10銅合金，采用三電極體系在CS310電化學工作站上測試上述兩種船用材料的動電位極化曲線，實驗介質為電導率σ=4 S/m的NaCl溶液. 其中，工作電極采用環氧樹脂封裝的921A低合金鋼和B10銅合金，試樣尺寸為φ1.1 cm×1 cm，故金屬暴露面積為1.0 cm2，用SiC濕砂紙逐級打磨至1 000目，丙酮脫脂，并依次用乙醇和蒸餾水沖洗，然后置于干燥箱中烘干；參比電極為Ag/AgCl電極；輔助電極為面積S=2 cm2的鉑片電極. 工作電極先在溶液中浸泡一段時間，等到開路電位基本穩定后開始測試，掃描電位為-1.1～0 V，掃描速率為1.0 mV/s.

3 結果與討論

3.1 極化曲線分析

921A鋼和B10銅合金的極化曲線如圖2所示，由圖可知，921A和B10的開路電位分別為-0.68、-0.28 V(參比電極為Ag/AgCl). 由于吸氧腐蝕的氧還原反應速度由氧擴散步驟控制，因此，銅合金的陰極極化電流密度在一定電位范圍內幾乎保持不變，即極限電流密度；而鋼具有較高的析氫過電位，陰極極化過程中氧還原的同時發生析氫反應，故鋼的陰極極化過程中沒有出現極限電流密度. 以鋼為材料的船體破損處和以銅合金為材料的螺旋槳，在海水中形成破損處—海水—螺旋槳—大軸—破損處的回路，從而構成電偶腐蝕，其中，破損處陽極極化發生金屬本身的氧化，如式(7)所示，而螺旋槳陰極極化發生氧還原反應，如式(8)所示.

Fe→Fe2++2e-,

(7)

2H2O+O2+4e-→4OH-.

(8)

圖2 921A鋼和B10銅合金的實測極化曲線

3.2 無電流補償時的腐蝕電場分布

圖3為沒有補償電流時Z=-16 m平面上的電場三分量及電場模值分布，X分量、Z分量和模量均對稱分布于XOZ平面兩側，而Y分量關于XOZ平面反對稱分布. 為了更直觀地分析艦船水下腐蝕電場的分布，選擇以點(-80，16，-16)和點(160，16，-16)為端點的路徑作為觀測對象. 圖4為無電流補償時，電場三分量及電場模量的線分布，EX在X=-16 m和X=68 m附近有正峰值，而在X=25 m附近有負峰值；EY在X=0 m(螺旋槳)附近有負峰值而在X=52.5 m(破損區域中點)附近有正峰值；EZ分布與EY相反；|E|呈現雙峰分布，兩個峰值分別分布在螺旋槳和破損區域中點附近. 以上電場峰值均在10-4V/m數量級.

(a)電場X分量

(b)電場Y分量

(c) 電場Z分量

(d) 電場模量

圖4 無電流補償時指定路徑上的電場線分布

3.3 補償陽極位置對腐蝕電場的影響

本文設定補償陽極的輸出總電流為6 A，通過改變補償陽極位置研究其對艦船腐蝕電場防護效果的影響，圖5為補償陽極在B位置時Z=-16 m平面上的電場三分量及電場模量分布. 由于補償陽極布置在靠近螺旋槳的位置，外加補償電流后艦艉處的電場增大，而涂層破損處的電場減小. 與無電流補償時的電場分布相比，外加補償電流后的電場X分量分布發生較大的變化，艦舯部的負峰值區域明顯減小，而電場Y分量、Z分量和模量沒有明顯變化，均在艦艉和涂層破損處出現電場峰值.

(a) 電場X分量

(b)電場Y分量

(c)電場Z分量

(d)電場模量

圖6為研究路徑上電場三分量及電場模量隨補償陽極位置變化的分布，表1給出了補償陽極在不同位置時電場最大絕對值和相應的電場防護效果. 電場防護效果定義為

(9)

式中：Δ|E|表示電場防護效果，|E|0表示無電流補償時的電場最大絕對值，|E|cur表示外加電流補償時的電場最大絕對值.

當補償陽極在C1、C2和C3位置時，電場線分布曲線幾乎重合，說明陽極位置周向變化對艦船腐蝕電場的影響很小，而陽極位置縱向變化(A/B/C1/D)對電場分布有顯著的影響. 當補償陽極位置改變時，EX分布由對稱曲線變為非對稱曲線，電場正峰值位置保持不變而負峰值移動至螺旋槳附近，EY負峰值位置保持不變而正峰值由破損處向艦艉移動，EZ與EY反對稱分布，隨著陽極位置由艦艉向艦艏移動，電場模量曲線由雙峰逐漸變為單峰，破損處的峰值消失. 由表1可知，隨著陽極位置由艦艉向艦艏移動時，電場補償效果先增大后減小，當補償陽極位于B位置時，腐蝕電場防護效果最好，EX、EY、EZ及電場模量的防護效果分別為48.92%、47.86%、54.55%和49.27%，當補償陽極位于D位置時，電場補償裝置幾乎沒有防護效果.

(10)

(a)電場X分量

(c)電場Z分量

(b)電場Y分量

(d)電場模量

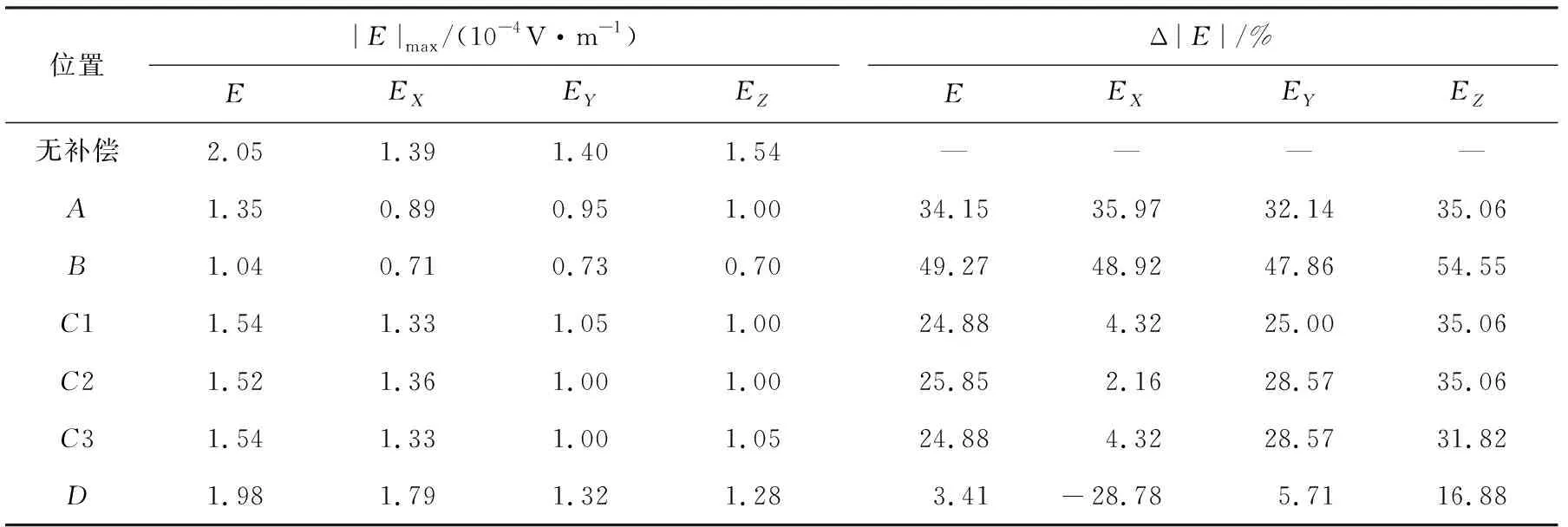
表1 補償陽極在不同位置時電場最大絕對值和相應的電場防護效果

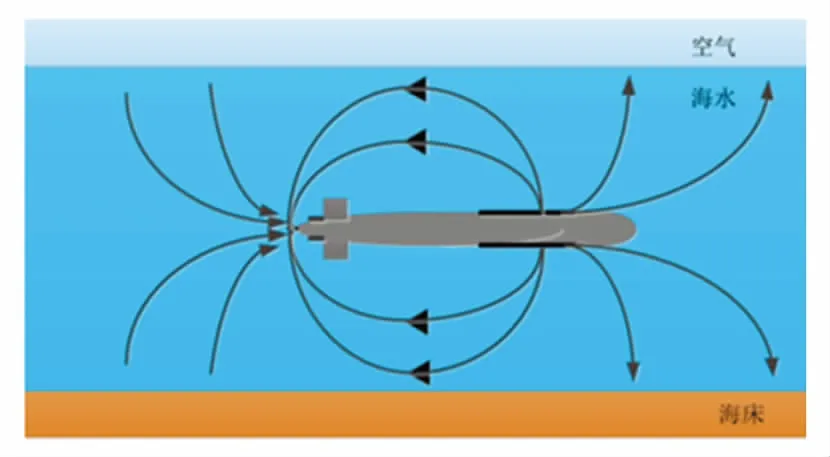
(a)無電流補償時的電流方向

(b)外加電流補償時的電流方向

4 結 論

1)補償陽極周向位置對電場防護效果影響較小，而縱向位置對電場防護效果有明顯的影響.

2)基于靜電場防護原理，補償陽極越靠近螺旋槳，腐蝕電場的防護效果越好，但是當補償陽極與螺旋槳的距離太小時，由于補償電流對螺旋槳起到了陰極保護的作用反而降低了電場防護效果.

3) 當陽極與螺旋槳縱向距離為5 m時，腐蝕靜電場能減少50%左右，當陽極與螺旋槳縱向距離大于16.6 m時，補償電流基本沒有防護效果.