CAN總線中改進的EDF調度算法可調度性分析
王 浩,張鳳登
(上海理工大學 光電信息與計算機工程學院,上海 200082)
0 引言
CAN總線采用面向消息的優先級控制方式,用標識符定義靜態消息優先級,以及其短幀格式和CSMA/CA訪問控制,使得CAN具有極高的可靠性和獨特的設計,特別適合工業過程控制設備的互連[1],因此CAN總線不僅僅局限適用于車體的控制系統中,在艦艇、航天、檢測等控制領域,CAN總線的身影也逐漸增多。從而,國內外的學者均投入了大量精力,針對于CAN總線的調度做研究。最初,由Tindell等人將針對于單處理器的調度分析演化為求消息的最壞響應時間來對CAN總線調度進行分析[2];K.M.Zuberi和K.G.Shin首次提出將EDF算法應用于CAN總線[3],但當時他們提出的方法對CAN做出一些不切實際的假設并且由于時間范圍較短,調度能力的體現有一定的局限性,因而Livani對Zuberi等人的方法進行改進[4];國內對于這方面的研究起步較晚,主要集中于理論研究,例如,諶介人、彭軍等人提出了基于指數分區的EDF算法,一定程度上較平均分區的EDF算法保證了實時性[5];袁暋、檀明等人針對搶占式和非搶占式的EDF調度算法,提出了任務集新的可調度性測試條件[6]。但是,在某些特殊情況下,現有的EDF算法經常會導致CAN總線無法正常通訊調度,因此針對此現象,本文通過優化算法改善總線仲裁機制完成對消息集的調度,提出了一種新的基于雙冪函數分區的EDF調度算法。
1 平均分區EDF算法
1.1 平均分區的EDF算法
EDF(Earliest deadline first)算法是按照絕對截止時間的遠近來分配優先級,即消息的絕對截止時間越近,任務的優先級越高。在這種調度機制下,消息的優先級并不是固定的,而是在每次仲裁前依據截止時間的變化,計算相應的動態優先級,最大程度的保證消息不錯過其截止時間。EDF算法的核心就是將消息的截止時間通過編碼方式轉換為標識符的一部分,通過比較標識符大小判定消息的優先級。但是從實際情況可以看出,隨著時間的增大,消息的絕對截止時間也會無限增大,當增大到一定程度時,由于標識符位數的限制,從而無法對其編碼轉為標識符的一部分。針對于此,文獻[4]中提出相對截止期的概念,因為消息的時間參考點是每一次仲裁開始時間,所以相對截止時間等于絕對截止時間減去仲裁開始時間,定義:
D=d-ts
(1)
式中,D為相對截止時間。隨著ts的增加,D會逐漸減小。根據EDF算法,相對截止時間D會逐漸減小,從而在前一次仲裁失敗的消息其D的減小意味著下次仲裁時優先級的提升。當然,即使通過這種優化,相對截止時間表示的時間范圍仍會很大,因此Livani提出了平均分區的EDF調度算法。對于一組消息{m1,m2,…,mn},其中,相對截止時間為{D1,D2,…,Dmax},并且按照從小到大順序排列。平均分區就是將時間軸等分成k段,最后一段區間需要包含最大的相對截止時間Dmax,一般可以直接將時間軸的最大值設為最大相對截止時間,其中每段的時間長度稱為基本時間單元U。如圖1所示,在每一輪仲裁開始時,根據公式(1)計算出相對截止時間,再根據圖1所劃分的區域判斷相對截止時間在哪個時間段中,再根據當前時間段的區間號來表示消息的優先級。
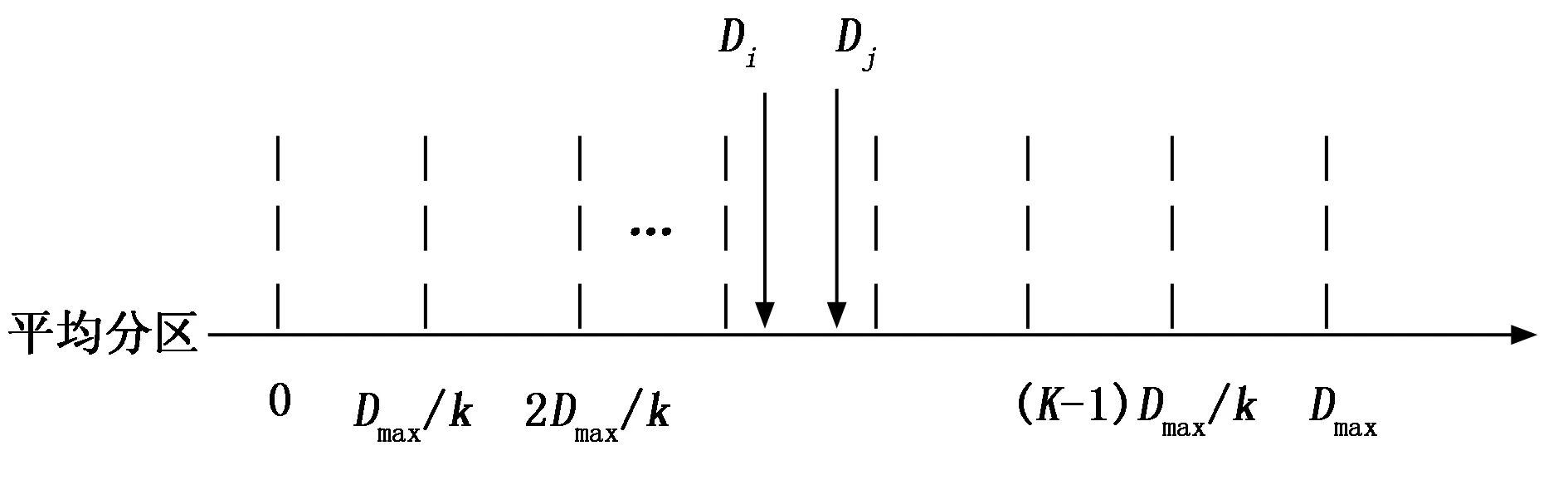
圖1 平均分區示意圖
1.2 量化誤差的分析和影響
由C.L.Liu[7]等人提出的EDF調度算法判定定理:假定存在一個由n個周期性消息構成的任務集{M1,M2,…,Mn},如果消息i滿足如下判定式(2),則該消息可調度。
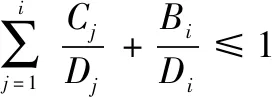
(2)
若任務集中所有消息均滿足上式,則該任務集可調度。
其中:Ci為消息i的傳輸時間,Di為消息i的截止時間,Bi為消息i的最大阻塞時間。
我們通過計算可以得到相對截止時間,盡管這些值可能在數值上的確有些差異,但是在將相對截止時間進行分區時,分割所得到的每個區間是有長度的,無法保障不同的截止時間落到不同的區間中,從而導致不同相對截止時間的消息得到相同的優先級。這是“分區”方案所帶來的誤差,且無法避免,將這種誤差稱之為“量化誤差”。由圖(1)可得,最糟糕的情況下,即兩個相對截止時間分別無限接近于某個區間的上下限,此時量化誤差最大可近似等于基本時間單元U。因此,在量化誤差的影響下,判定式可更新為下式:
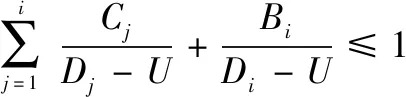
(3)
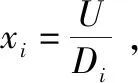

(4)
取max{xi}=x,則:
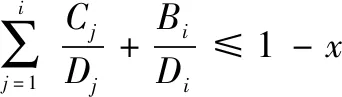
(5)
對比式(2)、(5)可以看出,量化誤差對CAN總線的消息傳輸帶來影響,且使得任務可被調度的條件更為嚴苛。
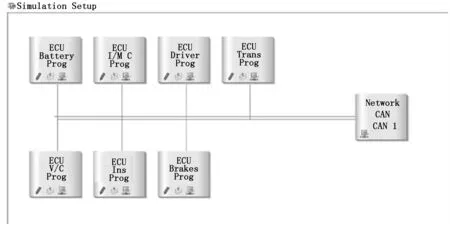
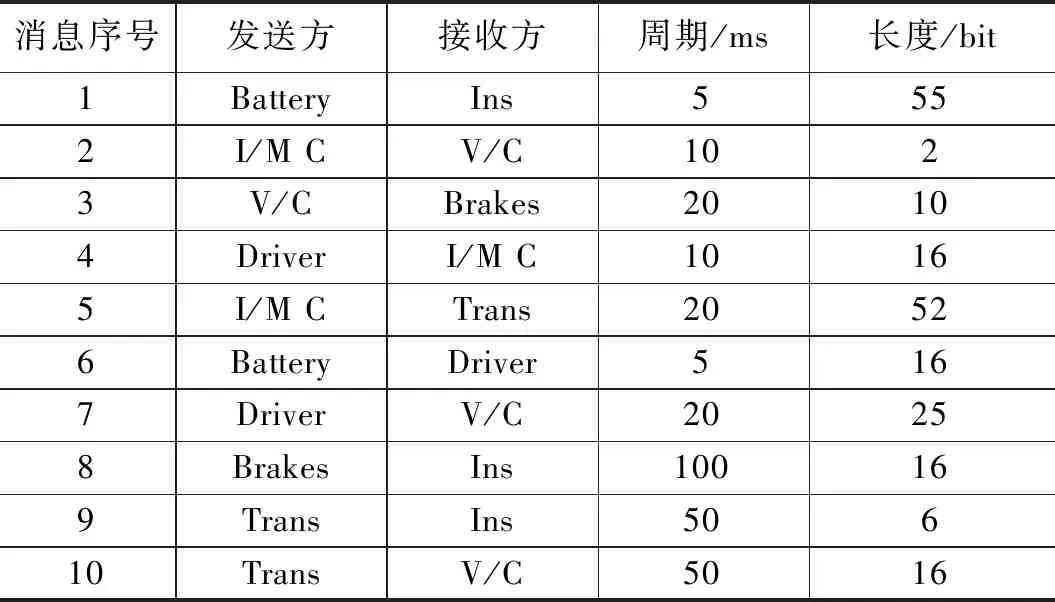
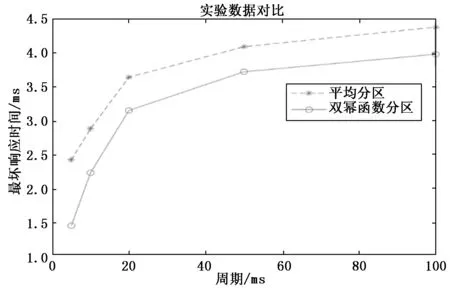
若存在消息mi和mj的標識符分別為Ii和Ij且Ii>Ij,即mj的優先級高于mi。參考圖1,當兩個消息的相對截止時間十分接近時,且Di 由于平均分區的缺陷,使得優先級反轉現象頻出,也正是基于此,本論文提出新的冪函數分區方法。 具體過程如下:采用以a為冪指數的方式對相對截止時間Dmax進行分區,a的值取決于實際的系統情況。為簡化計算,以及考慮到CAN總線通訊時各節點處理器的工作情況,第二次使用冪函數分區時,冪指數取1。冪函數分區使得不同截止期的消息更容易分到不同的母區間內,更好地保證了消息的實時性。分區方法如圖2所示。 圖2 雙冪函數分區示意圖 Ui,j= (6) 令右式記為函數f(x),利用數學方式求極限[8]: 所以如果已有: 則必有: (7) (8) 顯然,滿足判定式(8)時,任務集是可被調度的,各參數的取值取決于實際環境中消息截止期的分布范圍,選取合適的參數值可以獲得合適的分區范圍,從而使得調度性能得到優化。通過對比圖1和圖2可以發現,采用雙冪函數分區時,可以將接近起始時間的區域分區更小,提高精度,從而使得不同截止期的消息可以分配到不同的母區間,有效減少了截止期相近的的消息被分配到同一個母區間內的概率。與平均分區相比,調度的條件也變得更加苛刻,這是保證消息實時性所必須要達到的前提條件。 在上一章節,借助量化誤差的概念理論上給出了消息集可調度的判定準則,接下來我們通過系統模擬方式來驗證是否滿足可調度性。采用系統模擬方式簡單易行,雖然結果不能完全反應系統的真實情況,但能夠作為一種輔助手段去驗證我們提出的雙冪函數分區調度算法。 參考本文所提出的改進的EDF調度算法,采用CANoe平臺進行仿真實驗。CANoe的主要組成部分:模擬界面編輯、CANdb++編輯器、CAPL瀏覽器、面板設計等。目前市面上流行的幾種總線,如CAN、LIN、FlexRay、以太網等,均可在CANoe上實現仿真測試。通過CANoe可以將所有節點虛擬化,對于各個節點相應的通信數據可以使用CANdb++編輯器建立所需要的數據庫,并通過CAPL語言編寫各CAN節點程序實現節點間的通訊、錯誤處理等。 此外,汽車工程師協會(SAE)提供了一個“基準”應用[9],其描述了在原型電動汽車上的7個不同子系統之間發送的一組信號。盡管這個汽車控制系統是使用點對點鏈路設計的,但是這組信號為說明CAN總線在復雜分布式實時控制系統中的應用提供了一個很好的例子,因此,針對于本次實驗,我們將通過CANoe搭建出此網絡通信模型。其中7個子系統分別是:電池(Battery),車輛控制器(V/C),逆變器/電機控制器(I/M C),儀表盤顯示(Ins),驅動器輸入(Driver),制動器(Brakes),變速器控制(Trans),如圖3所示。 圖3 節點示意圖 連接這些子系統的網絡需要處理總共53個信號,按照信號的接收方、發送方、信號周期以及信號長度等要求將信號打包成10個消息,如表1所示。根據表中信息,通過操作CANdb++,將所有信號打包封裝,并且對該網絡的相關參數進行配置,如波特率、采樣點等。根據表1消息矩陣中消息的周期分布情況,同時在滿足判定式(8)的前提下,可將分區中各參數選取為:a=2,k=16,q=8。 表1 消息矩陣 CAN網絡中的節點在收發消息時,依據本文所提出的雙冪函數分區EDF調度算法,利用CAPL編程對消息以及通訊進程進行動態處理,以實現合理的調度。具體實現過程如下:在本文的調度機制下,CAN節點在發送消息前,計算該消息的相對截止時間,然后依據所得相對截止時間算出對應的母區間和子區間號,將對應的區間號轉換為消息的優先級并進行進制轉換得到消息的標識符,再根據當前的標識符進行仲裁。部分程序設計如下所示: if(msg4.DIR!=TX) { t_new=timeNow()/100000.0+0.16; write("t_new=%f",t_new); D=d-t_new-init; count++; if(D>0.001&&D<62.5) { g=1; h=_floor(7-(1000.0/(16*D))); } else if(D>62.5) { g=_floor(5-exp(1000/D)); h=_floor((exp(6-g)*6*D-7000)/(exp(6-g)*D-1000)); } p=h+(g-1)*5; write("p4=%d",p); p=0x14-p; p=p<<18; 對于雙冪函數分區調度算法的網絡性能分析,我們主要將關注點放在最壞響應時間上,最壞響應時間是消息的最大時延,即消息在隊列中的最長排隊時間和傳輸時間的總和,因此實時性的強弱在數據上最直觀的體現就是最壞響應時間的大小。其中,挑選出5組周期差別較大的消息通過對比平均分區方法來驗證雙冪函數分區的優越性。每組實驗3次后計算“消息最壞響應時間”的平均值,實驗結果如圖4所示。 圖4 消息最壞響應時間 結合實驗結果,對比傳統的基于平均分區EDF調度算法,我們可以發現本文提出的基于雙冪函數分區方法所具有的優點: 1)針對于消息集的截止期,采用傳統的平均分區EDF調度算法(分區大小為2 ms),在對標識符進行編碼時至少需要7位才能夠滿足編碼要求,而采用本文的方法,只需要6位就可以滿足需求。 2)通過計算可以得知,在本文的試驗參數下,最小的子區間大小約為0.05 ms,相較于平均分區的2 ms,明顯提高了分區精度,換言之,在經歷一段時間后,消息的截止期在不斷地減小,那么仍然會導致多個消息的截止期落在同一個分區內,從而獲得同樣的優先級,而本文的雙冪函數分區方法可以將截止期劃分至微秒級,從而保證了較高的辨識度。 3)采用雙冪函數分區的EDF調度算法,可以降低消息集的最壞響應時間,從圖5中可以觀察到20 ms以內的消息,即高優先級消息,最壞響應時間的減少尤為明顯,這也驗證了第二點,雙冪函數分區現在對較小的截止期上依然保證了很強的辨識度。 顯然,通過雙冪函數分區的方法進行調度,分區誤差進一步減小,對于截止期最終落在哪個分區更為精確,降低了因優先級反轉而無法調度的情況,使得消息的最壞響應時間得到了有效的縮減,從而提高了網絡傳輸的實時性。 本文對比平均分區EDF調度算法,對于量化誤差引起的消息不可被調度問題,引入一種雙冪函數分區的方法。理論分析量化誤差對該方法的影響,并論證了該方法使用時消息可調度的判定條件。實驗證明了本文的雙冪函數分區調度算法對消息的截止周期進行合理的分配,從而克服了傳統EDF算法在調度方面的不足,優化了消息的最壞響應時間,提高系統實時性,對于EDF調度算法在實際中更好的應用于CAN總線通信優化中起著指導作用。2 雙冪函數分區EDF算法
2.1 雙冪函數分區的EDF算法
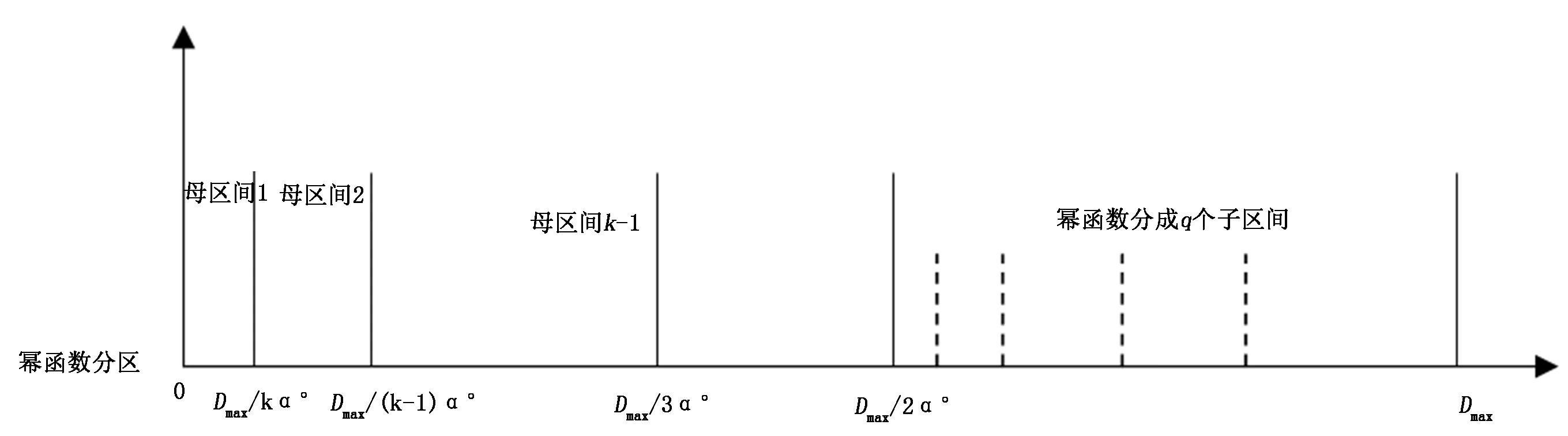
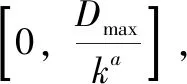
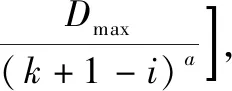
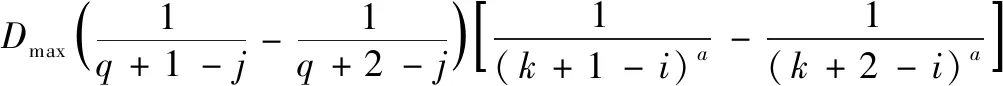
2.2 可調度性分析
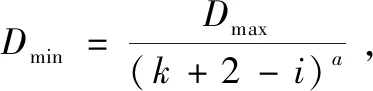
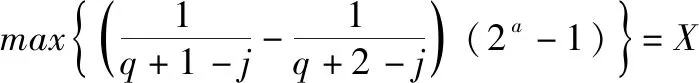
3 實驗驗證與分析
4 結束語

