二自由度電液振動臺沖擊波形再現控制算法研究

吳智睿， 關廣豐， 熊 偉， 王海濤

(大連海事大學 船舶與海洋工程學院， 遼寧 大連 116000)

引言

沖擊是一種確定性、非周期性的瞬態振動，例如飛機的著陸、導彈的發射、電子設備的偶然掉落、汽車的碰撞等[1]，其危害尤為突出。對試件進行沖擊測試是可靠性試驗的重要組成部分。

電液振動臺是大型結構件進行沖擊振動環境模擬的關鍵設備。控制系統是多軸電液振動臺的核心技術。電液振動臺控制系統由伺服控制和振動控制組成，伺服控制系統用于實現振動臺加速度控制,提高系統阻尼，改善系統的穩定性，提高系統頻寬。 常用的伺服控制技術包括三狀態控制、自適應控制和自抗擾控制等[2]。但伺服控制無法使系統幅頻特性穩定在0線上,因而對于沖擊振動這種短時瞬態的振動，無法精確地再現沖擊波。

振動控制系統通過迭代方法修正伺服系統的驅動信號，減小響應信號與參考信號之間的偏差。20世紀70年代到90年代初，美國Sandia國家實驗室SMALLWOOD的團隊[3-4]全面闡述了振動控制的理論和算法，提出了沖擊響應譜(SRS)的迭代計算方法，并且還給出了驅動信號的反饋修正算法。隨后美國Synergistic Technology Incorporated(STI)公司用數字系統完善了多激勵器的正弦、隨機、沖擊等振動試驗控制系統[5]；UNDERWOOD等[6]提出采用自適應控制算法進行正弦振動模擬實驗。STEWART等[7-8]利用單軸電液振動臺進行了爆炸沖擊模擬試驗。但這一時期的振動臺控制系統主要采用離線迭代的控制方法，離線迭代采用的是牛頓算法，牛頓算法需要實時計算阻抗的逆，但系統阻抗是實時變化的，所以無法跟蹤系統頻率特性的變化，導致系統控制精度不夠。

為提高多自由度沖擊波再現控制精度，本研究在傳統的多軸波形再現算法基礎上提出基于BFGS算法的優化算法的多自由度沖擊波形再現控制方法。BFGS算法是擬牛頓法的一種，是BROYDEN、FLETCHER、GOLDFARB、SHANNO 4位學者所研究，并以名字首字母命名的，是用正定矩陣替代牛頓法中的海森矩陣的方法。本研究首先簡介二自由度電液振動臺系統，然后給出了BFGS算法的基本原理，并推導基于BFGS算法的驅動譜迭代公式，設計波形再現控制算法。最后，通過仿真結果驗證基于BFGS算法的波形再現控制算法的有效性。

1 二自由度電液振動臺簡介

本研究的二自由度電液振動臺結構示意圖如圖1所示。4個液壓激振器作為驅動件通過上下虎克鉸支座分別與振動臺的上下平臺連接，上平臺通過大虎克鉸與支座相連，上平臺可繞大虎克鉸中心做二自由度轉動，分別是繞x軸的rx自由度和繞y軸的ry自由度。

圖1 二自由度電液振動臺結構示意圖

振動臺具體結構尺寸及元件參數，可參考文獻[9]。文獻[10]詳細介紹了圖1所示兩軸電液振動臺的伺服控制系統及其實現方式。

2 波形再現控制系統設計

波形再現控制系統的原理是根據系統的頻率特性，對輸入信號進行循環補償校正，最終使系統輸出的響應信號與參考信號在一定誤差允許范圍內。

設系統輸入的時域信號為D(t)，輸出的時域信號為C(t)，頻響函數為H(f)；D(t)經傅里葉變換轉化為頻域驅動譜D(f)；C(t)經傅里葉變換轉化為頻域響應頻譜C(f)，C(f)=H(f)D(f)；參考信號為R(t)；R(t)經傅里葉變換轉化為頻域參考譜R(f)；誤差譜為E(f)，E(f)=R(f)-C(f)；阻抗為Z(f)，Z(f)=H-1(f)。

傳統波形再現控制算法中驅動譜D(f)的迭代公式為：

Dn+1(f)=Dn(f)+βZ(f)(R(f)-Cn(f))

(1)

式中，β—— 修正系數，無量綱

Dn(f) —— 迭代第n次的驅動譜

n—— 迭代次數

式中，Z(f)由H(f)初值確定， 在迭代過程中并不更新。實際系統中，頻響函數是一直在變化的，所以利用上述驅動譜更新公式來控制系統，會出現較大誤差，多次迭代后更會出現直接發散的情況。

基于擬牛頓方法實時更新系統阻抗，有利于提高波形再現的控制精度。波形再現的目標是使得系統響應譜與參考譜之間的誤差譜盡可能小。可以以此設定目標函數，其中驅動譜D(f)為自變量。

F[D(f)]=||R(f)-H(f)D(f)||2

(2)

根據牛頓法推導出系統驅動迭代公式為[11]：

Dn+1(f)=Dn(f)+βTn(f)(R(f)-Cn(f))

(3)

式中，Tn(f)為廣義阻抗。對比式(1)和式(3)可知，Tn(f)代替了傳統阻抗Z(f)。利用BFGS擬牛頓算法對Tn(f)進行迭代更新。BFGS算法迭代公式為[12]:

(4)

式中，Bn，Bn+1分別表示第n次和第n+1次迭代矩陣；Sn為迭代步長；Yn為梯度差。文獻[13]證明了BFGS算法具有全局收斂性。二自由度電液振動臺系統是非線性系統，對于非線性系統，BFGS算法局部超線性收斂。

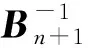
(5)

(6)

式中，I為單位矩陣。由于本系統中涉及迭代的矩陣中含有復數，所以只需將算法里的迭代公式中的轉置換成共軛轉置。

將Tn(f)帶入式(6)中可得到Tn(f)的迭代公式為:

(7)

式中,Sn=Dn+1(f)-Dn(f)

3 仿真模型搭建

圖2所示為沖擊波形再現優化算法模型。其中“Tn(f)迭代”模塊用于實現式(7)；“驅動譜迭代”模塊用于實現式(3)；FFT表示傅里葉變換；IFFT表示逆傅里葉變換。“伺服控制系統”模塊參考文獻[10]。

圖2 沖擊波形再現控制優化算法模型

4 仿真分析

4.1 仿真參數

通過rx和ry二自由度的沖擊波再現仿真，檢驗BFGS算法的有效性。rx和ry二自由度參考沖擊波形加速度如式(8)所示：

(8)

分別采用傳統的波形再現控制方法和基于BFGS的優化算法進行沖擊波再現。參考沖擊波峰值加速度為1 rad/s2，脈沖寬度為50 ms，緩沖波形最大加速度為0.2 rad/s2，緩沖帶寬度為兩側各100 ms。

4.2 沖擊波再現控制算法指標分析

BFGS算法是自適應算法的一種，其優點是不用手動調節許多參數，跟迭代算法一樣，其精度受算法本身的收斂性和收斂速度影響。沖擊試驗時系統頻率特性發生變化，頻率特性變化速度大小會影響系統跟蹤誤差，系統頻率特性變化要比算法收斂速度慢，算法的收斂速度越快，收斂精度越高，系統的跟蹤誤差就越小。

常用的波形再現誤差計算公式為[10]：

(9)

由式(9)可知，e值越小，波形再現的效果越好。

除式(9)所示峰值誤差外，對于沖擊波形，文獻[14]給出一種專用于沖擊波再現控制的指標。對于單軸試驗系統，沖擊波形在其主要沖擊波時間段內，確保系統的真實響應波形控制在參考波形的±20%容差限內；對于多軸試驗系統，可參考單軸試驗系統。

本研究同時采用上述兩個指標，衡量沖擊波再現控制精度。

4.3 仿真結果

分別給出僅采用伺服控制算法、傳統波形再現算法和基于BFGS算法的波形再現控制算法三種情況下的沖擊波再現曲線。

對負載進行沖擊試驗時，一般要求負載在規定的沖擊曲線容差限內進行有限的沖擊次數。每次沖擊試驗的曲線效果類似，研究僅需給出典型的1個周期沖擊波形即可。為了顯示清晰，只選取波形在3.8～4.3 s內的波形再現仿真結果。

圖3所示為僅采用伺服控制仿真曲線，響應波形在大部分時段超出了參考波形±20%容差限。rx自由度最大誤差為81%，ry自由度最大誤差為30%。可知，僅采用伺服控制，無法實現參考沖擊波的高精度再現。

圖3 僅采用伺服控制時沖擊波再現曲線

為了驗證BFGS波形再現算法的有效性，利用增益突變，模擬實際系統在沖擊測試中出現的頻率特性改變。在第4次迭代后調節系統增益，rx自由度增益由1.2變為1.5；ry自由度增益由0.4變為0.5。圖4和圖5所示為第3次迭代后，傳統算法和BFGS優化算法仿真曲線，傳統算法大部分時間段在容差限內，而BFGS算法全部時間段在容差限內；圖6和圖7為第25次迭代后，傳統算法和BFGS優化算法仿真曲線，傳統算法響應超出了容差限，BFGS算法響應在容差限內; 表1給出了圖4～圖7仿真曲線中沖擊波再現的最大誤差值。由表1可知，傳統算法在系統發生突變前后的誤差較BFGS算法的誤差都大，25次迭代后，傳統算法出現很大誤差，BFGS優化算法誤差較小，滿足±20%容差限沖擊試驗標準。

圖4 傳統算法第3次迭代后波形再現曲線

圖5 BFGS算法第3次迭代后波形再現曲線

圖6 傳統算法第25次迭代后波形再現曲線

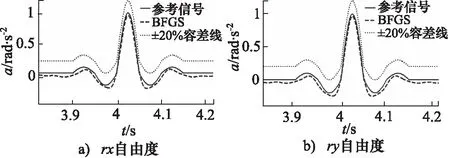
圖7 BFGS算法第25次迭代后波形再現曲線

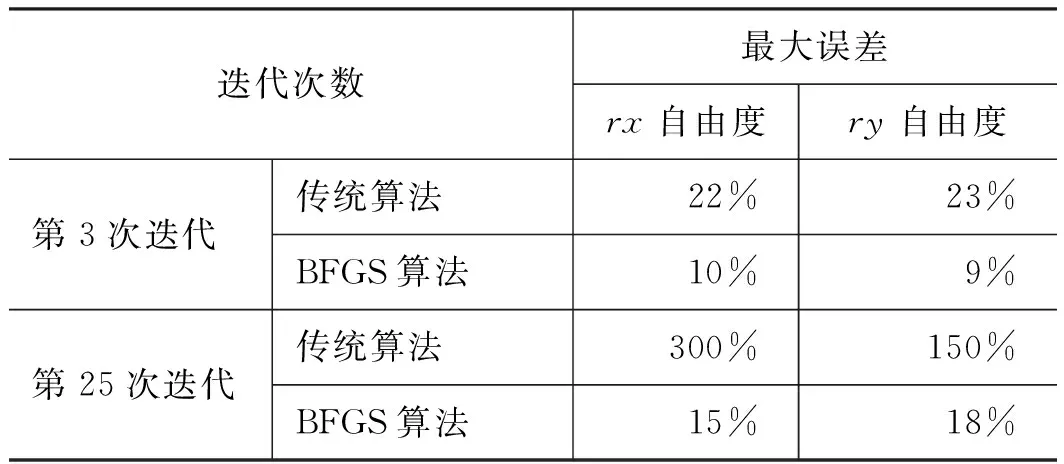
表1 rx, ry自由度沖擊波形時域最大誤差

圖8所示為系統時域波形振幅最大誤差。第4次迭代后系統增益發生突變，傳統算法中rx自由度和ry自由度誤差都在15次迭代后大于150%，且還有不斷上升的趨勢，系統趨于發散；而BFGS算法在突變之后，rx自由度和ry自由度誤差雖有所增加，但都控制在參考波形的±20%容差限之內，驅動信號收斂，算法具有良好的穩定性。

圖8 時域波形振幅最大誤差

5 結論

針對傳統控制方法受負載特性變化等因素的影響不能保證參考沖擊波形的再現精度，提出了基于BFGS算法的波形再現控制策略，實時更新時變系統的廣義阻抗。

基于MATLAB/Simulink平臺建立二自由度電液振動臺的模型，設計BFGS算法的波形再現控制器，利用增益突變，模擬實際系統頻率特性的變化，測試BFGS算法有效性。仿真結果表明,BFGS算法可有效的提升系統沖擊波形再現的控制精度。

本研究提出的算法不僅適用于二自由度沖擊波再現系統，亦可推廣應用于多自由度隨機波形再現控制系統。