基于改進一次二階矩方法的數字液壓閥可靠性研究

郝露菡， 付康平， 俞 濱， 婁文韜， 馬國梁， 秦海興

(1.燕山大學 機械工程學院， 河北 秦皇島 066004；2.燕山大學 國家冷軋板帶裝備及工藝工程技術研究中心, 河北 秦皇島 066004；3.北京華德液壓工業集團有限責任公司， 北京 100176)

引言

隨著計算機技術的飛速發展，液壓元件與計算機融合是一個熱點關注話題 ，實現計算機對液壓系統的精確控制是液壓技術發展的必然趨勢[1]。數字閥不易受外界環境干擾的影響，具有結構簡單、抗污染能力強和維護方便等優點，現已成為熱點研究方向。數字閥作為液壓控制系統的關鍵元件，一旦出現故障，排查困難，嚴重影響到經濟效益，因此對液壓閥的可靠性研究具有重要意義[2-6]。目前可靠度的理論方法中一次二階矩法、蒙特卡洛模擬法、隨機有限元法等方法已經發展多年，并且應用到建筑結構、電路系統、機械結構設計等各個研究領域，為該領域可靠性研究發展起到重要的指導作用[7-11]。由于液壓系統的應用領域十分廣泛，所以關于液壓系統的可靠性研究方法具有十分重要的意義，通過本研究給出了液壓系統可靠性研究的方法，對后續液壓系統的可靠性研究具有重要的借鑒意義。

以某增量式數字液壓閥為研究對象，建立數字閥的可靠性極限狀態方程，采用基于改進的一次二階矩方法，通過MATLAB編程找到合理的驗算點，研究數字閥在極限工況下(閥芯開度5 mm)，不同供油壓力對其可靠性的影響，估算數字閥的可靠度。

1 改進的一次二階矩

1.1 可靠性分析基本概念

可靠性的定義為在規定的時間內和規定的條件下，結構完成規定功能的能力。可靠度為在規定的時間和規定的條件下，結構機構完成規定功能的概率。因此可靠性分析就是系統行為或者說系統響應量滿足規定要求的概率分析。

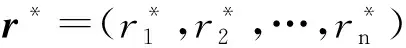
系統失效的概率稱為失效概率Pf，系統安全的概率稱為可靠度Pr。相應的數學表達式為:

Pf=P{F}=P{Z(x)=r(x)-r*≤0}

(1)

Pr=P{S}=P{Z(x)=r(x)-r*≤0}

(2)

1.2 一次二階矩

一次二階矩方法(FOSM)是可靠性分析中的經典方法，基本思想是將非線性的功能函數進行線性化展開，通過基本變量的一階矩和二階矩來計算線性化后的功能函數的一階矩和二階矩，進而近似得到功能函數的失效概率。一次二階矩法包括均值一次二階矩(MVFOSM)和改進的一次二階矩法(AFOSM)，二者的主要區別是線性展開點不同，MVFOSM在基本變量的均值點處進行線性化，而AFOSM則是在失效概率貢獻最大的點進行線性化，即最可能失效點(驗算點)處進行線性化。兩種方法的基本原理相同，但是均值一次二階矩法計算得出的可靠性指標受功能函數形式的影響較大，不同的功能函數得到的結果不同。所以提出一種改進的一次二階矩法，此方法擺脫功能函數形式的約束，適用性更強，是目前流行的可靠性分析方法。

1) 一次二階矩(中心點法)

設X=(X1,X2,…,Xn)T為結構基本隨機變量，非線性功能函數的一般形式為:

Z=gX(X)=gX(X1,X2,…,Xn)

(3)

當在某一點x0=(x01,x02,…,x0n)T將Z展開成級數并取至一次項，即:

Z≈ZL=gX(x0)+(X-x0)T▽gX(x0)

(4)

μZL=gX(μX)

(5)

(6)

按中心點法計算的可靠度為:

(7)

式中，β為可靠性系數。

中心點法算式簡單，但是結果對功能函數的依賴性較強，不同的功能函數產生的結果往往不同，甚至出現很大的差異。不同功能函數算出來的β不唯一。

由此可以得到一次二階矩方法的可靠度PR和失效概率Pf為:

(8)

(9)

一次二階矩的方法選取不同的功能函數會產生不同的可靠性系數，有時會導致失效率產生很大的差距，即可靠性系數對功能函數的依賴性很強。

2) 改進的一次二階矩(驗算點法)

(10)

若設計點在失效面上，則gX(x*)=0，但是在最開始迭代的時候不一定能夠找到準確的失效面上的點，所以在公式中依然保留這一項。

(11)

式中，λi為靈敏度系數。

進行變形計算：

(12)

于是有:

(13)

式中，θYi為自變量與均值向量的夾角。

可靠指標β就是標準化正態空間中坐標原點到極限轉態面的最短距離，與此相對應的極限狀態面上的點p*就稱為設計驗算點，常稱為驗算點或設計點。

驗算點法β的迭代求解步驟:

(1) 假設初始驗算點x*，一般取x*=μX；

(2) 計算λi；

(3) 計算β；

(4) 計算新的x*；

(5) 以新的x*重復步驟(2)至步驟(4)，直至前后兩次║x*║之差小于允許誤差ε。

流程說明：

(1) 先取一個驗算點，一遍先選取均值點；

(2) 將均值點帶到靈敏度λi計算公式中，求出靈敏度的值；

2 數字閥可靠性建模

2.1 數字液壓閥原理分析

某型號增量式數字閥結構如圖1所示。

其工作原理如下：步進電機1與螺套10通過鍵固連，步進電機1帶動螺套10旋轉相同的角度，螺栓2與閥芯7通過圓柱銷8固連，螺栓螺套結構將螺套10的轉動角度轉換為閥芯7的位移，通過控制閥芯的不同位置，最終實現液體的方向和流量控制，限位結構4、端蓋5和限位螺栓6起軸向限位和轉動限位的作用。

1.步進電機 2.螺栓 3閥體 4.限位結構 5.端蓋6.限位螺栓 7.閥芯 8.圓柱銷 9.電機支架 10.螺套圖1 某增量式數字閥結構原理圖

2.2 可靠性建模

綜合數字閥結構、推力-扭矩轉換關系等因素，在數字閥薄弱環節絲杠上構建該數字閥的極限狀態函數，以絲杠出現破壞、磨損情況為該數字閥失效情況。在多種受力條件下絲杠螺紋受力情況作為響應量，所以其功能函數等于螺紋實際抗力應力Ra減去螺紋實際所受載荷應力Sa。

1) 抗力應力分析

由于結構抗力受到材料不確定性、幾何不確定性、計算模式不確定性等影響，使得結構具有不確定性，該結構采用螺栓、螺套均為標準件，采用的計算公式是常規公式準確性高。所以在該數字閥螺栓、螺套結構中只考慮材料不確定性，即僅考慮材料性能系數Km。

該數字閥螺栓、螺套選型尺寸為M8，導程ph，大徑D，小徑d，材料為Q235普通碳素鋼。根據統計數據得出Q235普通碳素鋼材料性能系數服從正態分布，其均值，變異系數，屈服極限為235 MPa，安全系數為1.5，所以許用應力 [Rσ]=156.7 MPa，由于螺栓螺套就是該結構的整體構件，所以該結構的實際抗力和許用抗力關系為:

Ra=Km·[Rσ]

(14)

2) 荷載應力分析

該數字閥是由螺栓與液壓閥閥芯連接，螺栓受到的力為閥芯的液動力(不考慮摩擦力)。當閥芯開度達到最大值時受到的液動力最大，在該極限狀態下建立極限狀態方程。當開度達到最大時運動瞬間忽略慣性力和摩擦力，所以只考慮閥芯所受到的穩態液動力。

由于荷載應力分析是取整個荷載過程的最大應力進行分析，所以也考慮在數字閥的極限狀態，即閥芯開度達到極限值時(該數字閥極限開度為5 mm)受力情況作為響應量，建立系統供油壓力最大、閥芯開度最大時螺栓螺套受力情況的螺紋極限狀態方程。并研究數字閥在極限工況下(閥芯開度5 mm)，不同供油壓力對其可靠性的影響。

閥芯受到穩態液動力為:

Fs=0.43W(ps-pL)xv

(15)

式中，W—— 閥芯開度，mm

ps—— 供油壓力，MPa

xv—— 閥芯位移，mm

pL—— 負載壓力，MPa

考慮空載情況下荷載受力最大，此時穩態液動力為：

Fs=0.43Wpsxv=Kfoxv

(16)

其中，Kfo為空載液動力剛度。

螺紋受力面積近似為:

(17)

式中，D—— 螺栓大徑，mm

d—— 螺栓小徑，mm

A—— 螺紋受力面積，mm2

則荷載為：

(18)

由于閥芯加工尺寸的不確定性，導致受到荷載具有不確定性。則：

xv=KAxsv

(19)

式中,xv—— 閥芯實際位移，mm

xsv—— 要求達到的位移，mm

KA—— 幾何不定系數，經過經驗統計得出μKA，VKA

3) 數字液壓閥功能函數

通過前面的抗力分析和荷載分析得出功能函數為:

(20)

當Z>0時，數字閥為可靠狀態Z<0時，閥芯為失效狀態[16-19]。

3 數字閥可靠性系數計算

增量式數字液壓閥的具體參數如表1所示。

表1 數字閥結構參數

將表1中結構參數帶入功能函數得到具體表達式為:

=156.7×Km×106-149.19×KA×106

(21)

狀態方程的梯度為：

=(156.7×106-149.19×106)

(22)

利用MATLAB編程計算得出:

Pf=0.0076

在供油壓力ps=7 MPa時，增量式數字閥的失效概率為0.0076，可靠度為0.9924。

同樣的計算方法，可以估算出在不同壓力條件下該數字法的可靠度。在供油壓力ps=14 MPa時，數字閥可靠度大約為0.9168。在供油壓力ps=21 MPa時，數字閥可靠度大約為0.8631。

綜上所述，該增量數字閥的可靠性隨供油壓力的增加而遞減，該數字閥在正常工況下(ps=7 MPa)時，數字閥的可靠性較高[20-22]。

4 結論

通過改進的一次二階矩方法對某增量式數字閥進行可靠性分析，建立極限狀態方程，利用MATLAB編程計算出失效概率，得出如下結論：

(1) 利用改進的一次二階矩法計算出增量式數字閥在供油壓力為7 MPa時的可靠度為0.9924，隨著供油壓力的增大，可靠度會隨之下降。供油壓力的大小是該數字閥可靠度的關鍵因素；

(2) 通過MATLAB編程，實現了工程實際建模與數理算法的有機結合，簡化了可靠性試驗的程序。算法具有通用性，利用MATLAB編程能夠實現各種模型的可靠度計算，節約成本、提高效率。

相比較可靠性試驗來得到數字閥可靠度的方法，利用改進的一次二階矩方法進行可靠性分析可以節約大量成本。改進的一次二階矩法不依賴極限狀態方程模型具體形式，具有更好的適用性。通過該方法計算出的可靠度可以作為可靠性試驗數據提供理論參考。