問題驅動下指向高階思維的課堂實踐

翁玲玉 陳建國

[摘? 要] 文章以“函數圖像會說話”專題課為例進行教學探索，以問題為驅動，組織學生進行指向高階思維的學習活動，讓學生經歷疑題引入、開放拓展、導學探究、變式評價的活動過程，來激活思維、開拓思維、延伸思維、創造思維.

[關鍵詞] 高階思維;問題驅動;函數圖像;專題教學

根據美國著名教育家布盧姆對認知過程的劃分，數學界將數學高階思維的初步定義如下：數學高階思維，是指在數學活動中發生的較高認知水平層次上的心智活動或認知能力. 杜威認為反省思維是一種高階思維，并且提出了“思維五步”[1]. 鐘志賢教授指出，分析、綜合、評價和創造是高階思維在教學目標中的分類表現，認為高階思維主要由創新能力、問題求解能力、批判性思維能力和決策力構成[2]. 由此可見，數學高階思維能力分別由問題解決能力、探究能力、推理能力、構思能力和創造能力等構成.

問題驅動課堂是以學生為中心、以思維為核心、以問題為主線的“兩心一線”三個關鍵要素，將“內容問題化，問題思維化，思維實踐化”，培養學生的高階思維能力. 筆者在“函數圖像會說話”一節的教學中，以問題為載體，不斷豐富問題背景，在問題驅動下進行探究，組織學生進行指向高階思維的學習活動，讓學生經歷“問題思考——問題分析——導學交流——判斷質疑——評價創造”的高階思維過程，主要從以下方面來進行實踐：疑題引入，激活思維;開放拓展，開拓思維;導學探究，延伸思維;變式評價，創造思維. 促使學生通過問題驅動下的課堂實踐，使學生的高階思維能力得以提升.

問題驅動下指向高階思維的課

堂實踐

1. 疑題引入，激活思維

問題1? 某飛機著陸后進行滑行，滑行路程s（米）與滑行時間t（秒）的函數關系為s=60t-1.5t2，問：著陸后滑行多長時間該飛機才能停下來

教學片段：

（學生通過畫圖，思考片刻……）

生A：畫出圖像，如圖1可知，滑行40秒后才能停下來.？搖？搖？搖

師：善于通過函數圖像來解決問題，這非常好！40秒滑行的路程s是多少米？

生A：t=40時，s=0，感覺不太對勁，呵呵.

生B：應該是20秒后才能停下來.

師：為什么？

生B：根據實際，A同學的圖像錯了，應該取函數圖像對稱軸的左邊部分.

師：真棒！由此可見，函數圖像確實會說話，可以告訴我們很多信息，但圖像首先要符合實際，同學們要重視這類“易錯題”，要加大對這類“疑題”進行研究與反思.

設計意圖? 數學思維的起點和動力是問題，通過易錯問題引入，可以激活學生的思維. 由于學生平時的錯題資源很多，我們要加以選擇. 錯題釋疑，讓學生更容易被吸引并積極參與課堂交流. 本節課是“函數圖像會說話”的教學復習專題，繞不開發展數形結合思想，圖像的正確與否將直接影響學生的思維，教學中利用疑題引入除了激活思維，更為了警醒學生利用函數圖像解題要符合實際. 另外，教師通過問題引導促使學生進行反思，出現思維沖突，產生懷疑，培養學生批判精神. 問題解決后及時引導歸納提煉，還能提升學生分析、歸納、反思的能力.

2. 開放拓展，開拓思維

問題2? 如圖2，圓柱形容器內水平放置著兩個實心圓柱體組成的“幾何體”，幾何體的下方圓柱體的底面積為15 cm2，容器的底面積為30 cm2. 現向容器內勻速注水，注水過程中，水面高度h（cm）與注水時間t（s）之間的關系如圖3所示，注滿為止.

根據圖像解答下列問題：

（1）圓柱形容器高為______cm;

（2）求勻速注水的水流速度（cm3/s）的值.

教學片段：

（利用足夠的時間讓學生自主思考后……）

師：哪位同學自告奮勇來談談你的思考過程.

生C：我觀察坐標圖的第三段末端點，題中有“注滿為止”，故14 cm就是圓柱形容器的高，但不知道水流速度的公式.？搖？搖？搖

師：分析得好. C同學，注意“cm3/s”為水流速度的單位，想到了什么？

（生C似有所悟，剛要回答，被生D急切搶答）

生D：我知道了！水流速度應該是單位時間內流出水的體積，而且第三段圖像告訴我，水流速度為=5（cm3/s）.

師：真不錯. 根據圖像，同學們還能提出可以解決的問題嗎？

（小組合作交流，學生進入思辨狀態……）

生E：可以求a的值.

師：哪位同學來回答？

生F：下方圓柱體的底面積為15 cm2，水流速度為5 cm3/s，所以18×5=a（30-15），得a=6.

生G：可以求“幾何體”上方圓柱的高.

生H：還可以求“幾何體”上方底面積S……

師：嗯，哪位同學來求一下“幾何體”上方圓柱的高和底面積S……

（學生躍躍欲試，很快就有了解決方法）

師：同學們真不簡單！下面我們來總結一下，用函數圖像來解決問題要對函數圖像進行三看：一看軸、二看點、三看線，并且要關注圖像端點與實際意義的“互譯”.

設計意圖? 發展高階思維的關鍵途徑是讓學生從“思考——分析——交流——判斷——評價——創造”的過程中，達到思維的碰撞、交流、內省. 學生出現的“不解和疑問”或“一些困惑、混淆或懷疑”引發的暫時的思維不暢通，教師就要加以疏導. 開放拓展，就是倡導學生自主學習、提出問題，并通過小組合作等形式的學習方式進行思辨、評判，讓學生體驗問題提出的多角度、多樣性，提高學生探究的積極性. 開拓思維促成學生的自我省思與策略調節，讓學生經歷綜合分析、理解反思、創造評價，這是進行探究過程的核心收獲，它將發展學生的高階思維能力.

3. 導學探究，延伸思維

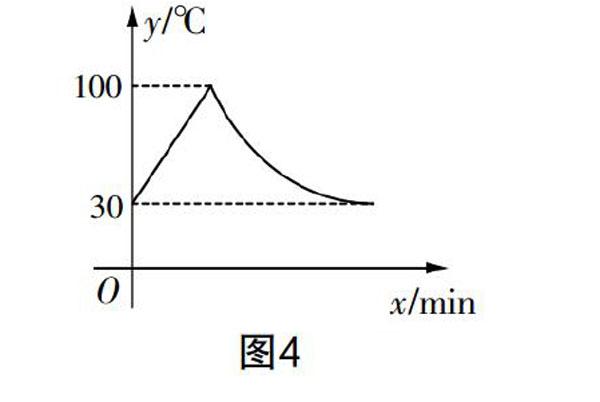
問題3? 對某教室內的飲水機開機加熱，水溫每分鐘上升10 ℃，加熱到100 ℃，停止加熱，水溫開始下降，此時水溫y（℃）與開機后用時x（min）成反比例關系，下降至30 ℃進入自動加熱階段，重復上述自動程序. 在水溫為30 ℃時，接通電源后，水溫y（℃）和時間x（min）的關系如圖4所示. 為了在上午第一節下課時（8：45）能喝到不超過50 ℃的水，則當天上午的哪個時刻可以是接通電源的時刻（？搖? ? ?）

A. 7：20 B. 7：30

C. 7：45 ?D. 7：50

教學片段：

（學生思考與操作良久，沒有頭緒，于是筆者開始導學）

師：同學們，老師接下來幫助大家進行思考，首先……

導學1：當第一次水溫為100 ℃時的該點的坐標是什么？當水溫第一次降至30 ℃時，該點的坐標是什么？

生I：開機加熱時水溫每分鐘上升10 ℃，由圖像告知100-30=70（℃），70÷10=7（min），故水溫為100 ℃時的該點的坐標是（7，100）. 從而得直線與反比例函數的解析式分別為y=10x+30與y=. 當第一次降至30 ℃時，該點的坐標是，30.

導學2：從第一次開始加熱到水溫降至30 ℃，這個過程中水溫不超過50 ℃的時間范圍是多少？大家一起小組合作交流與探究.

（經過討論，答案逐漸明朗）

生J：如圖5，水溫不超過50 ℃的時間范圍為0≤t≤2或14≤t≤.

導學3：從第一次開始加熱到水溫降至30 ℃，需要多少時間？接下來是不斷循環這個過程嗎？如果從0：00開始加熱，經過700分鐘的時刻水溫是否符合要求（不超過50 ℃）？怎么思考？大家一起小組合作交流與探究.

生K：由y=10x+30與y=可知，當第一次降至30 ℃，點的坐標為，30，得出min，為一個循環周期，700分鐘剛好為30個周期，符合要求. 但我還是不能解決原題，沒有思路.

師：好的，接下來再看看下面問題的第一問.

導學4：第一問，如果從0：00開始經過701分鐘的時刻水溫是否符合要求（不超過50 ℃）？第二問，為了在上午第一節下課時（8：45）能喝到不超過50 ℃的水，則接通電源的時間可以是當天上午的7：20嗎？

生L：明白了，701分鐘是30個周期余1分鐘，余數在0≤t≤2或14≤t≤范圍內，所以符合要求;7：20-8：45為85分鐘，85÷=3+，3個周期余個周期，×=15分鐘，符合要求，故選A.

師：真棒！其實第三小問與第二小問的區別就在題中的條件“重復自動程序”（周期），那么用圖像來刻畫，我們只要畫一條直線y=50， 關注圖像中的交點與該線上方與下方，顯然這些在直線 y=50 的下方的圖像對應的都是水溫不超過 50 ℃. 所以，函數圖像中的交點與線上、線下能告訴我們解決問題的思路. 同學們，還有其他方法嗎？課外試一下……

設計意圖? “問題導學”是以核心問題為主線，解決問題為基石，引領學生在發現問題、生成問題、解決問題過程中掌握知識、技能、方法，形成自主學習能力，激發學習數學興趣，促進學生高階思維發展. 通過問題導學，以問題解決為重心、師生圍繞“導學問題”而開展自主合作探究學習為主要特征的思維課堂充分得以開展. 本環節中的4個導學問題為學生解決問題而導，核心是“學”，關鍵在“導”. “問題導學”有效性不僅需要教師關注如何創設“問題”，引領學生解決問題，還要關注如何啟發學生發現問題，表達自己的困惑，讓學生也能提出“問題”，真正使問題引導學習，問題驅動學習. 導學探究，能加大思維延伸力度，使課堂教學指向高階思維.

4. 變式評價，創造思維

問題4? 如圖6，甲在離地2米的A處將排球發出，球沿著拋物線的一部分運行，當球運行到離他站立地方的水平距離為6米的地方時達到最高高度h米. 已知球網與發球點O的水平距離為9米，高度為2.27米，球場對面的邊界距O點的水平距離為18米，以點O為原點，OA所在直線為y軸建立直角坐標系，當h=3的時候，球能過網嗎？請說明理由.

教學片段：

（有了前面的教學，學生很快有了解決問題的辦法）

生M：根據題意，h=3，設該拋物線為y=a（x-6）2+3，且過點（0，2），得出拋物線y=-（x-6）2+3 . 取x=9，代入拋物線方程得y=2.75，大于2.27，故球能過網.

師：嗯，不簡單. 題干不變，對問題進行如下變式.

變式1：若球一定能越過球網，求h的取值范圍.

生N：根據題意，設該拋物線為y=a（x-6）2+h，且過點（0，2），得出a=，拋物線為y=（x-6）2+h. 取x=9，代入得y=（9-6）2+h>2.27，故h>2.36.

變式2：若球既能越過球網，又不出邊界，求h的取值范圍. （小組合作交流）

生O：在h>2.36的情況下，y=·（x-6）2+h，取x=18代入y=（18-6）2+h<0.

生P：不對！應該是y=（18-6）2+h≤0，解得h≥，在h>2.36的情況下，h的取值范圍為h≥.

變式3：在實際情況下，人發球后球的飛躍最高點不會超過8米，要求球既能越過球網，又不出邊界，則人應該在何處發球？（課后研究）

……

設計意圖? 變式是數學的魔方，變式是創新的訓練場. 變式促進交流與評價，是一種再創造，帶領學生在解決問題的過程中培養高階思維. 美國著名數學家波利亞就指出：發展學生的解決問題的能力是數學教育主要目的之一，尤其是在變換不同背景下的問題理解與分析能力. 其實變換不同背景就是“變式”. 改變就題論題的課堂，促進學習者通過變式解決問題能力的表現，已經成為學生創新能力強弱的標準之一，應該得到數學教育工作者的高度重視. 另外，課堂的延伸需要引導學生進行課后研究，給出一個變式讓學生在函數圖像環境中繼續探究，讓學生對問題解決方法的再認識和再創造，也是高階思維的培育的手段之一.

問題驅動下指向高階思維的思考

1. 問題驅動、問題選擇與創設是前提

問題驅動是以學生為主體、以選擇與創設的問題為學習起點，圍繞問題解決推動學習內容，讓學生在問題尋求解決方案的同時提升思維能力. 心理學家指出，“問題”是思維活動進行的原動力和牽引力. 葉瀾教授曾提到“驅動學生思維的有效載體是好的數學問題，新基礎教育成功的關鍵指標之一是老師們關注數學課堂教學過程中的問題設置”. 為了讓學生更好地回顧舊知、更好地發展數學高階思維、更好地完善自我學習品質，就應該選擇與創設“好的數學問題”. 所以我們說，初中數學專題課堂都有它的知識呈現與生成、數學思維訓練以及價值體現，這些都需要問題驅動. 數學課堂是問題的課堂，是有效學習的課堂. 正是這樣，選擇與創設數學問題是非常關鍵的，對于學生來說，需要的是有效的問題驅動，一堂有效的數學課堂教學，一定是有效問題組合體的進行曲.

2. 高階思維，過程啟發與引導是關鍵

高階思維能力的培養是一個過程，要通過學生產生同感、共情、猜想、探索、批判、思辨、創新、評價來展現高階思維. 它的行為表現也往往需要學生在問題理解與問題分析、策略探求、猜想比較、結論判斷、后期驗證的基礎上更深層次地對知識理解、推廣與運用，這需要教師的啟發與引導. 由于問題驅動就是“問題教學”，“問題教學”的基礎在于思維活動的啟發與引導. 因此，教師就是思維的“喚醒者”，喚醒的過程就是學生思維能力不斷提升的過程，伴隨著高階思維能力的發展. 本案例教學證明，通過啟發與引導助力問題解決、利于學生思維生長.

3. 專題課堂，注重內化與反思是期待

在專題課的教育教學中，教師要注重內化與反思，舍得留出一定時間讓學生大膽嘗試解決問題，適時引導，期待找到問題的核心內容與方法所在，挖掘思維深度. 這需要進行學習方式的變革，提倡探究式、問題解決式、自主學習、合作交流等學習方式. 特別是探究式，因為探究嘗試的過程，就是發展高階思維的過程. 解決問題后應留時間讓學生進行內化，因為內化的過程，就是自我提升的過程，要將探究策略與經驗內化為自己的數學素養. 學生學習能力發展是專題課的著眼點，讓學生通過課堂學習，創新數學思維方式，積累解決問題的方法，并不斷進行反思. 反思是一種學習品質，它將促成優化意識的提升[3].

高階思維能力的培養是細水長流、潛移默化的過程. 本文僅僅以“函數圖像會說話”的專題教學為例，在問題驅動下指向高階思維的課堂實踐進行了一次整理與反思，希望起到拋磚引玉的作用，期待更多的數學教育教學工作者進一步深入研究.

參考文獻：

[1]任樟輝. 數學思維理論[M]. 桂林：廣西教育出版社，2003.

[2]林崇德，胡衛平. 思維型課堂教學的理論與實踐[J]. 北京師范大學學報（社會科學版），2010（01）.

[3]夏培培. 以問題為“驅動”發展學生數學高階思維能力——以“幾何最值問題”的專題探究為例[J]. 中學數學，2019（06）.