基于預估校正的改進準靜態方法的中子動力學計算研究
賀濤 李云召 張文鑫 王冬勇 馬黨偉

摘 要
早年,堆芯瞬態分析常采用簡化的“點堆”動力學模型,不考慮瞬態過程中堆芯中子通量密度隨空間的分布,且不隨時間變化。“點堆”動力學模型求解快速,對小型緊湊耦合系統在一定情況下可給出較滿意結果,但由于其無法描述與空間相關的擾動過程。然而,大型商用壓水堆的瞬態分析中,特別是事故工況下,中子通量密度空間分布隨時間變化會非常劇烈,點堆模型在這種情況下的近似非常大。因此,為了精確模擬大型壓水堆的瞬態過程中,中子通量密度分布隨時間的變化過程,必須采用三維的時空動力學模型。本文使用預估校正的改進準靜態方法求解時空動力學方程,并于基準題對比,驗證了預估校正的準靜態方法計算的正確性。
關鍵詞
中子動力學方程;基于預估校正的改進準靜態方法
中圖分類號: TL327 ? ? ? ? ? ? ? ? ? ? 文獻標識碼: A
DOI:10.19694/j.cnki.issn2095-2457 . 2020 . 17 . 10
0 前言
三維時空中子動力學方程組的求解需要進行時間變量的離散。傳統的時間離散方法為差分離散,分為包括隱式差分、顯示差分以及半隱式差分。差分方法的理論模型簡單,典型的程序實現包括NESTEL[1],PARCS[2],SIMTRAN等。但是,若要保證計算的精度,差分離散的時間步長需要嚴格限制在比較小的數量級,這就導致堆芯擴散計算的次數大量增加。
同時,在20世紀50年代,有學者提出了準靜態的思想,即將中子通量密度的形狀與幅度隨時間的變化分開計算。在堆芯中,中子通量密度的形狀隨時間變化較為緩慢,因此可以在較大的時間步長上進行求解;而中子通量密度的幅度隨時間變化迅速,同時幅度的計算耗時較小,因此可以在較小的步長上進行計算。K.O. OTT與Henry A.F.在此基礎上,提出了改進準靜態方法。即將中子通量密度與先驅核濃度因式分解為形狀函數與幅函數,并且引入歸一化條件保證因式分解的唯一性。然而研究發現,由于在計算過程中,為了保證瞬態過程中形狀函數與幅函數始終滿足歸一化條件,必須在計算步長上迭代形狀函數與幅函數。而形狀函數的求解仍是中子的擴散計算,耗時巨大,使改進準靜態方法的計算效率極其低下。為了解決改進準靜態方法中,迭代形狀函數與幅函數使計算效率低下的問題,Sandra Dulla在改進準靜態方法的基礎上提出了預估校正策略,去掉了迭代形狀函數與幅函數的步驟,提高了計算效率。
1 中子擴散時空動力學方程組
上述兩式是一個常微分方程組,和通常的點堆方程形式上是一致的,區別在于此處方程中的變量和系數是形狀函數、共軛通量以及截面參數等的積分比值量。
3 程序開發與應用分析
本文采用面向對象的模塊化FORTRAN95語言研發了三維時空動力學計算程序Bamboo-Transient。
本文采用三維LMW基準題對程序進行驗證。
3.1 三維LMW基準題簡介
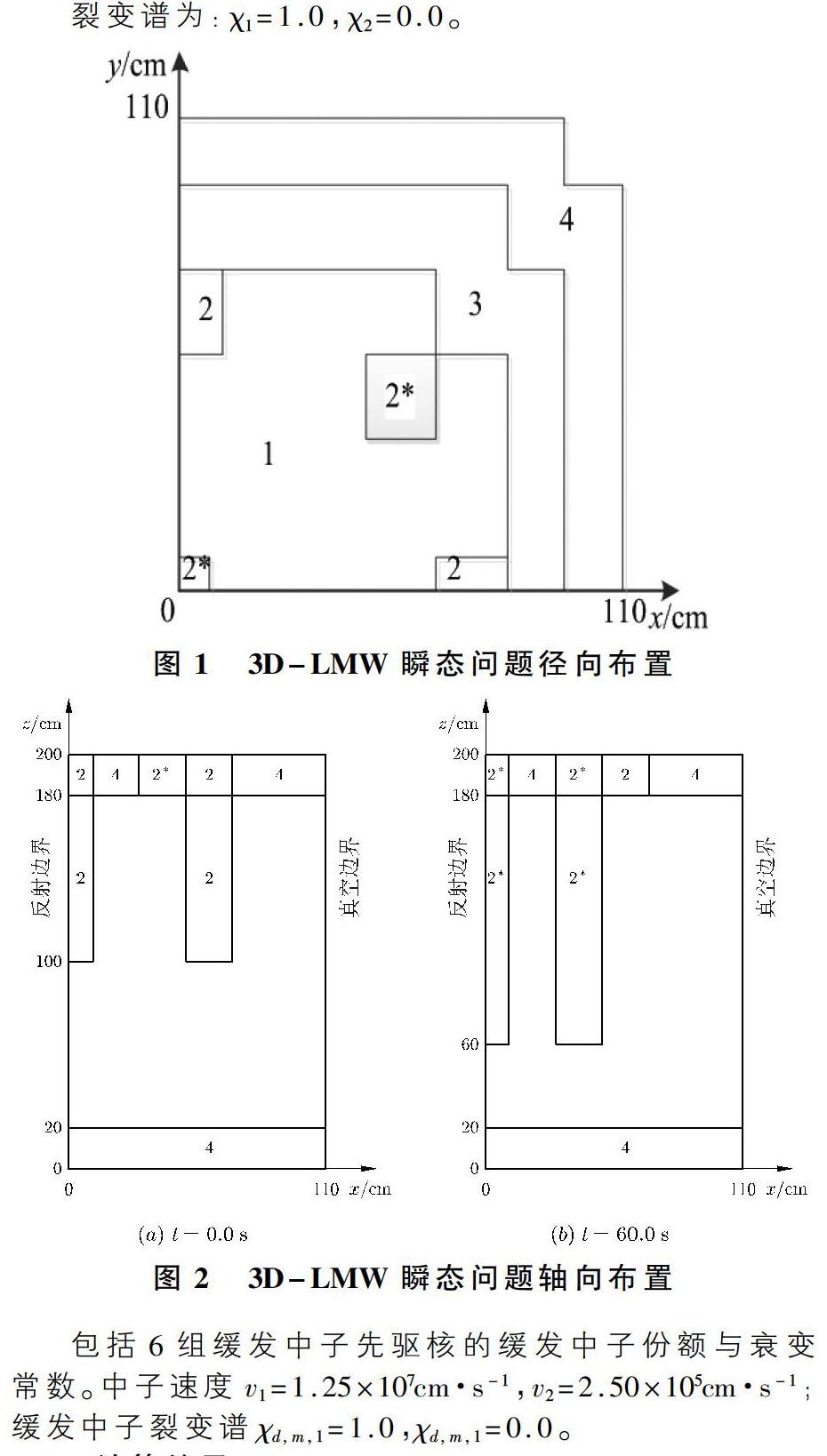
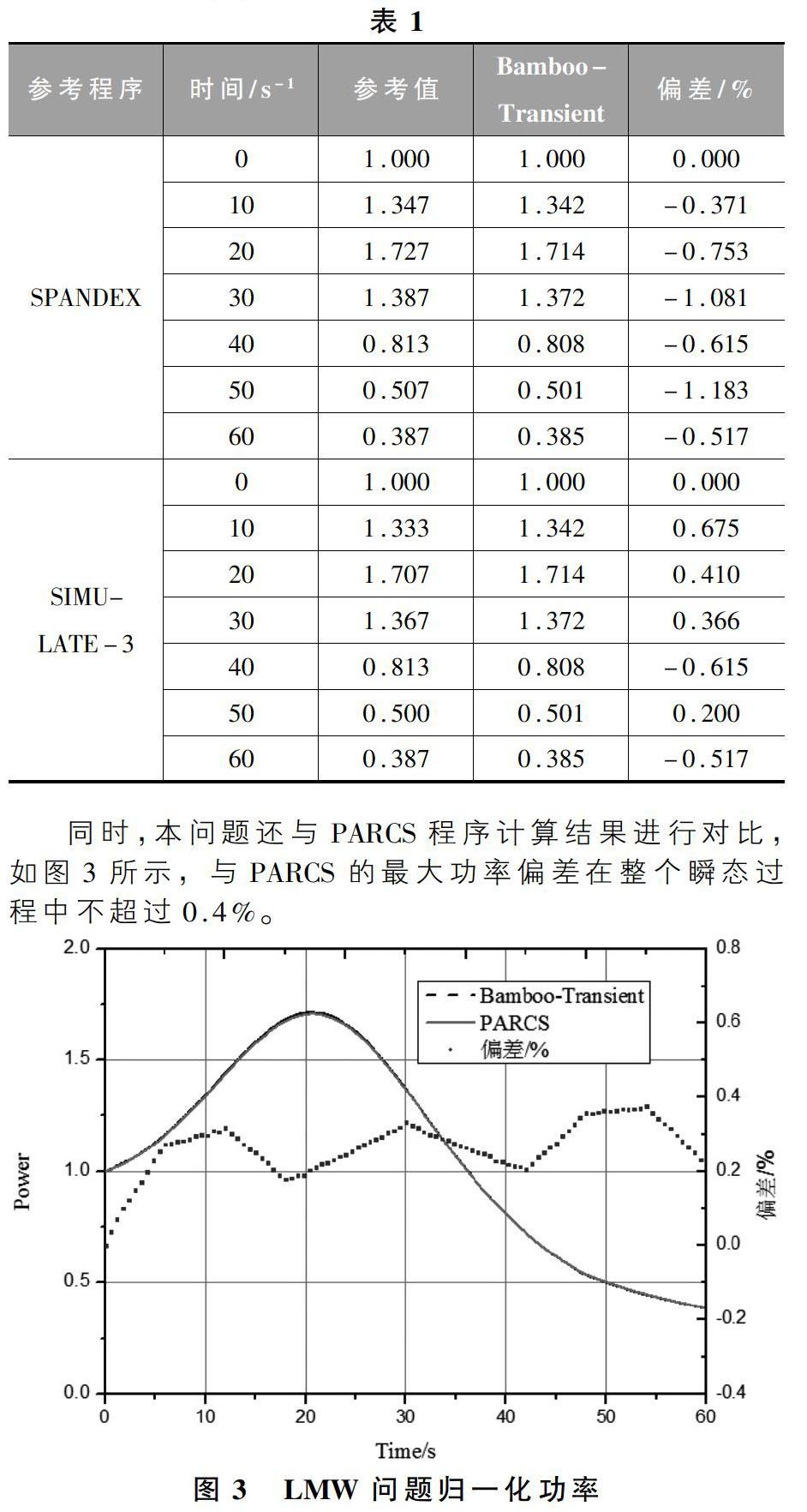
該動力學問題是三維兩群穩態LMW問題的拓展,包含六組緩發中子動力學參數,外邊界條件為真空邊界,瞬態過程起始(t=0.0s)和終止(t=60.0s)時刻的軸向布置分別如圖2所示。瞬態過程由堆內的兩組控制棒軸向運動引起:瞬態開始前,第一組控制棒(材料標號為2)插入至堆芯中部100cm處,第二組控制棒(材料標號為2*)提出活性區外;從0.0s到26.666s間,第一組控制棒以3.0cm/s的速度提出堆芯活性區,從7.5s至47.5s間第二組控制棒逐漸插入堆芯60cm處。
各材料的截面參數和動力學參數分別列于基準題中共4種材料,在堆芯中的布置如圖1所示。各種材料的宏觀截面參數由基準題給出,列于表3中,包括兩群的擴散系數、宏觀吸收截面、宏觀裂變截面與散射截面。
裂變譜為:χ1=1.0,χ2=0.0。
包括6組緩發中子先驅核的緩發中子份額與衰變常數。中子速度v1=1.25×107cm·s-1,v2=2.50×105cm·s-1;緩發中子裂變譜χd,m,1=1.0,χd,m,1=0.0。
3.2 計算結果
問題中的組件大小為20cm×20cm,每個組件被劃分為超過10個的計算網格。控制棒材料的吸收作用在此問題中非常弱,瞬態過程中的功率水平和通量形狀的變化非常緩慢,因此可以采用較大的時間步長,整個瞬態過程持續60s,總共更新60次形狀函數。本問題采用兩組參考值,均是由節塊擴散程序得到。兩種計算模型得到的歸一化功率水平和兩組參考值均符合得較好,和SPANDEX程序的最大偏差為-1.183%,和SIMULTATE-3程序的最大偏差為0.675%。
同時,本問題還與PARCS程序計算結果進行對比,如圖3所示,與PARCS的最大功率偏差在整個瞬態過程中不超過0.4%。
4 結論
本文推導了基于預估校正的準靜態方法的中子動力學計算模型,在Bamboo-Transient程序中進行了應用,并選取LMW基準題對該方法進行了驗證分析,計算結果與國際上同類程序相當。
參考文獻
[1]Turinsky P J. NESTLE: Few-group neutron diffusion equation solver utilizing the nodal expansion method for eigenvalue, adjoint, fixed-source steady-state and transient problems[R].North carolina State University, 1994.
[2]Downar T, Xu Y, Seker V. Theory Manual for the PARCS Kinetics Core Simulator Module[R].University of Michigan, 2010.

