橡膠超彈性測試及其對輪胎有限元計算結果的影響

付新華，李 寧，郭淵昊，李 鵬

（三角輪胎股份有限公司，山東 威海 264200）

輪胎在接地時變形較復雜，受壓縮、剪切及拉伸等多種變形共同影響，目前有限元分析一般采用基于單軸拉伸數據擬合的Yeoh或Neo-Hookean等超彈性模型進行表征[1-2]。本工作以實際測試數據及超彈性擬合數據分析研究這種表征方式的適用性及其與綜合拉伸＋剪切＋壓縮試驗數據擬合得到的超彈性本構模型的精度差異。

1 試驗測試

橡膠材料幾乎不可壓縮，因此一般用單軸拉伸、等雙軸拉伸和平面拉伸等變形模式來表征橡膠材料的單軸拉伸/壓縮、等雙軸拉伸/壓縮及平面拉伸/壓縮等力學特性。

對某規格全鋼子午線輪胎膠料進行單軸拉伸、等雙軸拉伸和平面拉伸3種變形模式的測試，試驗夾具如圖1所示。將試驗數據進行處理，得到3種變形模式的應力-應變曲線，并與擬合結果進行對比。

圖1 試驗夾具

2 不同變形模式試驗結果擬合

目前有多種本構模型可以表征橡膠材料的超彈特性，除了上述兩種模型外，還有基于熱力學統計的Van der Waals模型和Arruda-Boyce模型及基于現象學的完全多項式模型和Ogden模型等。總體而言，基于變形張量I1的模型包括Neo-Hoohean和Yeoh等縮減多項式模型、Marlow模型和Van der Waals模型（β＝0，β為變形張量I1和I2合成I的線性參數）；基于I1和I2的模型包括Ogden模型和Van der Waals模型（β≠0）。這些模型的適用范圍和擬合精度不同。下面以同種膠料試驗為例研究不同變形模式組合時幾種常用本構模型的擬合精度[3-4]。

2.1 單軸拉伸數據擬合

單軸拉伸數據擬合的Yeoh，Ogden和Van der Waals模型的應力-應變曲線與試驗結果的對比分別如圖2—4所示。由圖2—4可以得出以下結果。

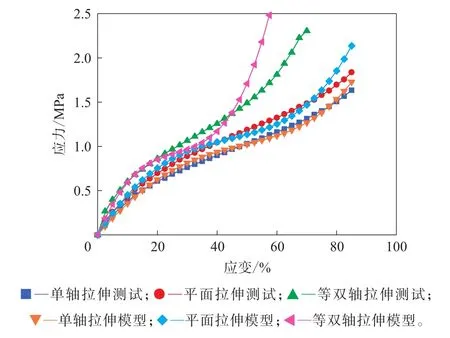
圖2 單軸拉伸數據擬合的Yeoh模型的應力-應變曲線與試驗結果的對比

單軸拉伸數據擬合得到的Yeoh模型表征的單軸拉伸曲線與測試數據匹配較好，平面拉伸變形擬合精度也較高，而等雙軸變形模式下應變小于50%時也相對合理。

Ogden模型擬合出的單軸拉伸曲線與測試數據擬合較好，但另外兩種變形模式與測試數據差別巨大，因此僅有單軸拉伸數據時不適宜用Ogden本構模型。

Van der Waals模型擬合出的單軸拉伸曲線與測試數據擬合較好，而另外兩種變形模式與測試數據差別很大。

由此可見，在僅有單軸拉伸測試數據時，Ogden和Van der Waals模型的擬合精度不如Yeoh模型。

2.2 單軸拉伸＋等雙軸拉伸數據擬合

單軸拉伸＋等雙軸拉伸數據擬合的Yeoh，Ogden和Van der Waals模型的應力-應變曲線與試驗結果的對比如圖5—7所示。由圖5—7可得出以下結果。

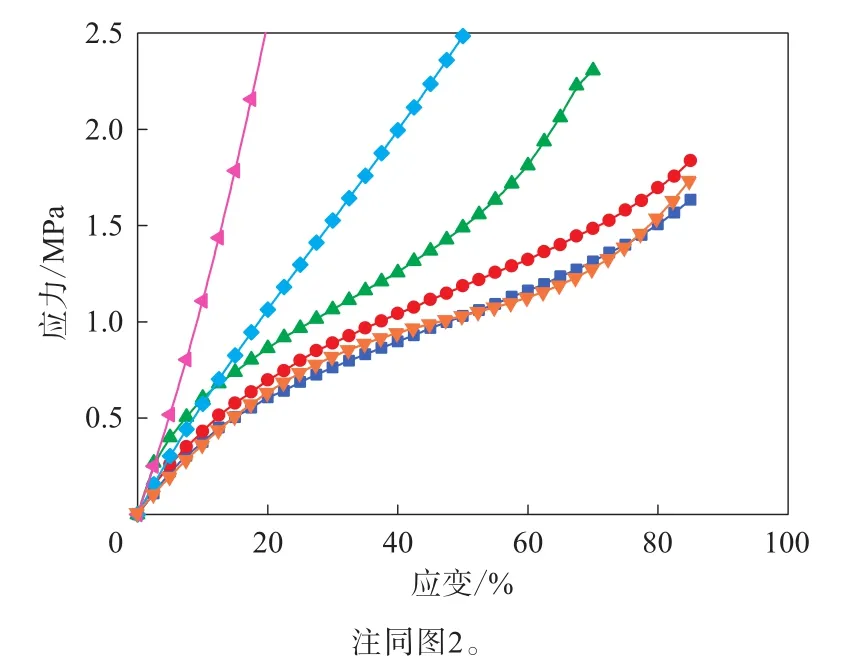
圖3 單軸拉伸數據擬合的Ogden模型的應力-應變曲線與試驗結果的對比

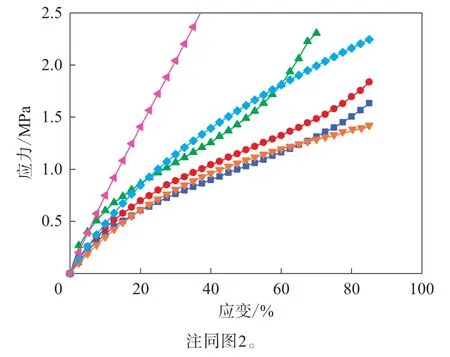
圖4 單軸拉伸數據擬合的Van der Waals模型的應力-應變曲線與試驗結果的對比

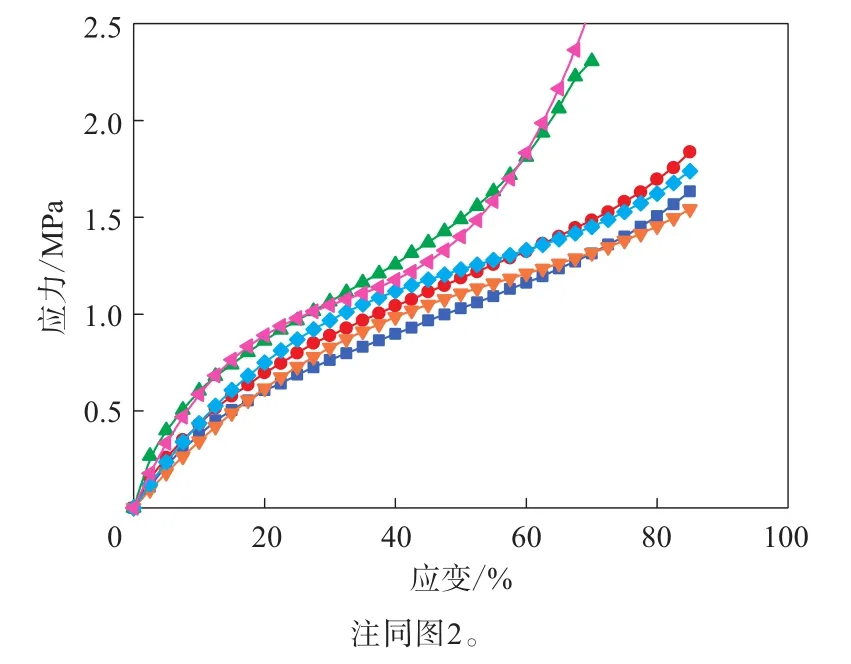
圖5 單軸拉伸＋等雙軸拉伸數據擬合的Yeoh模型的應力-應變曲線與試驗結果的對比

通過單軸拉伸＋等雙軸拉伸數據擬合Yeoh模型表征的等雙軸變形模式曲線的精度比僅有單軸拉伸數據時得到很大提升。

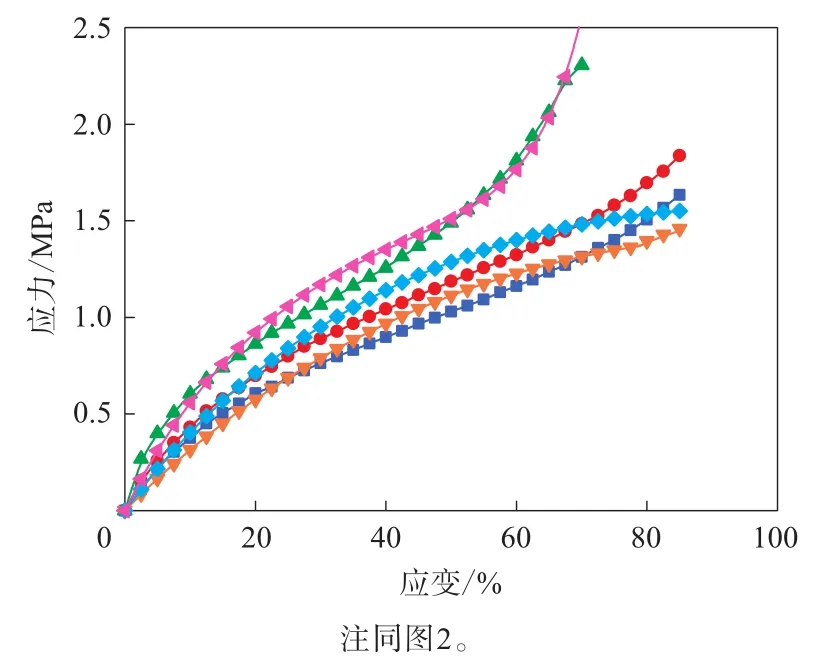
圖6 單軸拉伸＋等雙軸拉伸數據擬合的Ogden模型的應力-應變曲線與試驗結果的對比

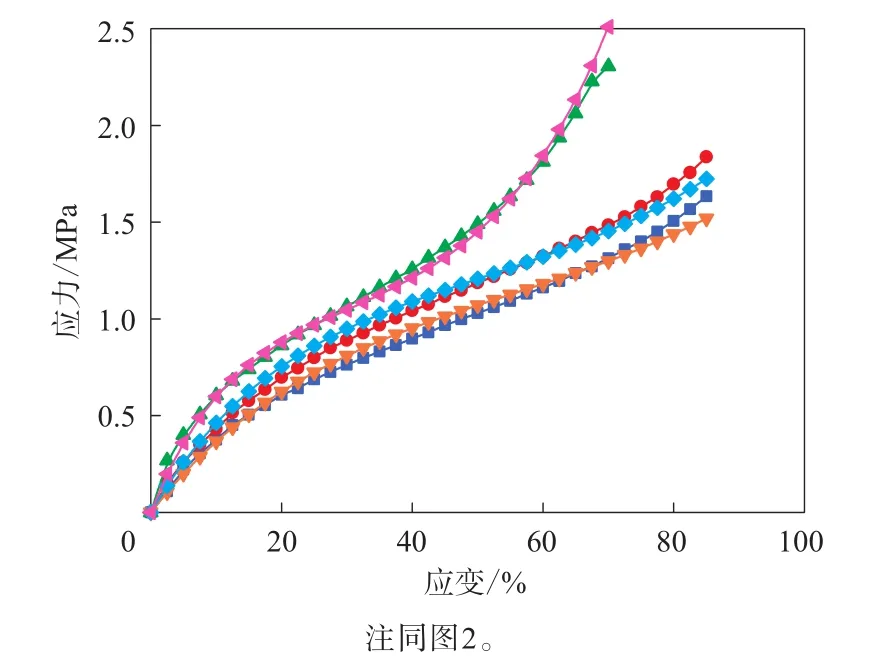
圖7 單軸拉伸＋等雙軸拉伸數據擬合的Van der Waals模型的應力-應變曲線與試驗結果的對比

通過單軸拉伸＋等雙軸拉伸數據擬合Ogden模型表征的單軸拉伸和等雙軸拉伸變形模式曲線與測試數據擬合較好，但平面拉伸變形模式曲線與測試結果仍有差別。

通過單軸拉伸＋等雙軸拉伸數據擬合Van der Waals模型表征的3種變形模式曲線與測試數據擬合精度較高。

2.3 單軸拉伸＋平面拉伸數據擬合

單軸拉伸＋平面拉伸數據擬合的Yeoh，Ogden和Van der Waals模型的應力-應變曲線與試驗結果的對比如圖8—10所示。由圖8—10可見以下結果。

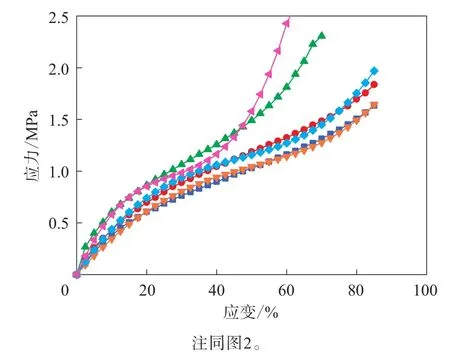
圖8 單軸拉伸＋平面拉伸數據擬合的Yeoh模型的應力-應變曲線與試驗結果的對比

通過單軸拉伸＋平面拉伸數據擬合Yeoh模型表征的單軸拉伸和平面拉伸變形模式曲線與測試結果擬合非常好，等雙軸變形模式曲線擬合精度也比僅有單軸拉伸測試數據時得到提升。

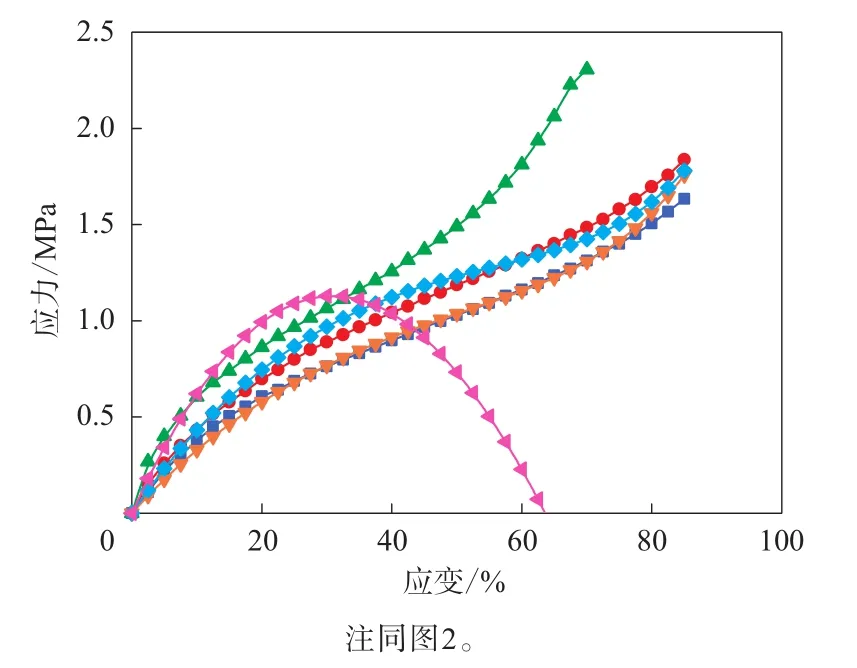
圖9 單軸拉伸＋平面拉伸數據擬合的Ogden模型的應力-應變曲線與試驗結果的對比

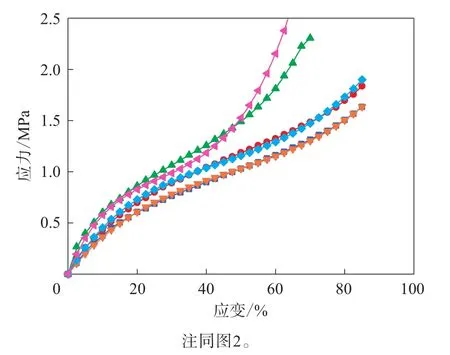
圖10 單軸拉伸＋平面拉伸數據擬合的Van der Waals模型的應力-應變曲線與試驗結果的對比

通過單軸拉伸＋平面拉伸數據擬合Ogden模型表征的單軸拉伸和平面拉伸變形模式曲線與測試結果擬合非常好，但等雙軸變形模式曲線與測試結果差別巨大。

通過單軸拉伸＋平面拉伸數據擬合Van der Waals模型表征的單軸拉伸和平面拉伸變形模式曲線與測試結果擬合度非常高，但等雙軸變形模式曲線與測試數據仍有差距。

2.4 單軸拉伸＋等雙軸拉伸＋平面拉伸數據擬合

單軸拉伸＋等雙軸拉伸＋平面拉伸數據擬合的Yeoh，Ogden和Van der Waals模型的應力-應變曲線與試驗結果的對比如圖11—13所示。

由圖11—13可見，通過3種變形模式數據擬合的Yeoh，Ogden和Van der Waals模型表征的單軸拉伸、平面拉伸和等雙軸拉伸變形模式曲線與測試結果的擬合度均非常高。

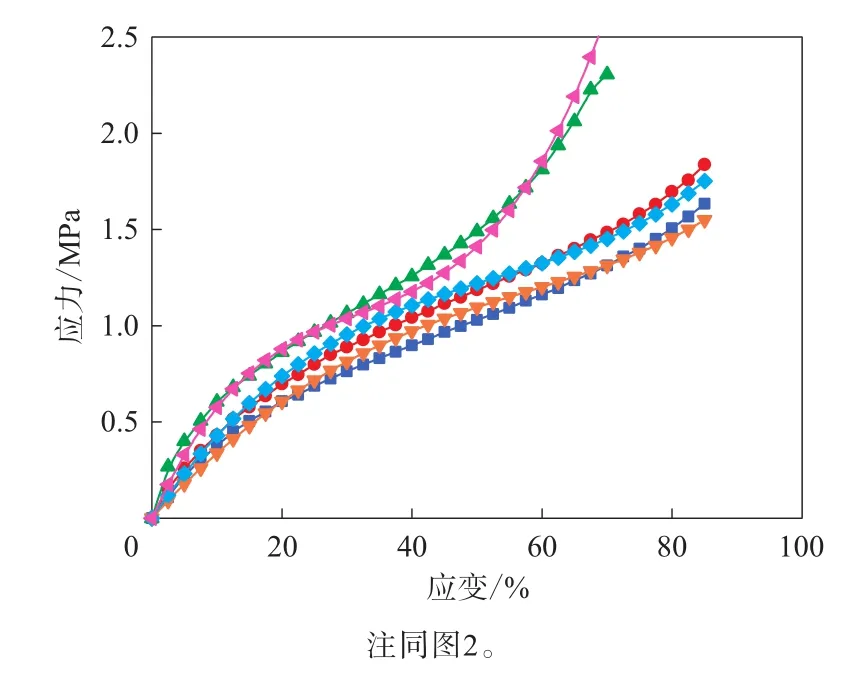
圖11 3種變形模式測試數據擬合的Yeoh模型的應力-應變曲線與試驗結果的對比

通過對Yeoh，Ogden和Van derWaals超彈性本構模型在不同變形模式試驗數據下的擬合結果對比可以得到以下結論。

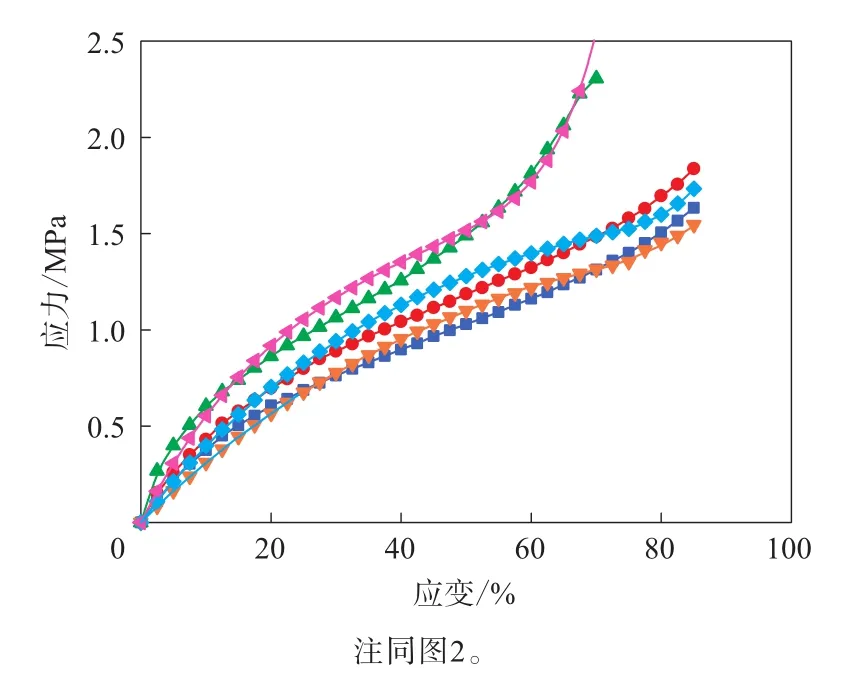
圖12 3種變形模式測試數據擬合的Ogden模型的應力-應變曲線與試驗結果的對比

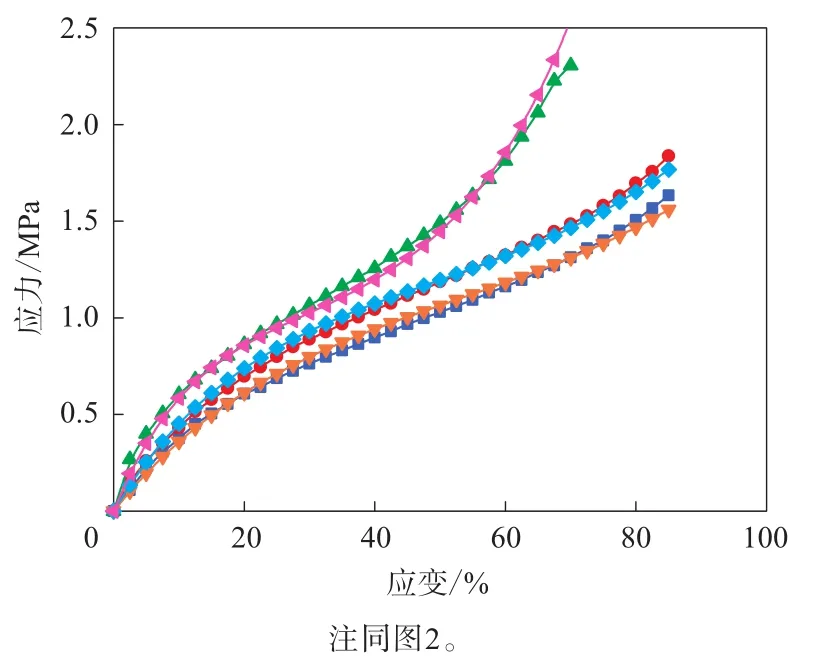
圖13 3種變形模式測試數據擬合的Van der Waals模型的應力-應變曲線與試驗結果的對比

（1）Yeoh模型隨變形模式匹配擬合精度波動較小，因此僅有單軸拉伸數據時適宜用Yeoh模型。

（2）Ogden模型對任意一種或者幾種變形模式的擬合精度都很高，也可以說該模型擬合時只對輸入的變形模式的試驗數據的精度負責，而其他變形模式則可能非常差，因此該模型適用于擬合變形模式全面的試驗數據。

（3）等雙軸拉伸試驗數據是Ogden和Van der Waals模型擬合精度的關鍵，因為該變形模式表征膠料壓縮特性，結合輪胎實際運動變形情況，仿真時所用本構模型最好能夠表征等雙軸拉伸變形。

（4）上述各本構模型對不同膠料的擬合精度也不盡相同，一方面與材料本身性能有關，同時對測試精度也有很高的要求。

3 仿真驗證

以相同規格全鋼子午線輪胎為例驗證不同變形模式下的計算精度以及3種變形模式下Yeoh，Ogden和Van der Waals等模型的計算精度。具體驗證思路如下。

（1）選單軸拉伸及單軸拉伸＋等雙軸拉伸＋平面拉伸變形模式下結果進行變形模式對比。

（2）在單軸拉伸＋等雙軸拉伸＋平面拉伸變形模式下對Neo-Hookean，Yeoh，Ogden和Van der Waals等本構模型進行對比。

3.1 局部受力對比

選擇不同變形模式下的各本構模型進行標準負荷下的穩態滾動計算，并分別選擇帶束層端點和胎體反包端點區域的計算結果進行對比。

3.1.1 帶束層端點

帶束層端點區域受力分析見圖14，提取其應變能密度和應變數據進行分析，結果如圖15和16所示。

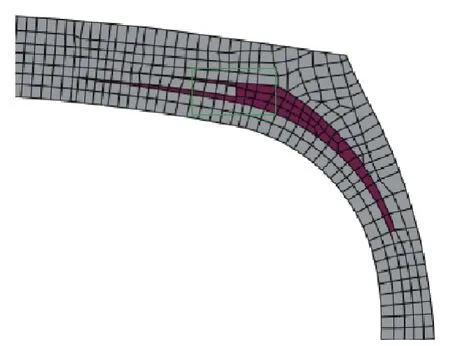
圖14 帶束層端點區域受力分析

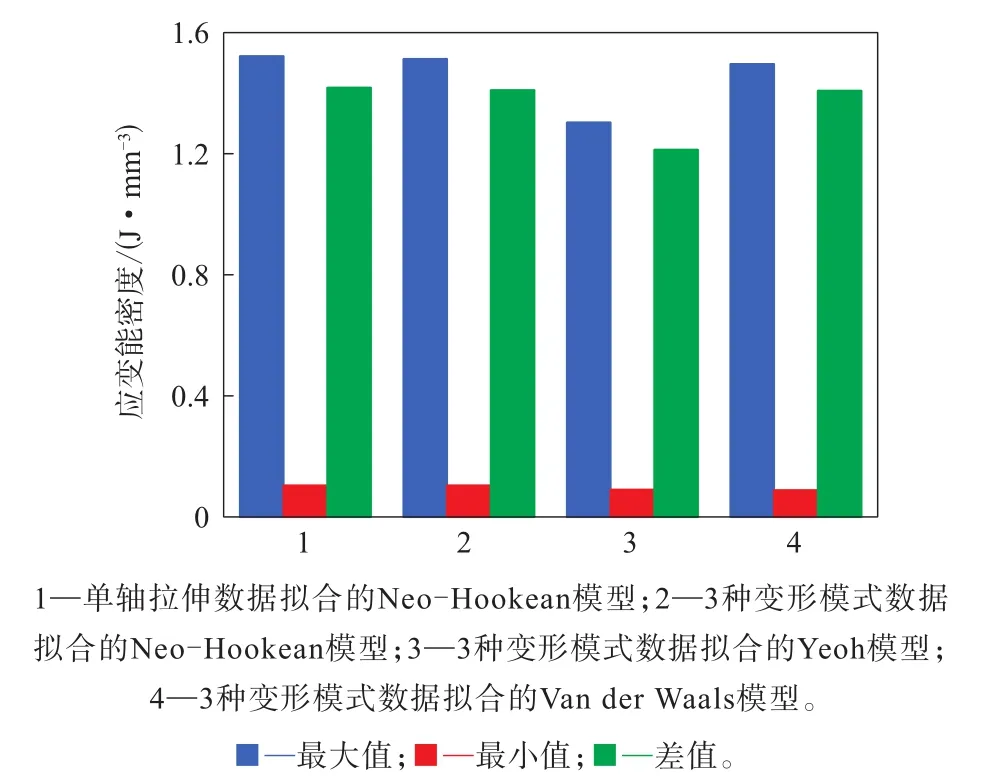
圖15 帶束層端點應變能密度幅值對比

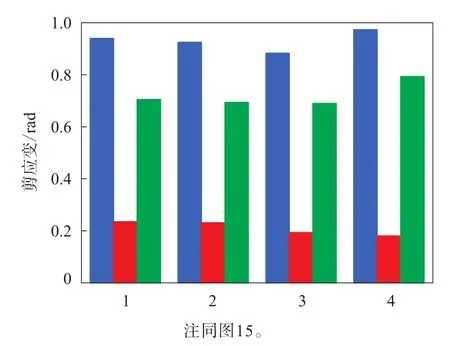
圖16 帶束層端點剪應變幅值對比

由圖15和16可見：應用不同變形模式擬合的同一本構模型帶束層端點應變能密度和剪應變計算值的變化在3%～10%范圍內；3種變形模式下不同本構模型計算值的變化在7%～15%范圍內；Yeoh與Van der Waals模型計算值的最大差異約為8%。

3.1.2 胎體反包端點

胎體反包端點區域受力分析見圖17，提取其應變能密度和應變數據進行分析，結果如圖18和19所示。

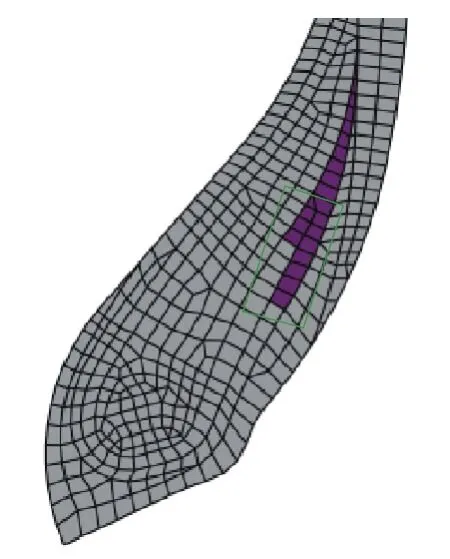
圖17 胎體反包端點區域受力分析

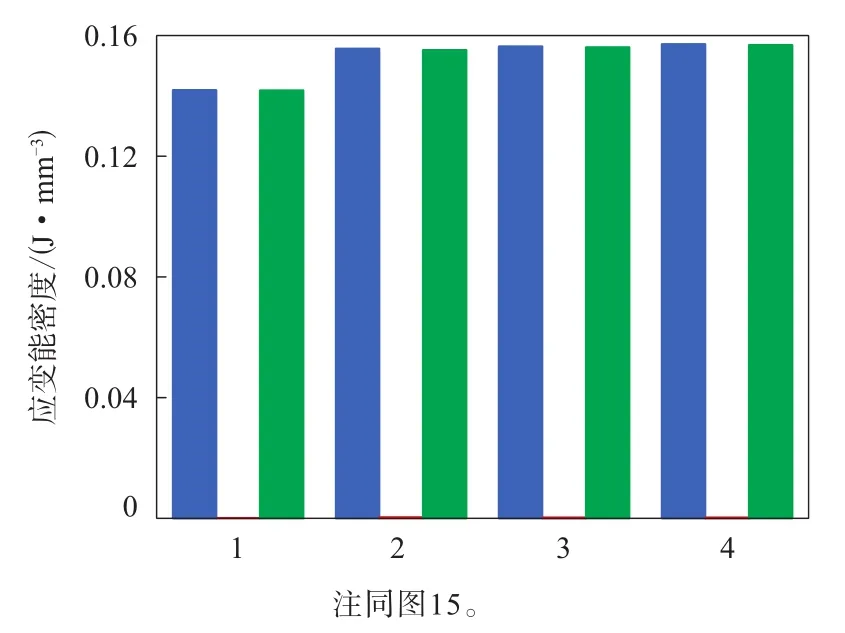
圖18 胎體反包端點應變能密度幅值對比

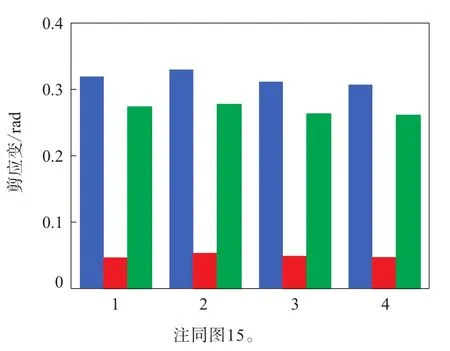
圖19 胎體反包端點剪應變幅值對比

由圖18和19可見：應用不同變形模式擬合的同一本構模型反包端點應變能密度和剪應變計算值的變化在9%～15%范圍內；3種變形模式下不同本構模型計算值的變化在2%～13%范圍內；Neo-Hookean與Van der Waals模型計算值的差異超過10%。

3.2 計算效率對比

對選用不同本構模型計算時的收斂情況及計算時間進行統計，結果如表1所示。

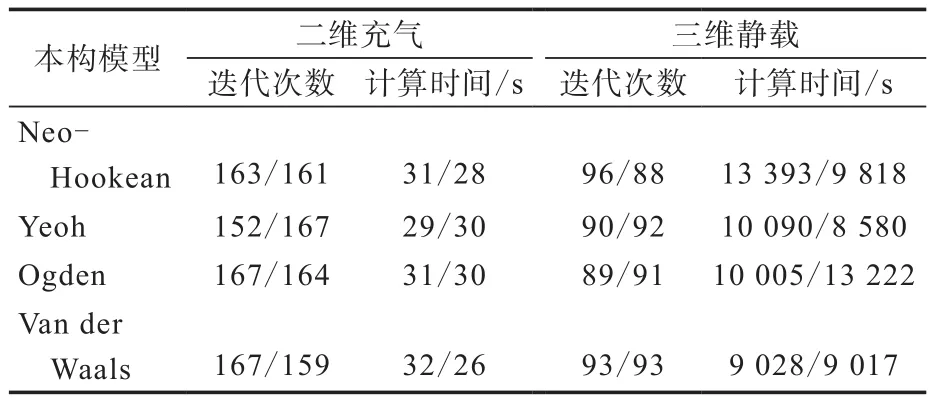
表1 不同本構模型計算時間統計

由表1可見：4種模型對兩種膠料計算的迭代次數變化趨勢不同，但各本構模型迭代次數差別不明顯；不同模型對兩種膠料的計算時間變化趨勢也不相同，Yeoh和Van der Waals模型計算時間相對較短。

該結果僅是基于一款輪胎模型在只有超彈性表征下靜載計算得到的，以說明不同本構模型在輪胎模擬計算中的區別。當輪胎模擬中同時涉及超彈性和粘彈性時需注意選擇超彈性本構模型。

4 結論

通過對不同變形模式組合下Yeoh，Ogden和Van der Waals等本構模型擬合精度的分析，得到下述結論。

（1）當僅有單軸拉伸數據時適宜選擇Yeoh模型，而用單軸拉伸＋等雙軸拉伸＋平面拉伸3種變形模式數據能夠更好地表征膠料在實際工況下的變形狀態。

（2）在測試數據包括3種變形模式時，Van der Waals和Ogden模型的擬合精度相對較高，應用擬合精度較高的模型進行計算可以更好地表征輪胎各工況的實際受力狀況，尤其是分析不同設計方案輪胎胎體反包端點和帶束層端點等局部受力時能得到更準確的結果。

此外，當模型中涉及膠料的粘彈性時還要考慮超彈性與粘彈性的匹配問題。