超聲波流量計雜質對測量精度影響機理分析

張 蒙 杜廣生 程 浩 楊 悅

(山東大學能源與動力工程學院， 濟南 250061)

0 引言

工業裝備是現代農業的硬件支撐，隨著現代工業化的發展，農業生產的各個環節和過程逐步由動力機、水利灌溉設備、耕整機、溫度控制系統、自動化噴淋裝置等農業裝備取代。超聲波流量計量程范圍廣、測量精度高，具有良好的溫度適應性，在農業灌溉、水利運輸、溫度控制、液位監測、自動化配料等領域得到廣泛應用[1-3]。隨著農業機械化技術標準要求越來越嚴格，對超聲波流量計的精度和穩定性要求也變得更高[4]。

為提高超聲波流量計的計量精度，研究者從不同角度出發，嘗試了很多技術手段。檀盼龍等[5]針對高黏度流體在輸送過程中流動狀態容易受到管道變化影響的問題，提出了一種利用遺忘因子的最小二乘法進行積分權重系數優化的方法，降低了超聲波流量計對高黏度測量的影響。張皎丹等[6]基于Gauss-Jacobi積分方法，提出了基于實際管路流態分布的數值積分優化方法，通過單彎頭理論模型和實流實驗分別進行了驗證。王鑒釗[7]針對漿液循環泵管道流量測量問題，根據超聲波信號特性的分析以及常見頻譜細化方法的選擇，將Zoom-FFT作為系統頻譜分析的方法。呂美高[8]采用離散項模型對主管道內含雜質污水的運動進行了仿真，研究了大雷諾數下雜質對流量系數k的影響。SHI等[9-10]采用實驗和數值模擬相結合的方法，分析了不同類型的雜質對V型聲道布置下超聲波信號的影響。為了探究傳播介質對超聲波信號的影響，陳志賢[11]測量了CaCl2溶液內超聲信號橫向和縱向衰減，通過實驗發現，超聲波可促進Ca(HCO3)2溶液結晶形成水垢。

相關研究表明，當超聲波流量計安裝在供熱管道上，根據供熱采暖系統水質及防腐技術要求，建筑物熱力入口的供水干管上宜設置兩級過濾器[12-13]，其中，初級為濾徑3 mm的過濾器，二級為濾徑0.65～0.75 mm的過濾器。對于分戶熱計量的住宅，流量計宜設在回水管上，進入流量計前的回水管上應設過濾器，濾網規格不宜小于0.25 mm(60目)[14]。由于含雜質水流屬于非均勻介質，雜質的成分、大小、分布、在水中所占體積分數都會對測量信號產生影響，因此，對流量計內含雜質水流的研究非常必要。本文采用數值模擬計算和實驗研究相結合的方法，研究雜質顆粒粒徑在不同流量下對超聲波流量計測量精度的影響，以提升超聲波流量計的精度和適用性。

1 含雜質水流的超聲波傳播數值模擬

1.1 數學模型

液相采用標準k-ε模型[15-19]，k方程為

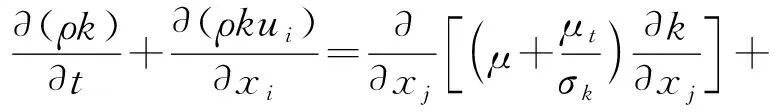
(1)

ε方程為

(2)

式中Gk——由平均速度梯度所產生的紊流動能

Gb——由浮力產生的紊流動能

YM——引起可壓縮紊流中過度擴散率的脈動系數

ui——速度分量k——湍流脈動能

μ——粘性系數ρ——流體密度

μt——紊流粘性系數ε——湍流耗散率

C1ε、C2ε、C3ε——常系數

σk——系數k的紊流普朗特數

σε——系數ε的紊流普朗特數

Sk、Sε——用戶自定義的源項

固相采用Eulerian模型，計算式為[19-23]

(3)

式中ps——固體壓力ρs——固相密度

vs——固相速度vl——液相速度

vls——液固兩相速度傳遞系數

αs——固相體積分數

Ts——固相間的剪切力張量

Fs——固相外部體積力

Flift,s——固相升力Fvm,s——固相質量力

Kls——液相與固相間的動量交換系數

mls——液固兩相質量傳遞系數

固液兩相的連續性方程為

(4)

式中α1——液相體積分數

v1——液相速度ρ1——液相密度

ms1——固液兩相質量傳遞系數

1.2 物理模型

數值模擬計算的物理模型采用聲道布置為U形的DN25型超聲波熱量表測量管段，表長度為110 mm，測量段直徑為16 mm，反射柱前后長度為5 mm，換能器和反射柱直徑為10 mm，間距為70 mm，結構示意圖如圖1所示。

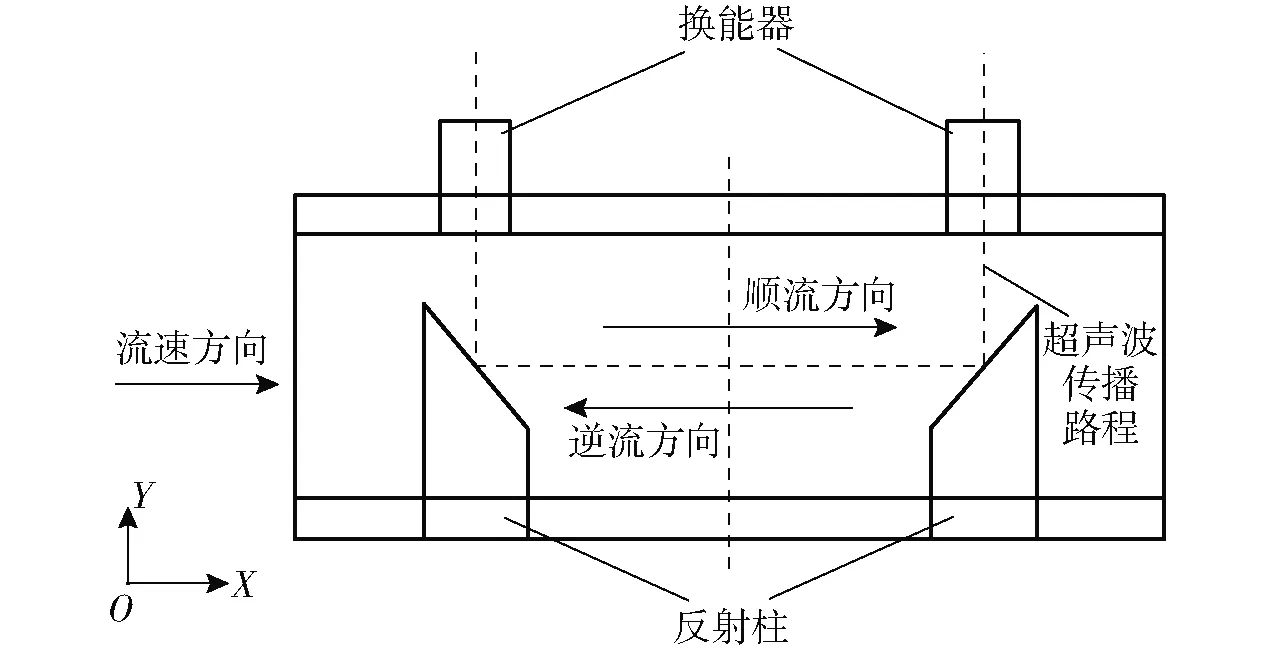
圖1 DN25型超聲波熱量表結構示意圖Fig.1 DN25 ultrasonic heat meter structure diagram

1.3 邊界條件

根據水質的實際情況，選取雜質體積分數為5%的流動進行研究，雜質采用CaCO3[10-11]，密度為2.7 g/cm3。入口邊界為Velocity Inlet，初始值按照充分發展狀態下流體速度分布設定，考慮到實際運行狀態和雷諾數變化，入口邊界條件取計量標準規定的5種流量[24]：0.07、0.14、0.35、1.05、3.50 m3/h。流動區域出口設定為自由出流條件，管壁為無滑移邊界。

1.4 網格劃分

反射柱前后長、測量段中間位置為圓柱體結構，直接采用結構網格。測量段結構不規則處采用非結構網格。為更好地探究雜質分布規律對聲波傳播影響，對測量段的網格進行加密。通過試算獲得網格數量滿足網格無關性的要求，模型的整體網格數需超過3.7×106個。

2 雜質顆粒分布規律及其對聲波傳播的影響

2.1 不同流量下雜質分布規律

流道中間位置的截面作為雜質體積分數取值面，重力沿圖1中Y軸負方向加載。如圖2所示，坐標原點在管道中心處。考慮到超聲波換能器的聲波輻射寬度為10 mm，雜質體積分數取值范圍為圖中陰影區域。將相同Y坐標處的雜質體積分數沿X軸方向做線平均，稱為該分布位置處的體積分數。

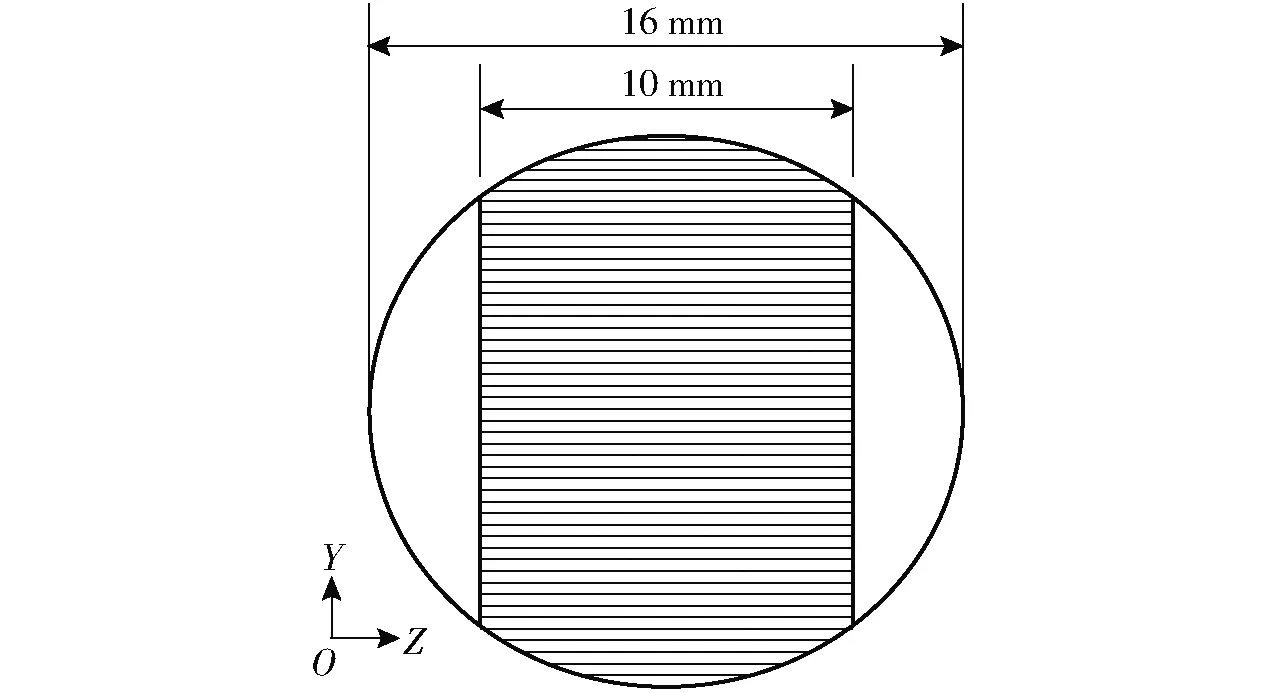
圖2 雜質分布計算截面示意圖Fig.2 Cross section diagram of impurity distribution observation

根據計算結果，取雜質顆粒直徑分別為0.01、0.02、0.05、0.10、0.20 mm工況下不同流量點沿Y軸雜質分布情況，如圖3所示。

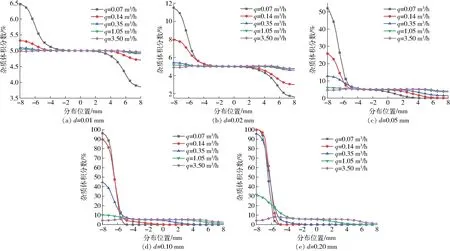
圖3 雜質在中心截面的分布規律Fig.3 Distribution rules of impurity in central section

圖3a為粒徑0.01 mm的雜質在中心截面隨流量變化的分布規律。從圖3a可以看出，流量大于0.35 m3/h的工況下，體積分數基本趨于5%，在-8 mm位置處最大，產生堆積。從0.14 m3/h的流量開始，整個雜質分布可以分為3個區域：底部沉積區，體積分數最大；中部均勻區，體積分數與平均值接近；頂部沉降區，體積分數最小。

當雜質粒徑增大為0.02 mm時，各流量點下的中心截面的體積分數分布曲線變化規律與粒徑為0.01 mm的基本一致，如圖3b所示。但底部最大體積分數增大，說明隨著粒徑的增大，沉積效果明顯。由上述兩種粒徑分布曲線中心區域(-5～5 mm)的雜質分布規律可知，該區域雜質體積分數基本保持一致。即對聲波傳播產生的反射、散射影響也是一定的，此種情況下可以通過流量系數進行修正，確保測量精度。

隨著雜質粒徑的繼續增大，當粒徑為0.05 mm時中心截面的雜質分布規律與之前相比產生明顯變化。如圖3c所示，在流量3.50、1.05 m3/h工況下，雜質體積分數基本保持一致；從流量0.35 m3/h開始，隨著流量的減小，底部雜質沉積逐漸增大，中間雜質保持一致的區域逐漸變小，頂部雜質體積分數逐漸變低，即在0.07～0.35 m3/h的流量區間內，雜質在中心截面的分布不穩定，對聲波的影響也不恒定，對測量產生影響。即在此粒徑流動下，流量1.05 m3/h以上工況，雜質在中心區域的分布一致，在流量0.35 m3/h工況下，雜質在中心區域的分布產生變化，隨著流量的減小，中心區域的雜質分布變小。

當雜質粒徑為0.10 mm時，雜質的分布規律與粒徑為0.05 mm的基本一致，如圖3d所示。在流量0.07 m3/h工況下，雜質基本沉積在-8～-5 mm的區域范圍內，隨著流量的增大，該區域開始變大。當流量達到1.05 m3/h，在中心區域體積分數基本一致。

當雜質粒徑繼續增大到0.20 mm時，雜質的沉積現象更加明顯，如圖3e所示。在流量0.07、0.14 m3/h時，雜質基本沉積在-8～-5 mm的區域，其他區域的雜質含量基本為零，即在這兩種流量下，雜質不會對聲波傳播產生影響；在流量0.35 m3/h下，雜質的沉積范圍增大到-2 mm，該范圍已經達到聲波傳播的中心區域，開始對聲波的傳播產生影響，隨著流量的繼續增大，中心范圍的雜質分布變大，當流量達到3.50 m3/h時，中心區域的雜質分布基本區域一致。

2.2 雜質分布對聲波傳播及測量的影響

通過雜質分布規律(圖3)分析可知，在中心截面雜質的分布規律與顆粒粒徑、流量有關。雜質粒徑越小，流量越大，雜質分布越均勻；雜質粒徑越大，流量越小，雜質分布越復雜。超聲波信號傳播路徑上的雜質會影響測量精度，為研究該路徑雜質的分布情況，分別對0.07、0.35、3.50 m3/h 這3種流量工況下兩相流流場進行模擬，這3個流量點分別對應層流流動、雷諾數較小的湍流流動、雷諾數較大的湍流流動，流道截面內不同粒徑雜質分布云圖如圖4～6所示。

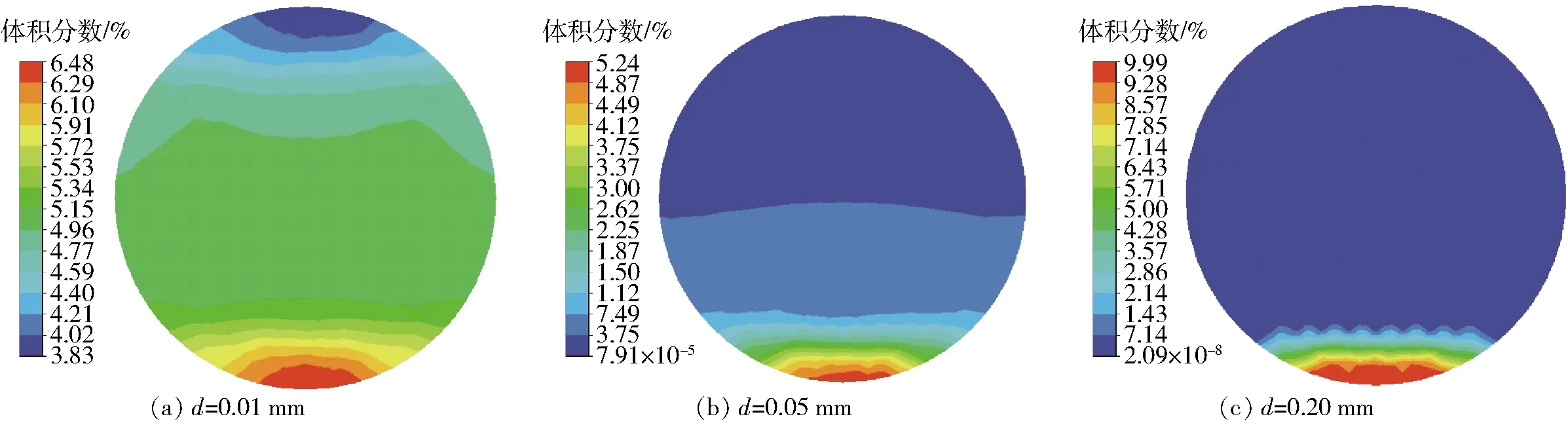
圖4 流量0.07 m3/h工況下雜質分布云圖Fig.4 Concentration distribution diagrams of impurities under flow condition of 0.07 m3/h

如圖4所示，在小流量工況下，隨著雜質粒徑的增大，雜質分布產生變化。當d=0.01 mm時，雜質區域均勻分布，中心區域體積分數一致，對聲波傳播和測量精度影響規律一致；當d=0.05 mm時，雜質分布不均勻，從上至下體積分數逐漸增大，中間區域處于不穩定狀態，對聲波傳播及測量影響最大；當d=0.20 mm時，雜質基本沉積在底部區域，中間區域的雜質分布幾乎為零，對聲波傳播及測量精度無影響。

如圖5所示，流量0.35 m3/h工況下，當d=0.01 mm時，雜質區域均勻分布，中心區域的體積分數一致，對聲波傳播和測量精度影響規律一致；當d=0.05 mm時，雜質分布在上部分區域逐漸變大，變化區域范圍進入了中心區域，對聲波傳播和測量精度產生影響；當d=0.20 mm時，雜質大部分沉積在底部，相比小流量工況，底部區域增大，結合圖4的規律，有一部分雜質進入到中心區域，對聲波傳播和測量精度產生影響。

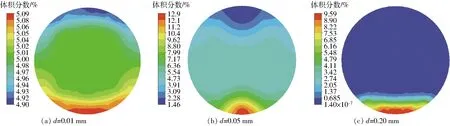
圖5 流量0.35 m3/h工況下雜質分布云圖Fig.5 Concentration distribution diagrams of impurities under flow condition of 0.35 m3/h

如圖6所示，當流量為3.50 m3/h時，隨著雜質粒徑的增大，分布由原來的均勻分布逐漸向底部沉積，當d為0.01、0.05 mm時，處于均勻分布，對聲波傳播及測量的影響規律一致；當d=0.20 mm時，雜質較多沉積在底部，并且影響中心區域，對聲波傳播和測量精度產生影響。

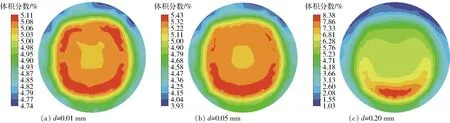
圖6 流量3.50 m3/h工況下雜質分布云圖Fig.6 Concentration distribution diagrams of impurities under flow condition of 3.50 m3/h

3 實驗及分析

根據上述數值分析可知，信號傳播路徑上雜質粒徑和濃度越大，對聲波的傳播影響也越大，勢必對超聲波的測量精度產生影響，因此本文通過實驗研究獲得雜質對超聲波熱量表檢測精度的影響。分別在清水、加體積分數為5%的不同粒徑的CaCO3顆粒兩相流中進行流量測量，與標準流量計數值對比，進行誤差分析。被測表為DN25 型超聲波熱量表，精度等級為2級。

測試實驗臺如圖7所示。該流量檢測實驗臺的誤差精度為0.1%，符合熱量表檢測裝置要求[25]。本文實驗選用稱量法進行檢測。

圖7 流量檢測實驗臺Fig.7 Flow test bench

根據計量檢測規程和數值模擬計算結果，實驗研究測量流量分別為0.07、0.14、0.35、1.05、3.50 m3/h。

經過篩選，CaCO3顆粒密度為2.7 g/cm3，粒徑為0.20、0.10、0.05、0.02、0.01 mm，體積分數為5%。在流量檢測實驗臺的水箱中均勻混合，再對超聲波熱量的檢測精度進行測試。

超聲波熱量表誤差計算公式為

(5)

式中q1——被檢測表的流量值

q——實驗臺測得的標準流量值

采用的實驗方案為稱量法，通過標準秤測量流過熱量表的流體質量，進而計算流量q。

不同流量點超聲波熱量表流量測量值的相對誤差隨CaCO3粒徑變化曲線如圖8所示。

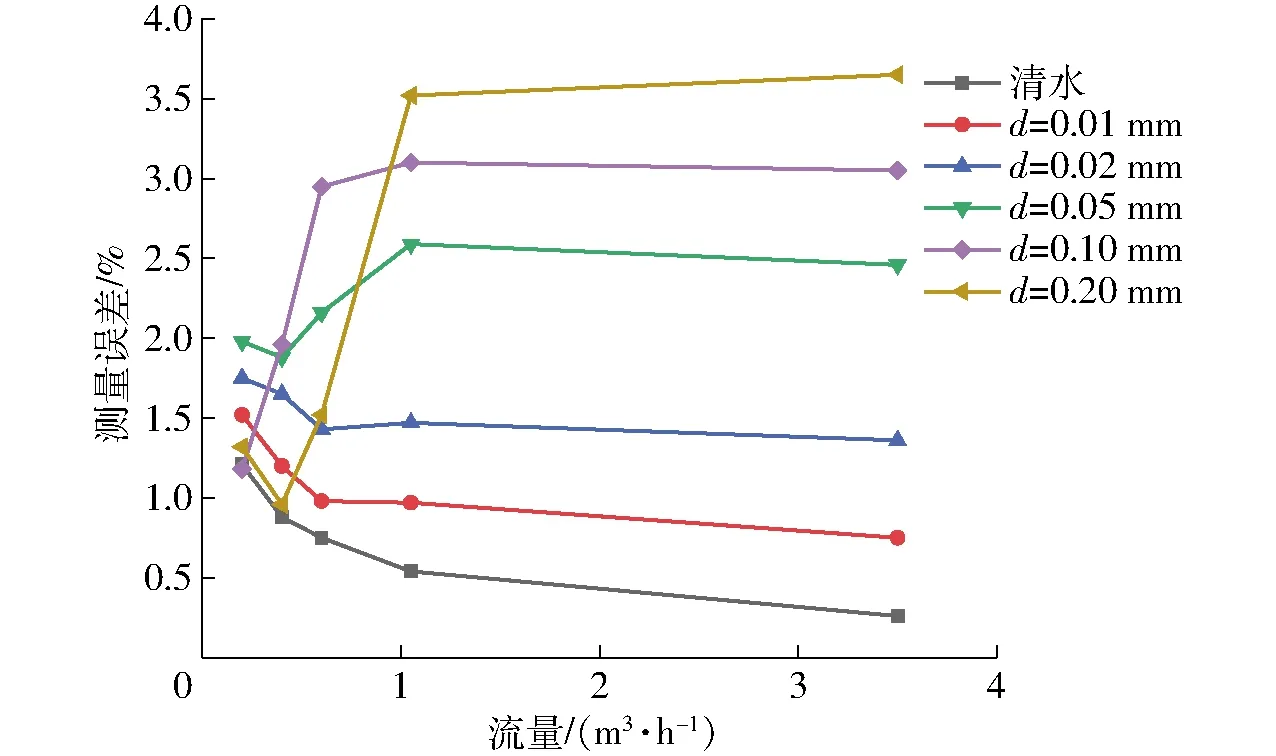
圖8 誤差隨碳酸鈣粒徑變化曲線Fig.8 Error curves with calcium carbonate concentration change

如圖8所示，清水工況下，超聲波熱量表在不同流量下的測量誤差變化小于1%；隨著粒徑的增大，測量誤差變大。當顆粒物分布相同時，粒徑越大對聲波的反射能力越強，聲波衰減越大，如圖9所示。

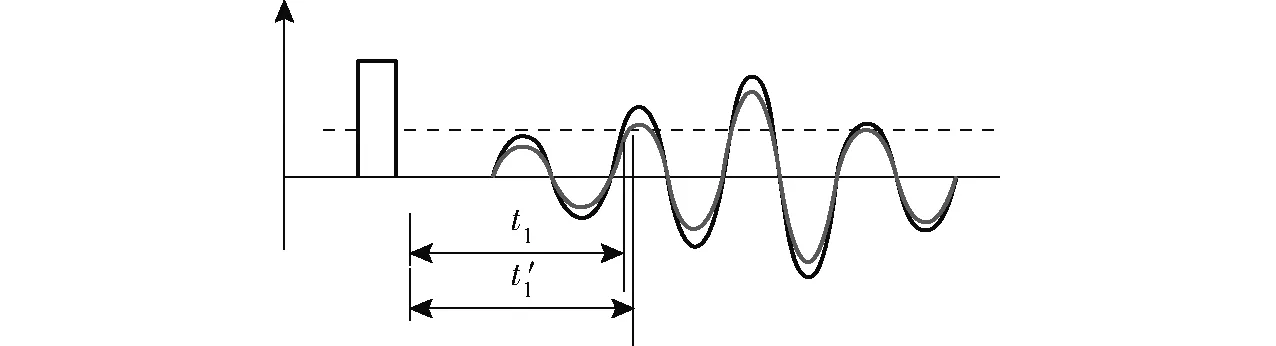
圖9 接收波形放大示意圖Fig.9 Waveform enlarged schematic

由于雜質存在使聲波產生衰減，時間由原來的t1變為t′1，導致時差變大，產生正向誤差，所以聲波衰減越大，產生的誤差越大。

雜質粒徑為0.01、0.02 mm的情況下，測量誤差相比純水有所增大，所有流量規律基本一致。當粒徑為0.05 mm時，所有流量下的誤差增大，特別是當流量從0.35 m3/h開始，增大幅度變大，由圖3c可知，隨著流量的增大，中心區域的雜質體積分數變大，所以誤差增大。當粒徑為0.10 mm，流量為0.07 m3/h時，誤差幾乎與純水一致，此后隨著流量的增大，誤差開始增大，且增大幅度逐漸變大。由圖3d可以看出，流量為0.07 m3/h時，雜質基本沉積在底部，中心區域雜質體積分數基本等于零，所以對測量誤差無影響，隨著流量的增大，雜質在中心區域的體積分數也逐漸增大，誤差變大。當粒徑為0.2 mm時，流量為0.07、0.14 m3/h時，測量誤差與純水基本一致，之后隨著流量的增大誤差增大，對比圖3e，流量為0.07、0.14 m3/h時，雜質分布沒有進入中心區域，因此誤差不變，0.35 m3/h雜質進入中心區域，誤差開始增大，直至3.50 m3/h時，雜質分布在全部中心區域，誤差最大。

流量0.35 m3/h為曲線變化分界點，在此流量點之后，不同粒徑的測量誤差開始逐漸趨于水平。該誤差規律與上述數值模擬計算分析一致，驗證了本文數值計算的正確性。

4 結論

(1)通過對雜質分布規律的分析獲得中心區域分布一致的工況，即雜質粒徑在0.02 mm以下，或者流量在1.05 m3/h以上時，該工況下中心區域的雜質濃度分布基本保持一致，對聲波的傳播和測量精度影響規律一致。

(2)通過分析獲得雜質在中心區域分布幾乎為零的工況，即當雜質粒徑為0.1 mm、流量為0.07 m3/h，或者雜質粒徑為0.2 mm、流量小于0.14 m3/h，該工況下聲波傳播不受雜質的影響，對測量精度無影響。

(3)通過分析獲得雜質分布不穩定工況，即雜質粒徑在0.05 mm以上時，隨著雜質粒徑的增大，雜質逐漸向底部靠攏，且隨著流量的降低，中心區域的雜質分布減小。該工況下聲波的傳播受雜質顆粒粒徑和流量的綜合影響，對測量精度影響最大。