鐵路風速傳感器現場校準裝置研究

湯勇，林建輝，鐘文生，杜高峰

(西南交通大學 牽引動力國家重點實驗室，四川 成都 610031)

0 引言

隨著國內列車速度的不斷提高，風速的監測對列車運行的安全性越來越重要。通過風速傳感器可以對風速進行全天候的監測，從而為列車的正常運行提供保障。但風速傳感器因長期在室外使用，受到惡劣天氣的影響，其測量的精度會有一定的下降。目前國內風速傳感器的現場校準都是針對風杯式的，利用機械傳遞方法強制風速傳感器風杯軸轉動，從而完成校準。但這種方法對WXT520超聲波風速傳感器并不適用,因此研究出一種針對超聲波風速傳感器現場校準的方法具有非常重要的現實意義。

1 WXT520風速傳感器工作原理

WXT520是目前鐵路上廣泛使用的風速傳感器，其工作原理是利用超聲波時差法即超聲波在順風和逆風時的傳播速度不同來實現對風速的測量。其結構主要由3個等間距的超聲波收發探頭組成，3個探頭位于同一水平面上，組成一個變換器陣列,如圖1所示。通過測量超聲波沿變換器陣列所形成的3條路徑的傳送時間(雙向)，即測量6個傳送時間，就可以算出3條超聲波路徑中每條路徑的風速。通過信號處理技術，選用質量最好的兩條陣列路徑來計算風速大小。超聲波風速傳感器的現場校準需要持續穩定均勻的風速，本文設計的低速風洞可以滿足校準要求。

圖1 WXT520風速傳感器結構圖

2 風洞結構設計

2.1 總體結構

目前風洞的基本形式有兩種：開路式風洞和回路式風洞[1]。本次設計風洞的型式為圓形開路式風洞，主要結構包括穩定段、收縮段、試驗段和擴散段等。根據風洞設計理論確定各段的尺寸，本次設計風洞的總體尺寸為：2.05m×0.6m×0.6m(長×寬×高)，風洞結構如圖2所示。

1—蜂窩器；2—阻尼網。圖2 風洞結構圖

2.2 工作原理

風機產生的風源到達穩定段后，經過一段距離，通過蜂窩器和阻尼網。蜂窩器可以將氣流導直，使其平行于風洞軸線，同時將氣流中的大尺度旋渦分割成小旋渦，從而加快旋渦衰減，然后再通過3層阻尼網使氣流分布更趨均勻和穩定；收縮段對經過穩定段的氣流進行加速，氣流速度按面積比而增加，而脈動速度保持不變，紊流度進一步得到改善，使得收縮段出口氣流保持均勻、平直且穩定，小旋渦得到進一步衰減，使氣流速度分布更趨均勻和穩定[2]并得到均勻且穩定的試驗段氣流對風速傳感器進行校準；通過擴散段將氣流擴散出去。

2.3 試驗段設計

試驗段是整個低速風洞設計的關鍵，直接影響傳感器校準的結果。一般試驗段的截面形狀有圓形、方形、三角形、橢圓形以及長方形。在相同的條件下，通過橢圓形界面的氣流最均勻，圓形次之，長方形再次之。但是由于橢圓形截面加工工藝復雜且不易安裝，故本次設計選取圓形截面作為試驗段的截面形狀。WXT520風速傳感器的實際尺寸為：0.115m×0.115m×0.238m(長×寬×高)。根據傳感器的實際尺寸，選取試驗段的直徑D=0.4m。由相關資料可知[1]，試驗段長度公式為：

L=2.0D～2.5D

(1)

由于本次設計的是微型可移動風洞，故風洞的尺寸應盡量小。選取試驗段的長度L=0.8m，最后得到的試驗段是長度為0.8m、直徑為0.4m的等截面圓形管道。

2.4 收縮段設計

收縮段主要是使來自穩定段的氣流均勻加速，達到試驗段需要的流速，并改善試驗段的流場品質。收縮段的設計應滿足以下要求[1，3-4]：1) 氣流單調增加，避免氣流在洞壁發生分離；2) 出口處氣流分布均勻，方向平直且穩定；3) 收縮段的長度要適中，既要符合結構要求又要使收縮壁的過渡不至過分劇烈而造成流動的分離和擾動。

收縮段的性能主要取決于兩個因素：一是收縮比，即收縮段的進口截面積與出口截面積之比；二是收縮曲線[5]。風洞收縮比的大小，主要取決于以下因素：對試驗段氣流的均勻性和紊流度的要求，風洞的能量比以及風洞造價。本次設計主要考慮的是風洞的尺寸及造價，故選取小的收縮比，取收縮比為2。收縮段的長度一般可采用進口直徑的0.5～1.0倍[1]，本次設計取收縮段的入口直徑為0.55m，長度為0.4m。收縮段曲線的設計采用的是Batchelor-Shaw提出的理想不可壓流的一維流公式(認為每個截面上的氣流參數是均勻的)，收縮段曲線方程為：

(2)

其中：F1、F2和F分別為收縮段進口、出口及任意x處的截面面積；L為收縮段的長度。

2.5 穩定段設計

穩定段通常為等截面管道，下游與收縮段相接，所以其面積大小取決于風洞收縮比的要求[1，6-7]。穩定段設計首先要保證蜂窩器和多層阻尼網的安裝。穩定段尺寸與收縮段入口尺寸一致，一定長度的等截面管道有利于導直氣流、穩定氣流和均勻流場，小收縮比風洞穩定長度應該為直徑的1.0～1.5倍[1,6-7]。本次設計穩定段長度為直徑的1倍，即0.55m。

蜂窩器網格有圓形、方形、六角形和梯形等，其中六角形網格最為理想，該網格的損失系數小，氣流壓力損失小，對降低湍流度有顯著效果[1]。影響蜂窩器性能的主要參數是蜂窩長度L和孔徑M。本文設計的蜂窩孔徑為2mm，根據經驗公式[1]:L/M=5～10，蜂窩器的長度取值為15mm。

阻尼網位于蜂窩器和收縮段之間，阻尼網可降低蜂窩器后的氣流旋渦，以減少穩定段氣流的湍流強度，使穩定段流場更均勻。阻尼網的選擇與遲滯系數β有關，由相關資料可知[1]，遲滯系數β的計算公式為：

(3)

其中d和l分別為網絲直徑和網孔邊長。

如果網絲的遲滯系數太小，網后氣流可能會出現不穩定；如果遲滯系數太大，整流作用將會削弱，一般低湍流度風洞多采用0.57<β<0.6的大遲滯系數[8]。對于同一遲滯系數的阻尼網，網絲直徑越小，阻尼網效果越好，且多層網組比單層網的效果好[9]。本次在穩定段設計3層阻尼網，網絲直徑為0.4mm，網孔邊長為2mm。

2.6 風機選型

對于低速風洞，由于馬赫數很小，氣流可看作不可壓縮流體。根據風速傳感器檢定所需的最大風速和試驗段的直徑，由流量計算公式：

Qmax=S·Vmax

(4)

其中:S為試驗段的截面面積;Vmax為檢定的最大風速;Qmax為試驗段所需的最大風量。

由公式(4)可得試驗段所需的最大風量值為3.77m3/s(約為13572m3/h)。由于風速經過收縮段到達試驗段時，風速約為入口風速的2倍，故本次設計中選擇的風T35-11型、機號為5的軸流風機，該風機的標稱風量為9133m3/h，功率為0.75kW，葉輪直徑為500mm。采用tesech變頻器對風機轉速進行控制，該變頻器采用脈動輸入頻率控制和先進的三相切換兩相控制技術，具有運算速度快、自動程序運轉控制、自動調整加減速、自動轉矩補償、自動滑差補償、超低噪聲及高過載能力等諸多優點[2]。

2.7 擴散段設計

擴散段主要是使氣流通過試驗段后能夠降速增壓，以減少整個風洞的能量損失和對外界環境的影響。通常對于不可壓縮流體來說，面積比不超過2.5，擴散角控制在8°～10°以內為宜。本次設計選取面積比為2.5，擴散角為9°，故計算得到擴散段最大孔徑為0.6m，長度為0.3m。

3 皮托管選型

皮托管又名“空速管”，是法國人Henri-Pitot發明創造的。皮托管的測量原理依據是理想不可壓縮氣體下的伯努利方程，即在均勻穩定的理想流場內，同一流線上任意兩點的動能、重力勢能及壓力勢能之和是一個常量[10]。其具體公式為：

(5)

式中:ρ為流體的密度;v為流體的速度;g為重力加速度;P為流體的壓力勢能，cost是流體在該點的總能量，為一常數。

皮托管一般有兩種常見結構：L型皮托管和S型皮托管。L型皮托管在有灰塵情況下容易造成堵塞，影響測量精度，故本次設計選用S型皮托管，其結構如圖3所示。

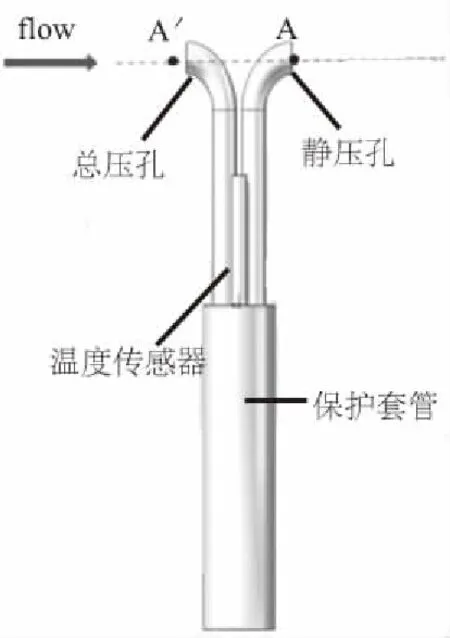
圖3 S型皮托管

4 仿真分析

首先利用CATIA根據傳感器實際尺寸建立傳感器的三維模型，如圖4所示。然后再把整個裝置導入ICEM中進行網格劃分。網格劃分時，因蜂窩器和阻尼網為薄片式結構，主要起整流作用，對氣體流動產生的阻礙較小，因此忽略,網格劃分如圖5所示。最后把劃分好網格的模型導入Fluent進行流體計算和仿真分析。設定邊界條件入口風速和出口壓力，其中出風口與外界相連，故出口壓力為0，分別對入口風速為2m/s、5m/s、10m/s、15m/s、20m/s、30m/s時風洞內部流場的均勻性和穩定性進行仿真分析，得出試驗段軸向風速分布圖和傳感器橫截面壓力梯度分布圖，如圖6和圖7所示。

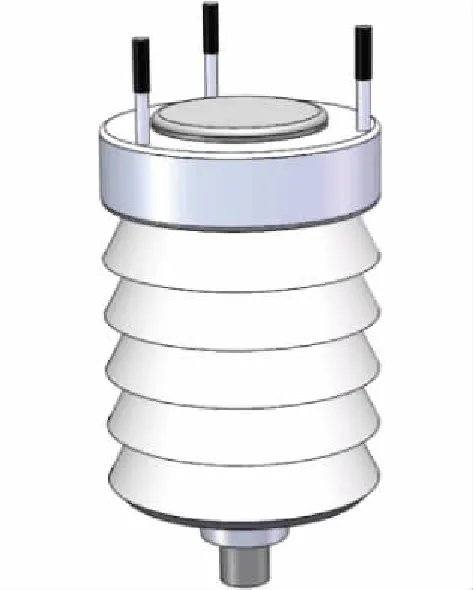
圖4 傳感器三維模型

圖5 風洞裝置網格劃分

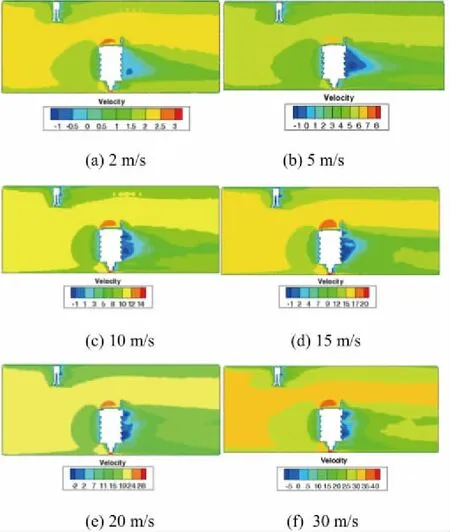
圖6 實驗段軸向風速分布圖

圖7 傳感器橫截面壓力分布圖

從圖6和圖7可知，雖然皮托管和傳感器使風洞內部流場發生了變化，但是皮托管和傳感器所在區域附近的流場仍然趨于均勻穩定，且皮托管和傳感器探頭接收到的風速也仍然是一樣的。模擬仿真結果表明該小型風洞能夠達到風速傳感器現場檢定要求。

5 試驗驗證分析

為了驗證模擬仿真結果的可靠性，在實驗室里進行了該試驗。試驗在5種不同風速下進行，并測出了3組數據,把皮托管測量出的風速值作為當前的標準風速值，把傳感器測量的風速值與標準值進行對比分析。試驗裝置和數據如圖8和表1所示，第1組試驗速度分析如圖9所示。

表1 不同風速下的測量數據 單位：m/s

圖8 風洞試驗裝置臺

圖9 第1組試驗速度分析

由風洞設計原理可知，風洞內部流場越穩定，風洞內各點的風速值越接近。從表1和圖9中可以看出，隨著設定風速值的逐漸增大，皮托管和傳感器所測得的風速值越接近，誤差越小,即風洞內部流場隨著設定風速值的增大而趨于穩定。3組試驗數據中最大誤差出現在第3組，誤差值為0.22m/s，而傳感器允許的最大誤差為±0.3m/s，故該微型低速風洞完全滿足傳感器校準精度要求。在現場進行傳感器的校準時，可選用較大的風速值，這樣可以提高校準精度。

6 結語

本文根據鐵路上廣泛使用的風速傳感器，設計了一種可移動微型低速風洞裝置。該裝置不僅可以用于風速傳感器的室外校準，也可用于教學實驗。與之前的校準方法相比較，該裝置大大縮短了傳感器的校準周期，降低了校準成本，并且風洞洞體具有結構簡單、質量輕、易加工、成本低等特點。在進行現場檢定時，可把風洞設備固定在鐵路上專用的維修車上，從而在現場完成風速傳感器的檢定。由此可見，本文所設計的裝置具有重要的工程意義。