平面向量

一、填空題

1.已知a，b為任意平面向量，現有下列四個結論：①|a+b|=|-a-b|；②|a-b|=|b-a|；③|a-b|=|a|-|b|；④|-ab|=-|a|-|b|.其中正確的為_________.（寫出序號）

2.已知平面向量a，b滿足|a|=4，|a+b|=5，|a-b|=6，則|b|=________.

3.（2019年嘉興調研）已知點A（2，3），B（4，5），C（7，10），若R），且點P在直線x-2y=0上，則λ的值為________.

4.（2019年全國卷Ⅰ）已知非零向量a，b滿足|a|=2|b|，（a-b）⊥b，則a與b的夾角為________.

5.設正△ABC的邊長為4，則=________.

6.若平面向量a，b滿足|a|=1，|b|≤1，且以向量a，b為鄰邊的平行四邊形的面積為，則a與b的夾角θ的取值范圍是________.

7.在△ABC中，M是BC的中點，AM=3，BC=10，則=________.

8.在平行四邊形ABCD中，已知AB=2，AD=1，∠DAB=60°，點M為AB的中點，點P在BC與CD上運動（包括端點），則的取值范圍是________.

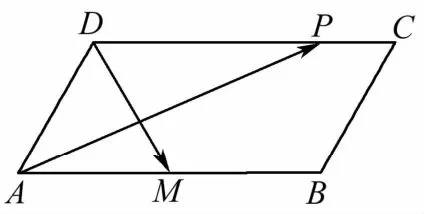
（第8題）

9.（2019年如皋調研）已知O是面積為4 的△ABC內部一點，且有，則△AOC的面積為________.

10.若△ABC的一邊AB的長為6，，則△ABC面積的最大值等于________.

二、解答題

11.在平面直角坐標系xOy中，點A（2，5），B（3，1），C（6，3）.

（1）求以線段BA，BC為鄰邊的平行四邊形兩條對角線的長；

（1）求m=f（θ）的關系式；

13.已知扇形AOB的半徑等于1，∠AOB=120°，P是圓弧上的一點.

（1）若∠AOP=30°，求的值；

14.（2020年蘇州市調研）已知向量m=.

（1）若m·n=1，求的值；

（2）記f（x）=m·n，在△ABC中，角A，B，C的對邊分別是a，b，c，且滿足（2a-c）·cosB=bcosC，求函數f（A）的取值范圍.