鍛造液壓機雙缸同步控制系統研究

李勝永

(南通航運職業技術學院，江蘇 南通 226010)

引言

工業發展對鍛造液壓機的控制精度需求越來越高[1]。現在鍛造液壓機多采用雙液壓缸作為驅動機構，容易出現2個液壓缸不同步，導致偏載和機械結構卡死，因此需采用合理的同步控制策略提高兩缸同步精度。

為提高雙缸同步控制精度，各科研機構做了相關研究[2]。李栓柱等[3]為了提高雙缸鍛造液壓機的同步控制精度，設計了免疫神經網絡PID控制器，該控制器具有同步跟蹤誤差小、魯棒性高等優勢。裴紅蕾等[4]設計了由內環壓力控制和外環位置控制級聯的二級控制器以提高重型鍛造液壓機同步控制精度，該控制器具有很高的位置控制精度且魯棒性很好。管國棟等[5]針對80 MN鍛造液壓機采用了西門子PLC與Trio控制器相結合的方案，該方案獲得了預期控制效果。董春芳等[6]設計了一種交叉耦合同步控制方式，通過通道狀態比較，其雙缸同步控制精度較高。HEARNS G等[7]采用定量反饋理論(QFT)，并將此應用到雙液壓缸驅動軋機設備中，控制效果較好。SUN等[8]提出了一種非線性同步控制算法用于雙缸同步控制。MASTELLONE S等[9]基于李雅普諾夫穩定性理論，采用主從控制方法，實現機器人的協同工作。王燕等[10]采用電液伺服閥，設計了電液同步多通道加載系統。上海市隧道工程采用液壓同步頂進技術，利用PID控制器實現對液壓泵驅動電機的控制，通過調節液壓泵輸出流量，實現位移和壓力同步控制[11]。BYUN等[12]提出了一種由2個擾動觀測器和1個同步控制器組成的系統，該控制系統降低了扭曲干擾對同步偏差的影響。LI K等[13]采用偽導數反饋方法實現了雙液壓缸電梯的同步提升，在 400 mm行程中，同步偏差保持在± 2 mm。

對雙缸同步控制的研究可以看出，目前針對雙液壓缸同步控制系統的研究較多，但針對鍛造液壓機的雙缸同步控制系統的研究較少。針對這種情況，本研究設計了鍛造液壓機雙缸同步控制系統，并對系統中雙缸同步控制這一關鍵技術進行研究。采用誤差反饋的同步控制結構實現雙液壓缸同步精確控制，利用遺傳算法進行了PID參數整定，為提高鍛造液壓機雙缸同步控制精度提供理論依據。

1 鍛造液壓機雙缸同步控制系統設計

為實現鍛造液壓機兩液壓缸高精度同步調整，雙缸同步控制系統原理如圖1所示設計。兩液壓缸活塞桿與活動橫梁連接，活動橫梁垂直運動，實現鍛壓鍛件。

系統具體控制過程可簡述為：系統啟動后，位移傳感器1和2檢測此時液壓缸1和2的活塞桿位移，并將位移信號反饋給控制器，控制器控制比例閥1和2動作，對液壓缸1和2進行油液補充和減小，從而調整液壓缸1和2的活塞桿位移，實現其同步控制。

從控制過程可知，系統同步控制精度主要取決于控制器中同步控制策略，此決定著鍛造液壓機雙缸同步控制性能。

2 同步控制系統數學模型建立

由上述系統工作過程可知，為實現高精度的雙缸同步控制，關鍵在于對系統中的液壓缸位置進行精確控制。

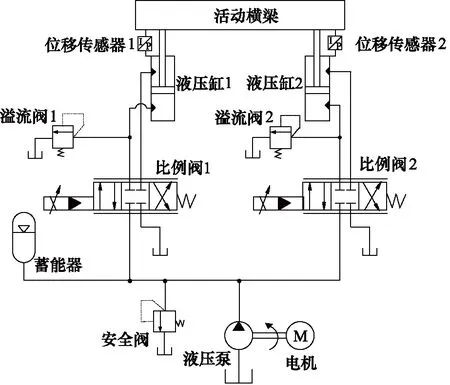
圖1 鍛造液壓機雙缸同步控制系統

液壓缸位置控制系統原理如圖2所示。此系統中主要包括比例放大器、比例方向閥、閥控液壓缸系統以及位移傳感器[14-16]。

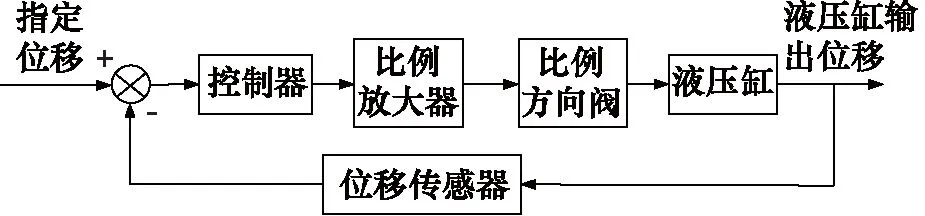
圖2 液壓缸位置控制系統原理圖

液壓缸位置控制系統數學建模過程目前采用的方法較為成熟，具體建模過程此處不詳細介紹，下面將各環節的數學模型列出。比例放大器數學模型為：

i=KaΔu

(1)

式中，Δu—— 比例放大器輸入電壓，V

i—— 比例放大器輸出電流，A

Ka—— 比例放大器放大系數，A/V

比例方向閥傳遞函數為[17]：

(2)

式中，Xv—— 比例方向閥閥芯位移，m

Kb—— 比例閥閥芯位移與電流增益系數，m/A

wm—— 比例方向閥固有頻率，rad/s

ξm—— 比例方向閥阻尼比

采用了非對稱液壓缸，非對稱液壓缸有桿腔和無桿腔有效作用面積不相等，因此液壓缸活塞桿伸出和縮回的數學模型不相同[18]。活塞桿伸出時活塞桿位移Xp對比例閥閥芯位移Xv的傳遞函數為：

(3)

式中,Kq1—— 比例閥流量增益，m2/s

A1—— 無桿腔有效作用面積，m2

wh1—— 活塞桿縮回時液壓固有頻率，rad/s

ξh1—— 液壓阻尼比

活塞桿縮回時活塞桿位移Xp對比例閥閥芯位移Xv的傳遞函數為：

(4)

式中，Kq2—— 比例閥流量增益，m2/s

A2—— 有桿腔有效作用面積，m2

wh2—— 活塞桿縮回時液壓固有頻率，rad/s

ξh2—— 液壓阻尼比

位移傳感器數學模型為：

uf=KfXp

(5)

式中，Kf—— 位置反饋增益，V/m

uf—— 位移傳感器反饋電壓，V

Xp—— 液壓缸輸出位移，m

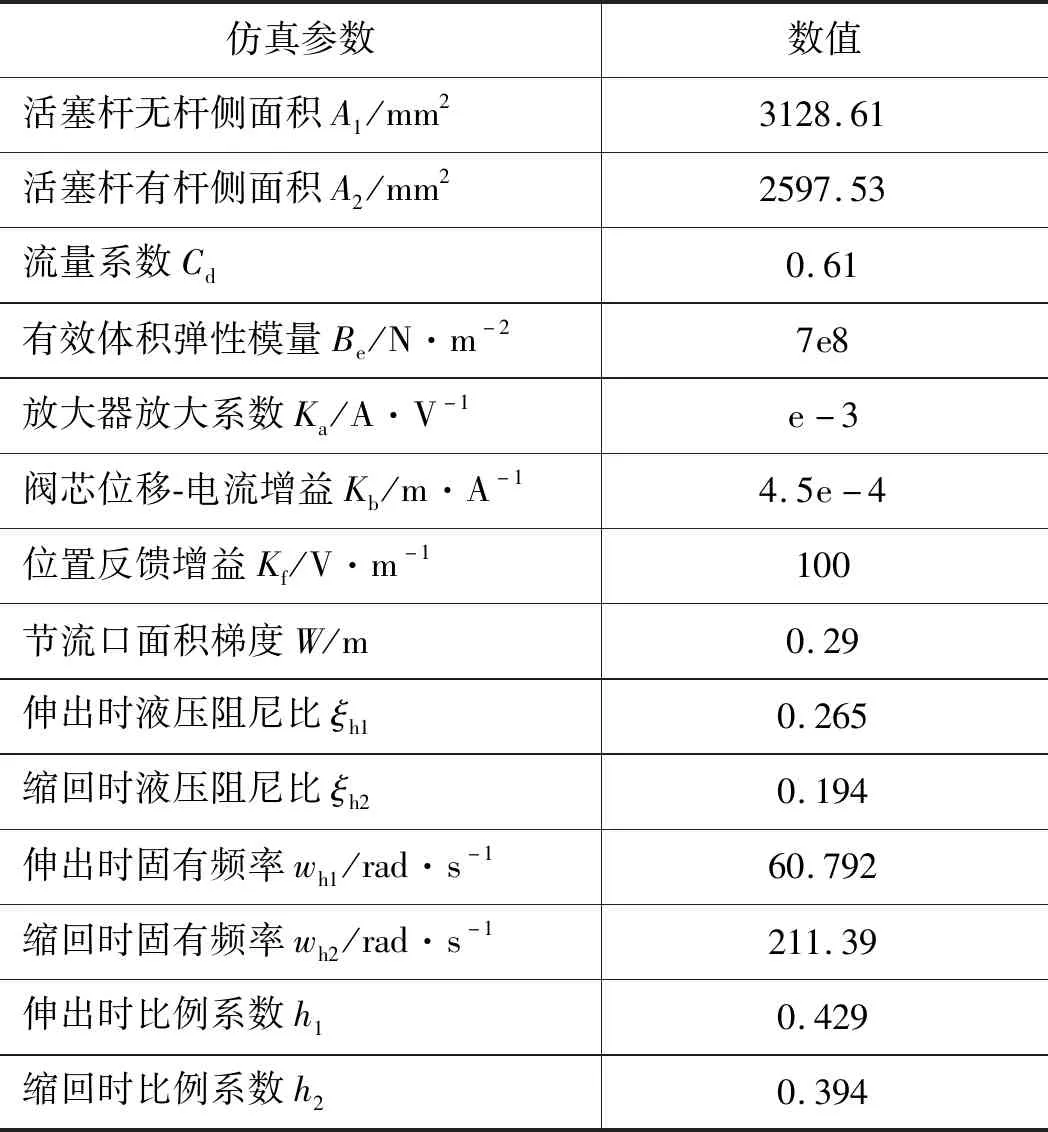
表1 技術參數

系統主要技術參數如表1所示，將參數代入式(3)、式(4)，得到活塞桿伸出狀態下活塞位移Xp對比例閥閥芯位移Xv的傳遞函數為：

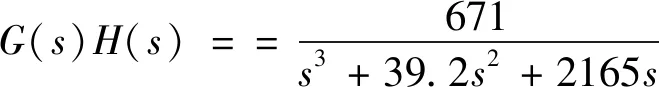
(6)

活塞桿縮回狀態下活塞位移Xp對比例閥閥芯位移Xv的傳遞函數為：

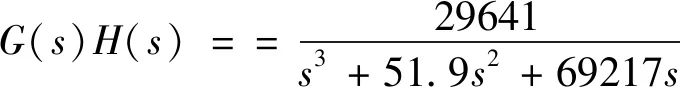
(7)

3 雙缸同步控制系統控制策略研究

目前，“串聯型”和“并聯型”同步控制結構在同步系統中較為常用[19]。“串聯型”控制結構如圖3所示。“并聯型”控制結構如圖4所示。

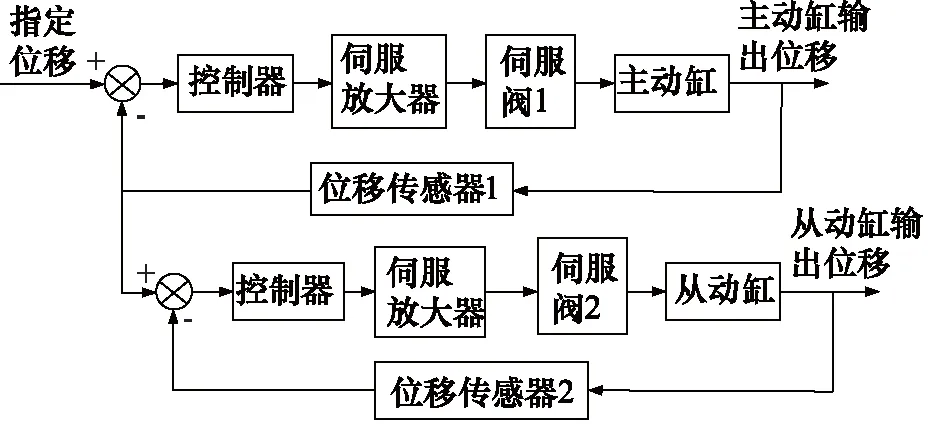
圖3 “串聯型”同步控制結構

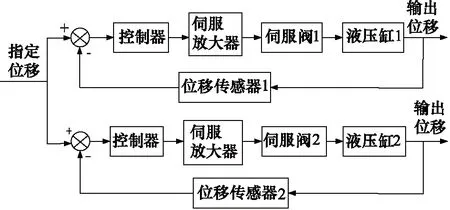
圖4 “并聯型”同步控制結構

為驗證“串聯型”和“并聯型”同步控制結構控制效果，在MATLAB/Simulink中建立仿真模型，并且控制器采用PID控制器。

首先采用遺傳算法實現對PID參數的整定。系統采用種群規模為n=50，交叉概率為pc=0.9，變異概率為pm=0.2，最大迭代次數N=500進行遺傳迭代尋優。采用時間誤差絕對值積分性能指標(ITAE)作為參數尋優的適應度函數，如式(8):

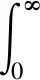
(8)

經過500代進化，可獲得液壓缸活塞桿2種狀態下參數整定結果，如表2和表3所示。

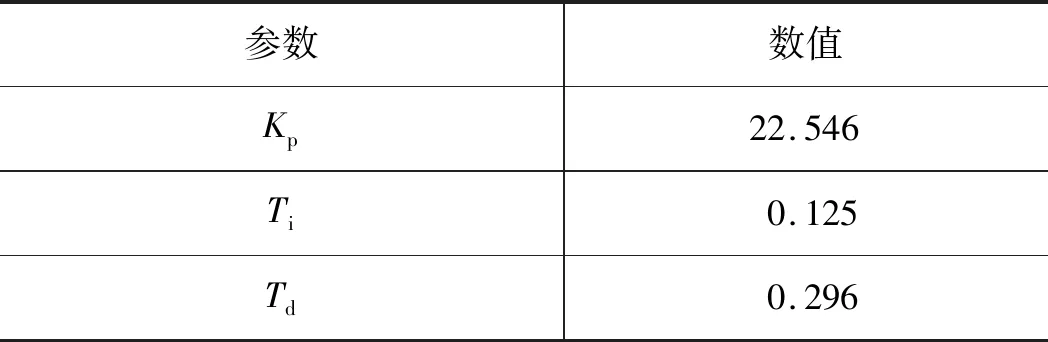
表2 活塞桿伸出時參數整定結果

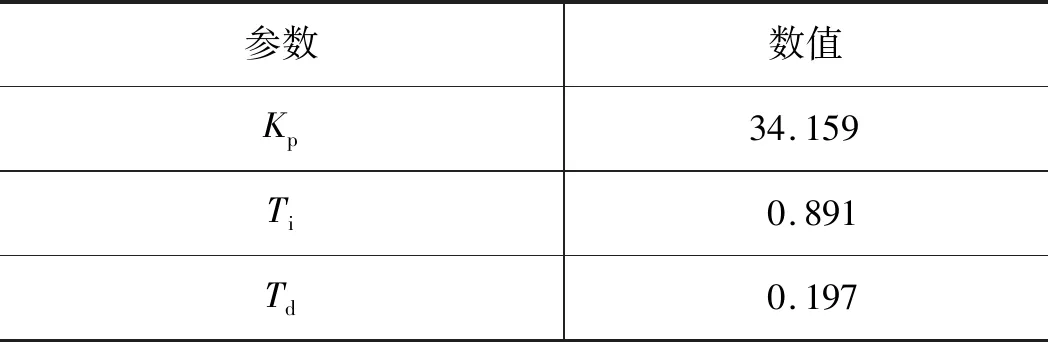
表3 活塞桿縮回時參數整定結果

對系統施加階躍信號，活塞桿伸出狀態下運行仿真結果如圖5～圖8所示。不同控制結構下仿真結果對比如表4所示。

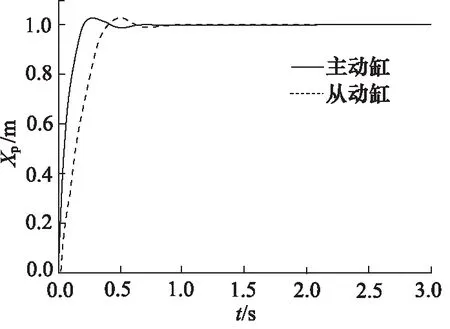
圖5 “串聯型”控制階躍響應曲線(活塞桿伸出)

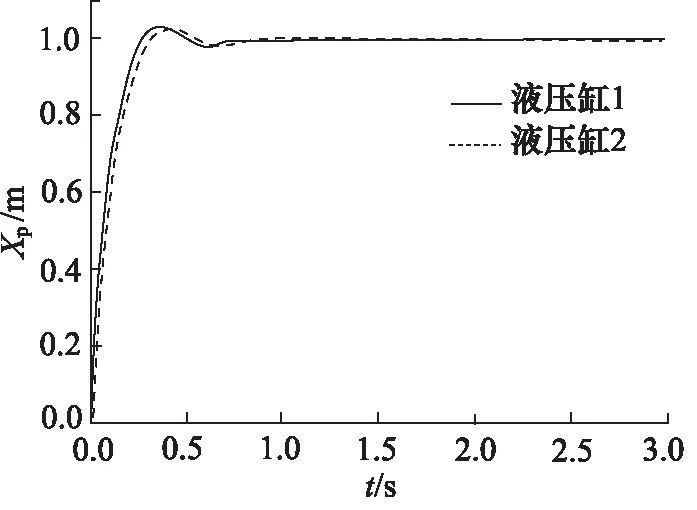
圖6 “并聯型”控制階躍響應曲線(活塞桿伸出)

由表4可得，在活塞桿伸出狀態下，“并聯型”相比“串聯型”最大同步誤差減小了80.35%；達到穩態同步誤差的調整時間增加了28.42%；串聯型存在0.001 m的穩態同步誤差，而并聯型穩態同步誤差為0。

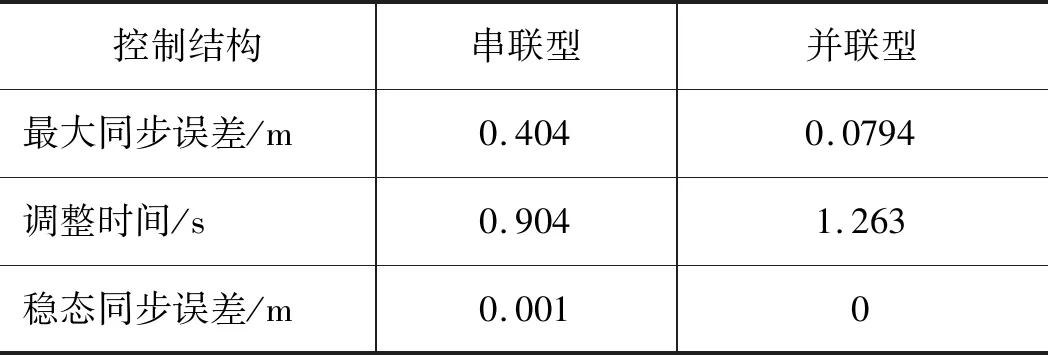
表4 兩種結構下仿真結果對比(活塞桿伸出)

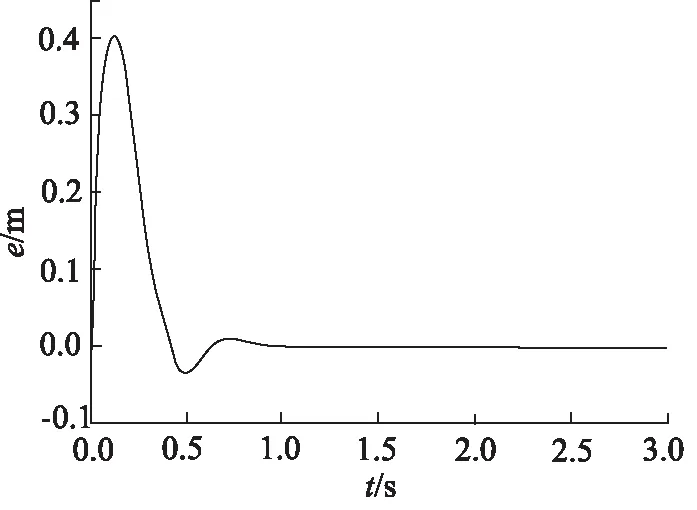
圖7 “串聯型”控制同步誤差(活塞桿伸出)

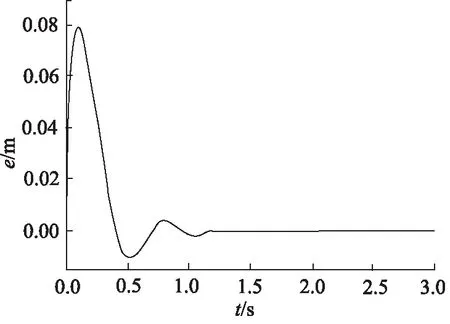
圖8 “并聯型”控制同步誤差(活塞桿伸出)

同樣的，對系統施加階躍信號，階躍后的值設置為-1，活塞桿縮回狀態下運行仿真結果如圖9～圖12所示。

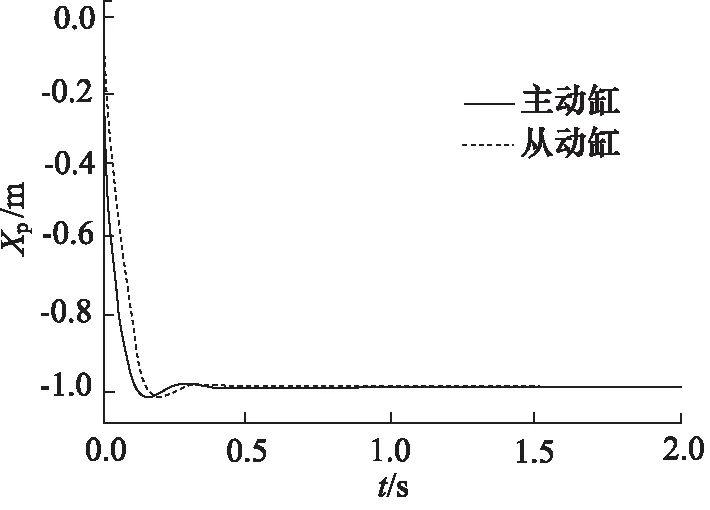
圖9 “串聯型”控制階躍響應曲線(活塞桿縮回)

不同控制結構下仿真結果對比，如表5所示。

由表5可得，在活塞桿縮回狀態下，“并聯型”相比“串聯型”最大同步誤差減小了88.03%；達到穩態同步誤差的調整時間增加了22.12%；2種控制結構下穩態同步誤差都為0。

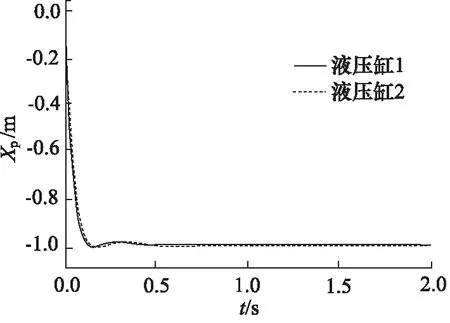
圖10 “并聯型”控制階躍響應曲線(活塞桿縮回)

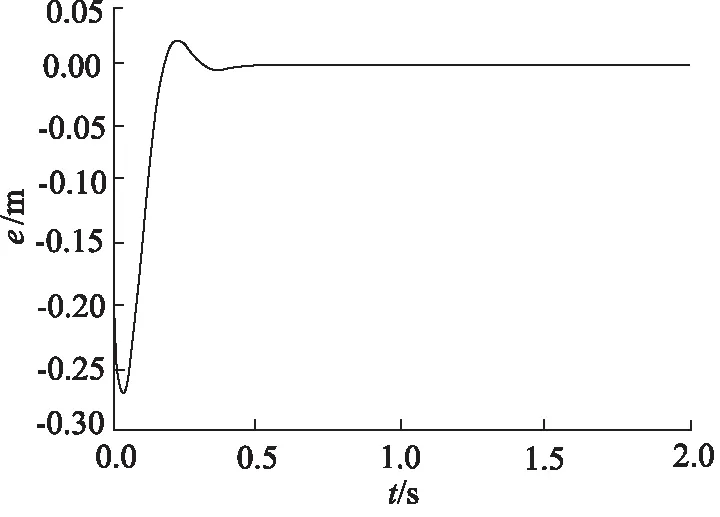
圖11 “串聯型”控制同步誤差(活塞桿縮回)

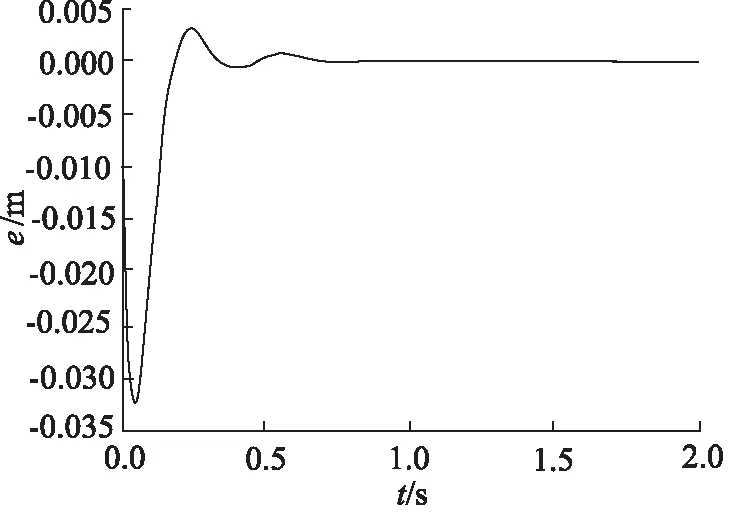
圖12 “并聯型”控制同步誤差(活塞桿縮回)

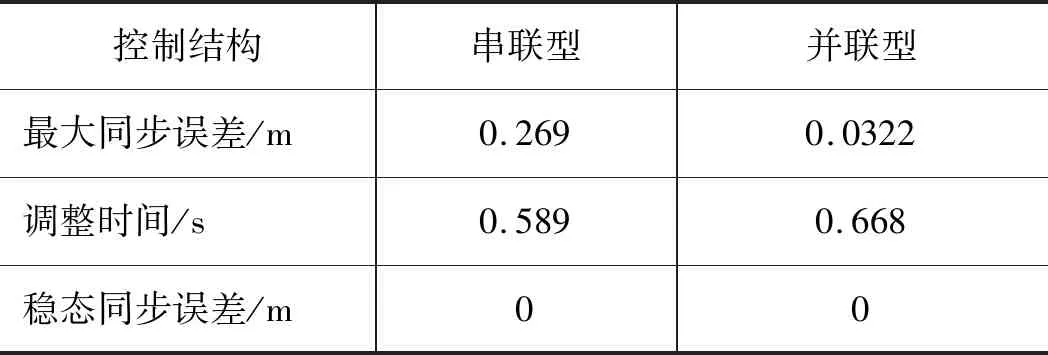
表5 2種結構下仿真結果對比(活塞桿縮回)

分析以上仿真結果可知，“并聯型”對于最大同步誤差的控制效果優于“串聯型”，但“并聯型”達到穩態同步誤差的調整時間長于“串聯型”，因此2種控制結構均存在缺點，無法滿足鍛造液壓機對于同步控制精度的要求。

為提高同步控制精度，采用一種誤差反饋的同步控制結構，如圖13所示。該控制結構在“串、并聯”控制結構的基礎之上，將液壓缸2的輸出位移與液壓缸1的輸出位移進行比較，并將同步誤差補償給反應速度較慢的液壓缸2使其動態響應加快，2缸位移差值減小，從而提高同步控制精度。

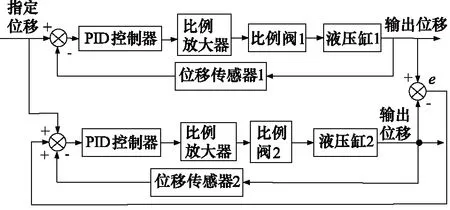
圖13 誤差反饋的同步控制結構

對系統施加階躍信號，活塞桿伸出狀態下2液壓缸階躍響應曲線和其同步誤差如圖14和圖15所示。

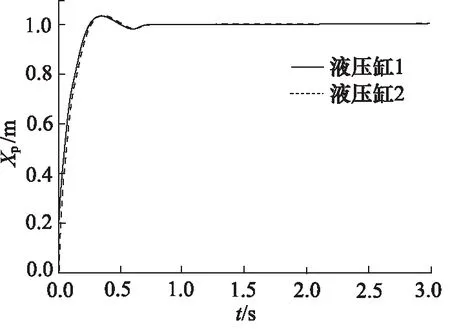
圖14 誤差反饋控制階躍響應曲線(活塞桿伸出)

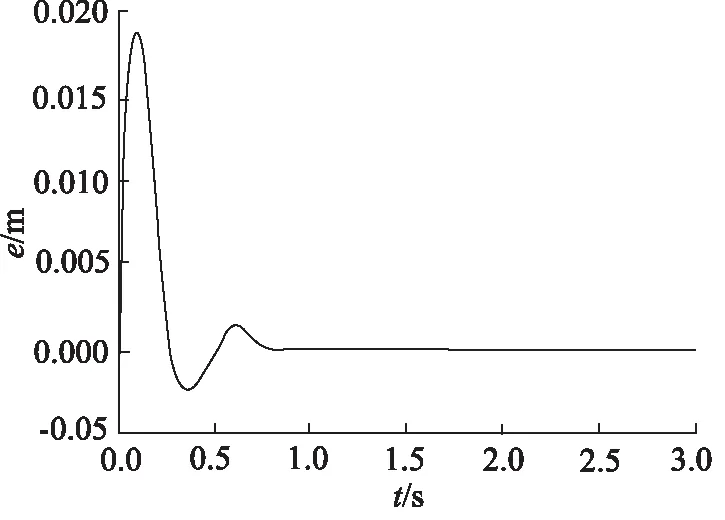
圖15 誤差反饋控制同步誤差(活塞桿伸出)

同樣的，對其系統施加階躍信號，活塞桿縮回狀態下2液壓缸的階躍響應曲線和其同步誤差如圖16和圖17所示。

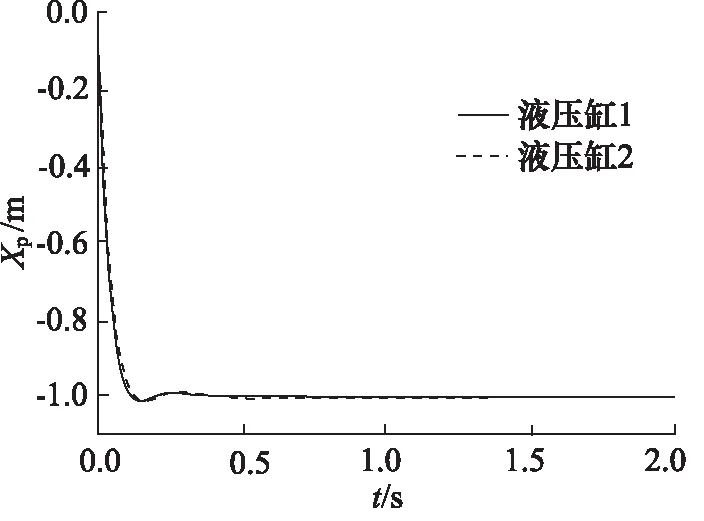
圖16 誤差反饋控制階躍響應曲線(活塞桿縮回)

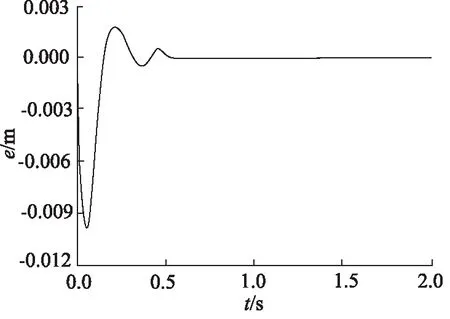
圖17 誤差反饋控制同步誤差(活塞桿縮回)

2種活塞桿狀態下系統性能指標，如表6所示。

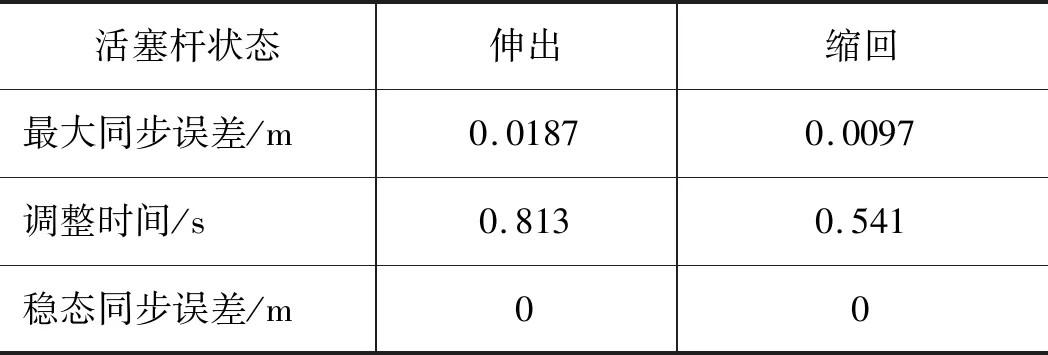
表6 2種活塞桿狀態下系統性能指標

由表4～表6可得，在活塞桿伸出狀態下，所采用同步控制結構相比“串聯型”和“并聯型”控制結構最大同步誤差分別減小了95.37%和76.42%；達到穩態同步誤差的調整時間分別縮短了18.94%和39.51%。在活塞桿縮回狀態下，誤差反饋同步控制結構相比“串聯型”和“并聯型”控制結構最大同步誤差分別減小了96.39%和69.94%；達到穩態同步誤差的調整時間分別縮短了7.36%和19.61%。并且伸出和縮回狀態下的穩態誤差均為0。從以上數據對比看出，采用同步控制結構能夠滿足鍛造液壓機同步控制要求。

4 結論

為實現鍛造液壓機雙缸的同步精確調整，設計了鍛造液壓機雙缸同步控制系統。在“串、并聯”控制結構基礎之上，采用了誤差反饋的同步控制結構，將仿真結果與“串、并聯”控制結構仿真結果進行了對比，主要得出以下結論：

在活塞桿伸出狀態下，誤差反饋同步控制結構相比“串聯型”和“并聯型”控制結構最大同步誤差分別減小了95.37%和76.42%；達到穩態同步誤差的調整時間分別縮短了18.94%和39.51%；穩態同步誤差分別減小了93.51%和85.40%。在活塞桿縮回狀態下，誤差反饋控制結構相比“串聯型”和“并聯型”最大同步誤差分別減小了96.39%和69.94%；達到穩態同步誤差的調整時間分別縮短了7.36%和19.61%；穩態同步誤差分別減小了87.23%和71.15%。從以上數據對比看出，采用同步控制結構能夠滿足鍛造液壓機同步控制要求。