基于CFD和FSI的擺線泵仿真分析

黃龍龍，王艷華，劉 勇,，徐勁松

(1.中北大學 能源動力工程學院，山西 太原 030051；2.中國兵器工業內蒙古第一機械制造(集團)有限公司，內蒙古自治區 包頭 014030)

引言

擺線內嚙合齒輪泵結構緊湊、體積小、轉速高，且具有運動平穩、噪聲低、容積效率較高的特點，適用于燃油系統中的傳輸、加壓、噴射的燃油泵以及航空航天、車輛等絕大多數工程領域的潤滑泵.國內外學者在幾何學、運動學與動力學特性和數值仿真等方面開展了大量研究工作。在擺線齒廓方面，SAEGUSA Y等[1]介紹了擺線機油泵轉子齒廓的形成。FABIANI M等[2]采用微積分方法定量計算齒間容積，并對配流盤幾何參數進行了設計計算。徐學忠[3-4]、LIU H等[5]應用復數矢量方法，推導出擺線泵內轉子的齒廓曲線方程。HWANG YW等[6]提出了提高泵效率的數學模型，推導了不產生根切的條件。在CFD仿真方面，陸鈞成等[7]基于CFD對水泵進行優化。徐剛[8]建立了擺線泵模型并對其進行數值模擬。RUNDO M[9]對機油泵進行流體動力學仿真，研究不同轉速下泵的性能。FROSINA E等[10]使用PumpLinx對Aprilia公司的一種高性能摩托車發動機的油泵進行仿真分析。KUMAR M S 等[11-12]分析了無污染油在室溫和高溫下模擬了轉子轉速、流體黏度、流道數等重要參數對泵流量的影響。王錚等[13]分析了發動機供油系統壓力脈動。為了提高仿真的真實性，GAMEZ-MONTERO P J等[14]和CASTILLA R等[15]采用接觸點黏度模型模擬齒輪之間的固-固接觸。大多學者采用CFD方法研究擺線泵不同結構、不同工況等下泵的性能，未考慮FSI方法對仿真結果的影響。在流固耦合研究方面，RUGONYI S等[16]用COMSOL多物理方法研究蠕動泵的流體結構相互作用。TAKASHI N等[17]和SARRATE J等[18]采用任意拉格朗日-歐拉方法，將剛體與流體的界面條件結合起來，描述了流體與剛體在平移和旋轉運動下的運動方程。以上學者采用流固耦合方法分析，并描述了流固耦合原理和對仿真結果的影響。

目前在擺線泵數值模擬方面，多數研究基于CFD對不同運行工況(如轉速、溫度等)下的泵進行分析，未考慮在流固耦合作用下泵的特性。首先基于COMSOL建立了擺線泵的模型，對流固耦合界面進行設置，設置相應的邊界條件后對泵進行CFD和FSI仿真，在流量和壓力特性方面與試驗結果進行對比，并將CFD和流固耦合進行詳細分析，得出更接近真實的擺線泵分析方法，更有利于對泵的流場和轉子動力學特性進行分析。

1 擺線泵模型

1.1 擺線泵模型參數

擺線泵由2個主要部件組成：1個內轉子和1個比內轉子多1個齒的外轉子。內轉子中心線與外轉子中心線之間的固定偏心距a。當轉子旋轉時，流體被吸入到旋轉油腔中，達到最大容積后隨著旋轉的繼續，腔室容積減小，迫使液體流出腔室。被測試泵的性能如表1所示。

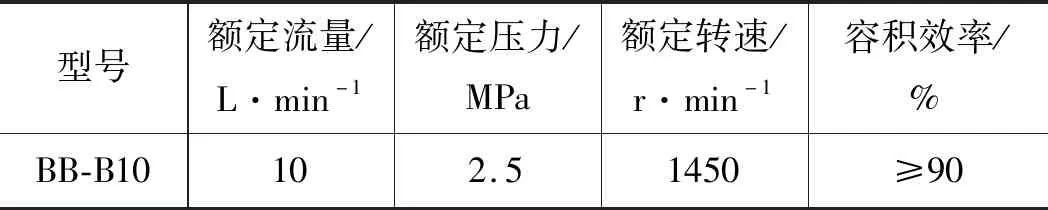
表1 被測試泵的性能

為了與試驗進行對比，建立了滿足相應性能的模型，表2為擺線泵幾何參數的取值。

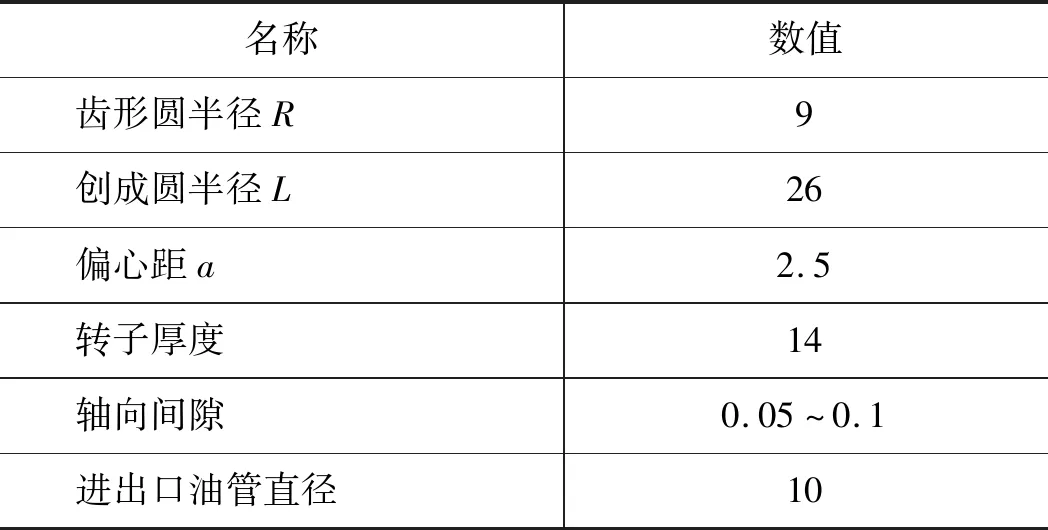
表2 擺線泵幾何參數 mm

1.2 搭建擺線泵試驗臺

1) 試驗臺搭建思路及操作

試驗臺構成如下：通過聯軸器2將電機1、扭矩儀3、泵軸4連接起來，從而電機帶動泵運轉的同時可以通過扭矩儀測試轉速和扭矩等；將油箱11通過油管與泵的進口進行連接，將泵的出口與油箱連接使得潤滑油在運行過程中循環使用；在泵的出口安裝壓力表5-1和壓力變送器6-1，來采集泵出口處的壓力，同時在泵出口安裝節流閥9比例溢流閥10，來對出口壓力進行調節；在節流閥出口處安裝壓力表5-2和壓力變送器6-2測試節流閥出口處壓力，同時在節流閥出口處安裝渦輪流量計來測試泵出口處流量。

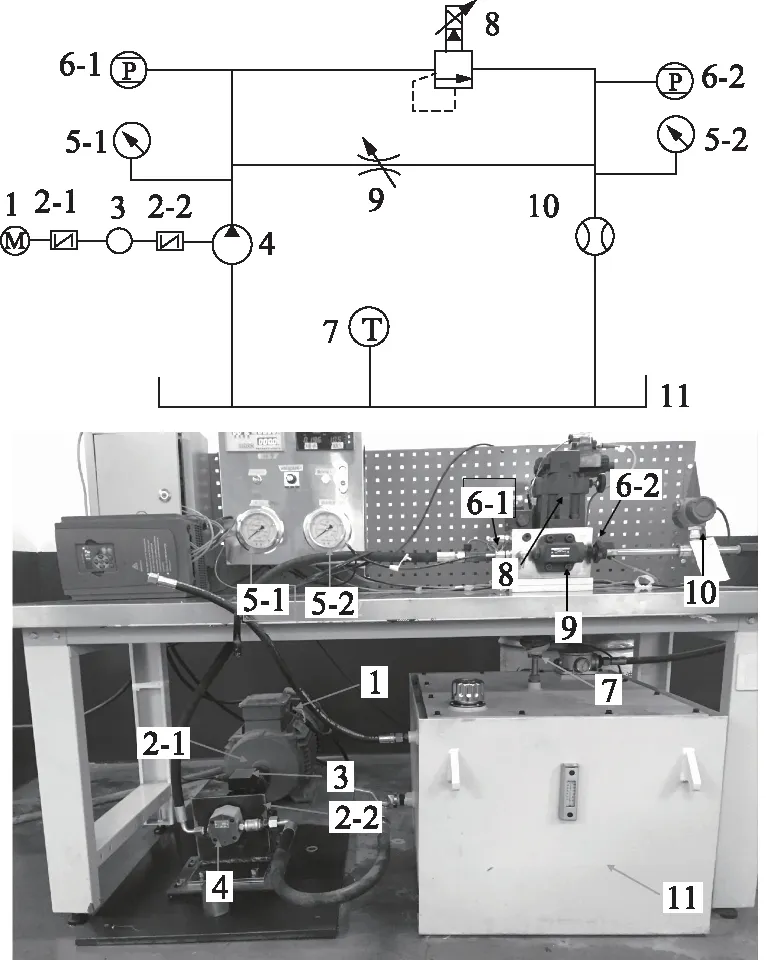
1.變頻電機 2.聯軸器 3.轉矩轉速傳感器 4.被測試機油泵 5.壓力表 6.壓力傳感器 7.溫度傳感器 8.溢流閥 9.節流閥 10.流量傳感器 11.油箱圖1 測試試驗臺連接圖

2) 操作流程

試驗過程中基本操作流程：打開節流閥，使出口壓力處于低壓狀態； 啟動電機，讓泵運轉一段時間，在流量、壓力、溫度穩定以后進行下一步；調節變頻器，使通電機轉速為指定測試條件下的轉速；調節節流閥，改變泵出口壓力；觀察流量壓力特性曲線，并采用LabVIEW進行數據采集。

2 擺線泵數值分析

2.1 擺線泵CFD仿真分析

在對擺線泵進行CFD數值模擬時，需要對流體域進行建模，流體域主要包括內外轉子間的旋轉區域、軸向泄漏區域、進出油腔和進出油管道，旋轉區域和泄漏區域受轉子的影響產生運動，其幾何形狀發生變化；進出油腔和進出油管為靜止流體域，詳細模型圖如圖2所示。

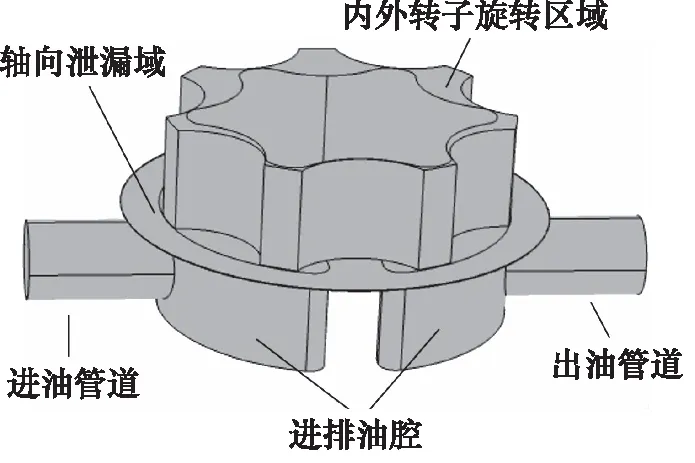
圖2 擺線泵流體域模型

1) CFD基本原理

(1) 流體中某一點的非定常三維質量守恒或連續性方程如下：

(1)

(2) 慣性(非加速)參考系中的動量守恒:

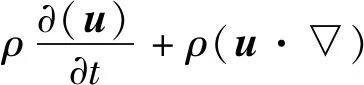
=▽·[-pI+μ(▽u+(▽u)T)]+F

(2)

式中，ρ—— 流體密度，kg/m3

p—— 靜態壓力，Pa

T—— 流體溫度，K

u—— 速度矢量，m/s

F—— 體積力矢量，N/m3

2.2 流固耦合基本原理

在ALE (Arbitrary Lagrange-Euler)公式中，從拉格朗日到歐拉變換，我們可以通過任意指定參考點的速度分布來任意選擇描述控制方程。不可壓縮流動的動量守恒定律和連續方程在參考描述中表述如下：

(3)

式中,σ—— 應力張量，Pa

uf—— 空間坐標系下材料粒子的速度矢量，m/s

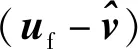
2) 結構運動方程

(4)

式中，ρs—— 材料密度,kg/m3

d—— 結構位移矢量,m

σs—— 二次Piola-Kirchhoff應力，Pa

Fb—— 體積力矢量,N/m3

3) 流固耦合方程

在流體-結構界面上Гf-s，當黏性流體與固體相互作用時，流體-結構界面必須滿足平衡和相容條件。這些條件是：

σ×n=σs×n

(5)

在Гf-s上，n是垂直于邊界的法向矢量，流體施加在固體邊界上的總力等于流體所受反作用力的負數，在Гf-s上流體的運動由固體傳遞而來，網格節點的速度需要滿足連續性條件。

通過FSI的理論分析得出：在耦合界面上, 流體動力及固體的運動事先都不知道, 只有在系統地求解了整個耦合系統后, 才可給出它們的解答, 這正是相互作用的特征所在，也是與CFD的不同之處，若沒有這一特征, 其問題將失去耦合作用的性質。

圖3為流固耦合仿真時建立的模型，表3為流體和固體的物理參數。

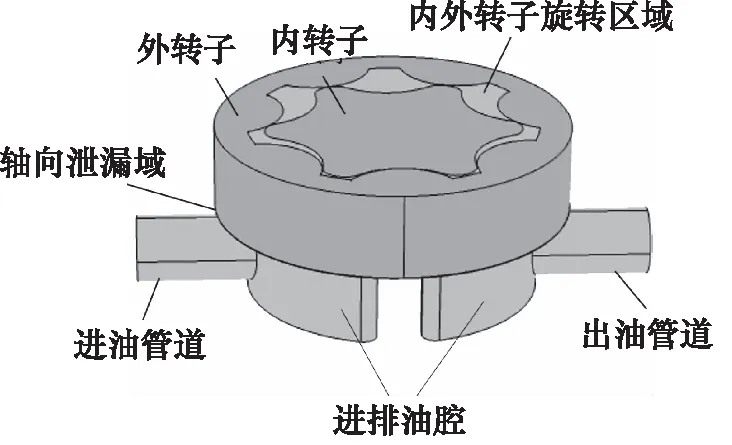
圖3 FSI仿真模型

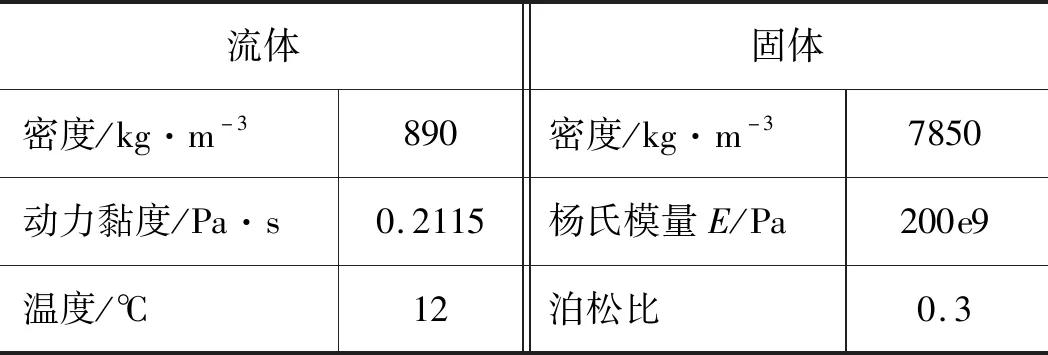
表3 流體和固體基本物理參數

2.3 邊界條件設置及網格劃分

1) 邊界條件設置

(1) 流體區域邊界條件

對于流體域具體邊界條件設置為進口為當地大氣壓，出口為0～2.5 MPa，靜態區域與動態區域采用一致對，保證數據傳遞，動態變形域采用ALE動網格方法，具體邊界條件設置如表和圖所示。對于流固耦合仿真指定內外轉子的運動及流體與固體耦合界面，具體設置如圖4所示。

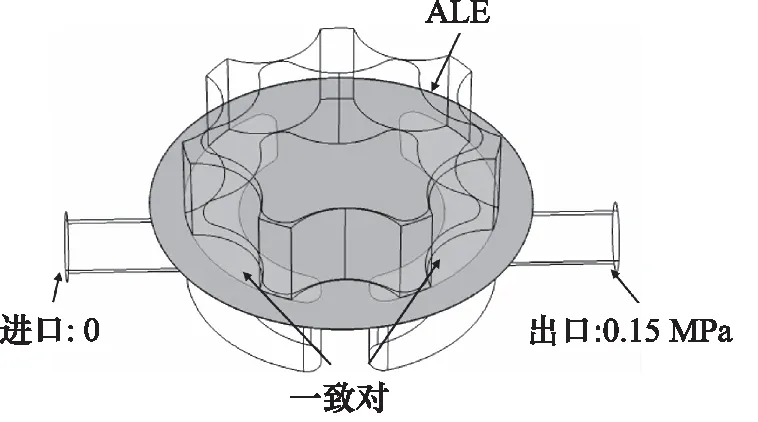
圖4 流體域邊界條件設置

(2) 流固耦合區域設置

圖5為內外轉子與之間的流體與耦合界面，在界面處將產生流固耦合作用。

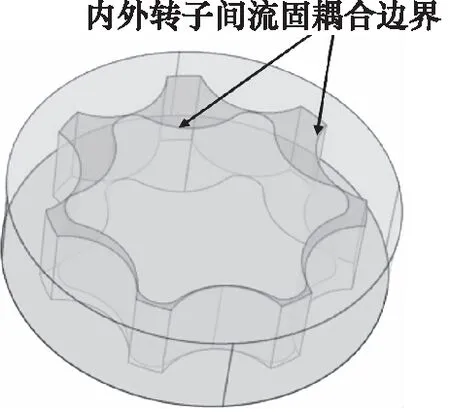
圖5 流體與固體耦合界面

2) 網格劃分

旋轉區域內外轉子間存在0.1 mm的間隙，因此應當設置最小網格尺寸為0.01 mm，最大網格尺寸不能過大，對旋轉區域和泄漏區域采用掃掠網格，其他靜止流體域采用自由四面體網格，具體網格如圖6～圖8所示。

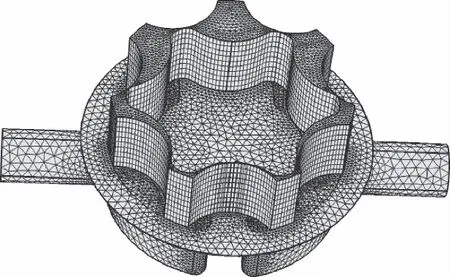
圖6 流體域網格劃分

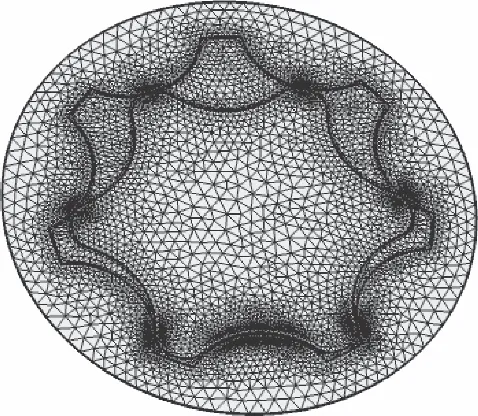
圖7 軸向泄漏區域網格劃分

圖8 流固耦合轉子與旋轉流體網格

3 CFD，FSI和試驗對比分析

3.1 出口流量和壓力特性對比分析

通過分析CFD和FSI仿真出口處的流量和壓力特性曲線，并與試驗結果進行對比，如圖9、圖10所示為CFD，FSI和試驗的對比。

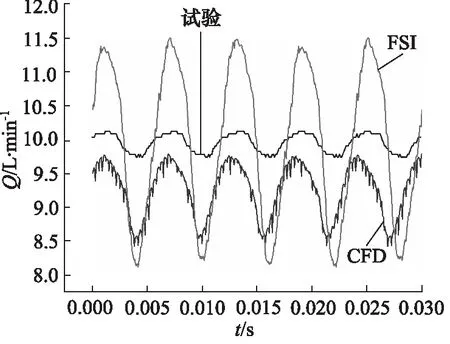
圖9 出口處瞬時流量波動分析

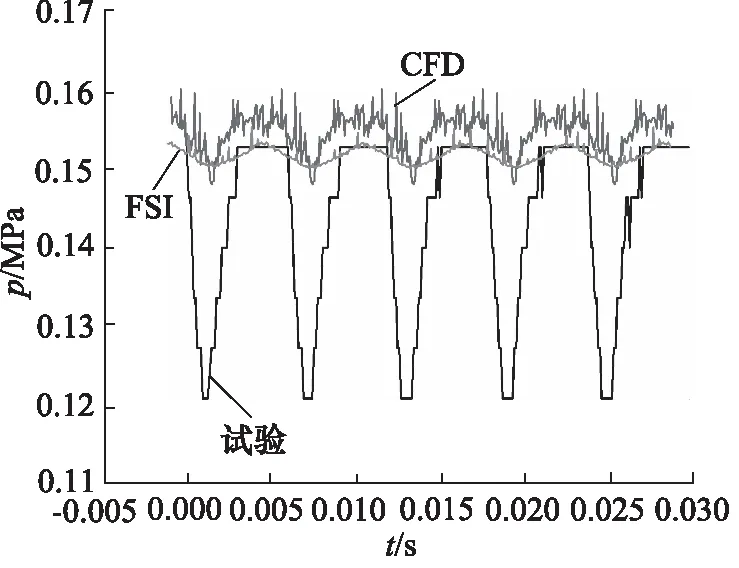
圖10 出口處瞬時壓力波動

對CFD，FSI和試驗的流量、壓力的平均值進行分析，式(6)為流量、壓力的平均值計算公式，表4和表5為具體的計算結果，并對比了CFD和試驗與FSI的誤差。

(6)

式中,Qm,pm—— 平均流量，平均壓力

Qsh，psh—— 瞬時流量，瞬時壓力

δQ，δP—— 流量脈動，壓力脈動

通過圖9、圖10、表4和表5分析，可以得出：

(1) 在流量特性方面：FSI的仿真的流量平均值均高于試驗和CFD的結果，更接近于試驗值，在CFD計算中，內外轉子與流體接觸界面，只指定了旋轉位移，而轉子在旋轉過程中將慣性力施加于流體，造成CFD計算結果低于試驗值；FSI出口處流量脈動率最大，由于試驗中出口采用較長的橡膠管，而且經過了節流閥、溢流閥這些部件，且試驗測試存在誤差，導致流量波動非常小；

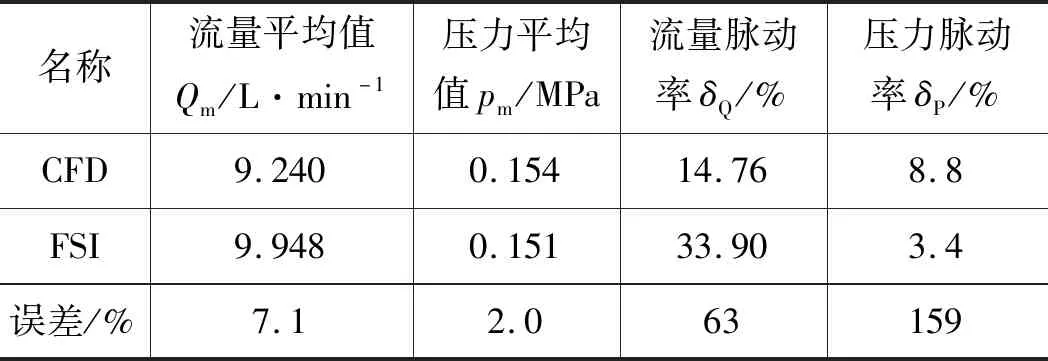
表4 CFD和FSI流量壓力特性對比分析

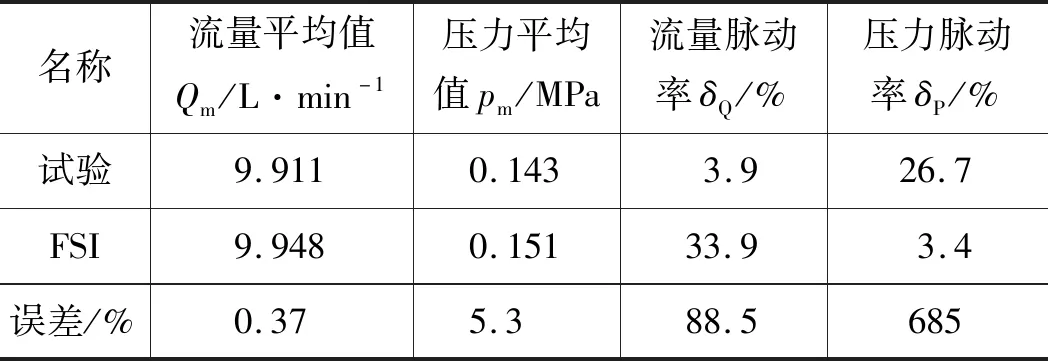
表5 試驗和FSI流量壓力特性對比分析

(2) 在壓力特性方面：FSI和試驗的出口壓力平均值均低于CFD的仿真值，FSI的壓力均值更接近CFD的結果，出口處壓力邊界條件為0.15 MPa，因此CFD和FSI的結果更合理；對比三者的壓力波動情況，CFD和FSI的壓力脈動率比較小，由于試驗過程中管路復雜且流過節流閥、溢流閥等部件以及壓力傳感器存在誤差，導致試驗測試的出口處壓力脈動率較大。

綜合以上分析得出：由于數值模擬、試驗均存在誤差，試驗、CFD和FSI結果存在差異，在流量方面FSI更接近試驗，在壓力方面FSI和CFD更符實際情況。結合FSI的理論分析得出：由于泵在運轉過程中轉子驅動流體運動從而產生流體和固體的相互作用，由于CFD在運動界面上只指定了運動，而FSI在流固耦合界面處流體不僅產生運動，而且受到固體的作用力，耦合對計算結果有很大的影響，因此FSI的仿真更接近實際。

3.2 CFD和FSI對比分析

為了研究耦合對計算結果產生的影響，進一步分析CFD和FSI的差異性，選擇CFD和FSI的旋轉流體域某截面(Z=7 mm)，由于CFD和FSI的流量壓力都是周期性波動，選擇1個周期來對比CFD和FSI仿真結果，如在0.015～0.022 s間選擇6個時間節點，對比壓力和速度的分布。如圖11和圖12分別為截面壓力和速度的對比圖。

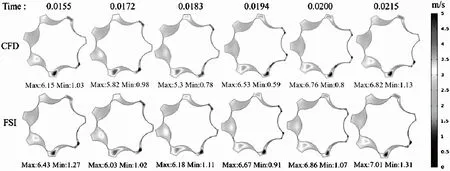
圖11 CFD和FSI旋轉域某截面速度分布對比分析

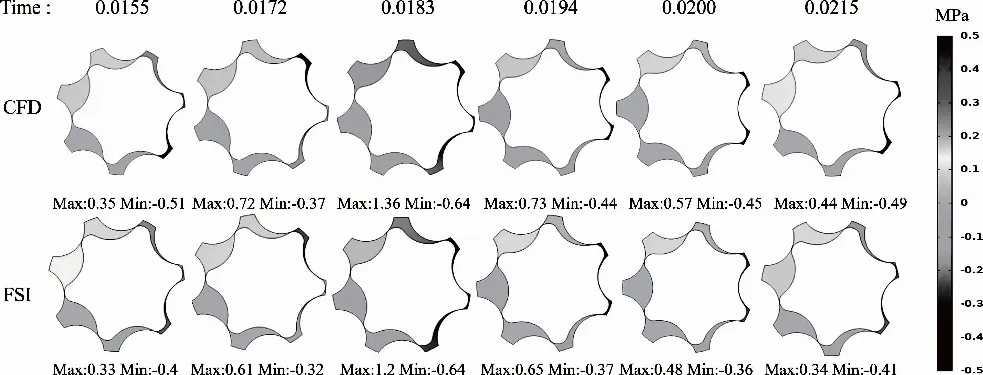
圖12 CFD和FSI旋轉域某截面壓力分布對比分析

通過圖11和圖12中壓力、速度云圖及最大值最小值分析得出：在吸油區域計算得到的負壓CFD大于FSI，計算得到的速度CFD小于FSI；在排油區計算得到的正壓力CFD大于FSI，計算得到的速度CFD小于FSI的結果。

進一步對內外轉子與流體接觸的區域進行對比分析。圖13a、圖13b分別為內外轉子某點處壓力隨時間的變化情況。

通過圖13a和圖13b內外轉子某點壓力變化得出：CFD在內外轉子表面上一點處的壓力值均大于FSI的壓力值，產生這種差異的主要原因是在FSI中由于固體的慣性力作用于流體從而改變了流體的運動狀態，流體的速度增大，從而壓力減小。

綜合以上分析得出：耦合對計算結果有很大的影響，由于CFD在轉子流體交界面處指定了位移運動，從而確定了邊界處的速度，而流固耦合存在轉子與流體的相互作用，由于轉子幾乎不變形，因此不考慮彈性力的作用，但轉子在高速旋轉，存在慣性力，通過交界面將慣性力施加于流體，從而改變流體的運動狀態，從而增加了流體的速度降低了流體的壓力。

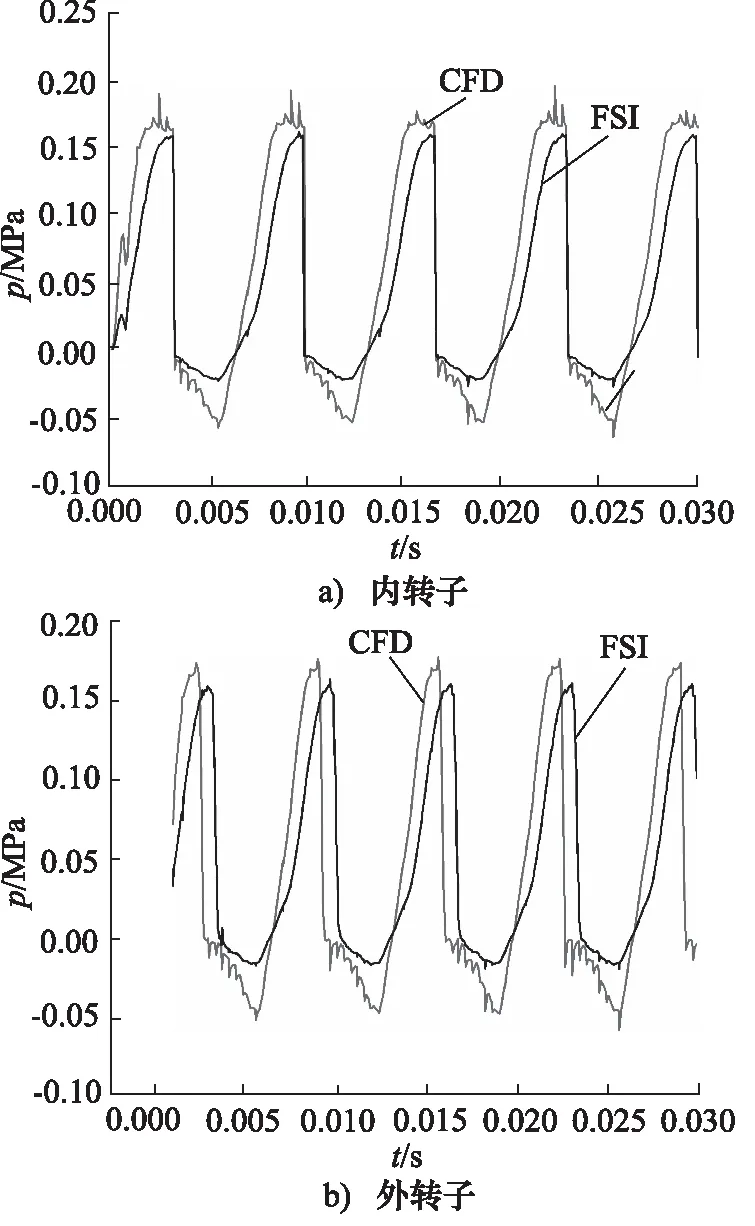
圖13 內外轉子表面某點的壓力分布

4 結論

通過建立擺線泵模型，根據CFD和FSI的基本原理，設置相應的邊界條件和劃分網格后對擺線泵進行CFD和FSI仿真分析，并于試驗結果進行對比，研究結果表明：

(1) 在流量特性方面：FSI的仿真的流量平均值更接近于試驗值在壓力特性方面：FSI和CFD的出口壓力平均值更符合實際，試驗出口壓力均值略低。結合對比分析和FSI理論得出FSI的仿真更接近真實；

(2) 通過對比內外轉子間流體域某一截面速度和壓力得出：在吸油區域計算得到的負壓CFD大于FSI，計算得到的速度CFD小于FSI；在排油區計算得到的正壓力CFD大于FSI，計算得到的速度CFD小于FSI的結果；

(3) 通過對比內外轉子與流體耦合界面某點處的壓力分布得出：CFD的壓力隨時間的波動值均大于FSI的壓力值。

綜合以上分析得出：CFD和FSI的計算結果均存在差異，由于CFD在運動界面上只指定了運動，而FSI在流固耦合界面處流體不僅產生運動，而且受到固體的作用力，通過對比發現耦合對計算結果有很大的影響，對泵進行FSI耦合分析使得分析結果更加真實，更有利于對泵的流場和轉子動力學特性進行分析。