金茲堡-朗道方程組的整體吸引子

劉 帥，陳淑紅

（閩南師范大學數學與統計學院，福建漳州363000）

整體吸引子是無窮維動力系統研究的重要內容，對于揭示系統解的長時間行為具有重要的意義.本文主要研究BEC - BCS跨越模型在有外力作用時，所得到的依賴于時間t的金茲堡-朗道方程組整體吸引子的存在性.

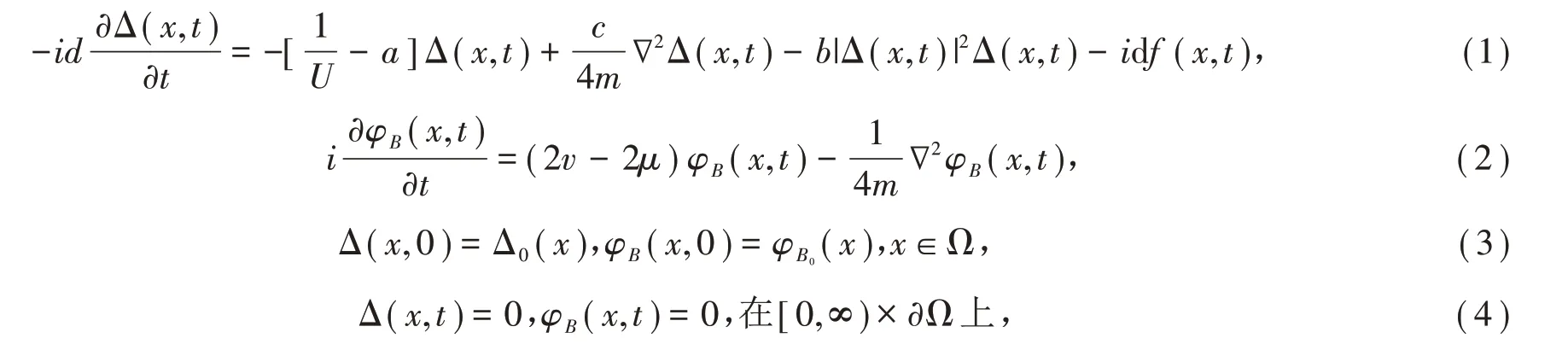
Henry[1],Roger[2]對金茲堡-朗道理論及整體吸引子的研究取得了長足的進步.Schakel[3]利用導數展開法從微觀BCS模型中推導出具有時間依賴性的金茲堡-朗道理論；Drechsler等[4]推導出金茲堡-朗道理論去描述BCS 超導性與玻色凝聚的跨越；Machid 等[5]研究了BEC - BCS 跨越附近原子費米子氣體的具有時間依賴性的金茲堡-朗道方程，證明了除BEC 限制外，具有時間依賴性的金茲堡-朗道方程的GL 系數是復數.Ghidaglia 等[6]和Promislow[7]在1 維和2 維空間研究了帶立方非線性項的金茲堡-朗道方程的有限維整體吸引子；郭柏靈[8]研究了廣義Kuramoto-Sivashinsky 型方程周期初值問題的整體吸引子；Sell[9]研究了3維Navier-Stokes 方程整體吸引子的存在性；戴正德[10]研究了耗散KDV 型方程Cauchy 問題的動力學行為及整體吸引子的存在性.

基于以上的研究，本文致力于BEC - BCS跨越中帶外力項的金茲堡-朗道方程組的整體吸引子，并得到了以下結果.

1 引理

引理1[1]令1 ＜p ＜∞，若對于任意的u ∈C2()滿足

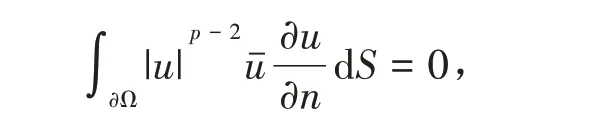
則有

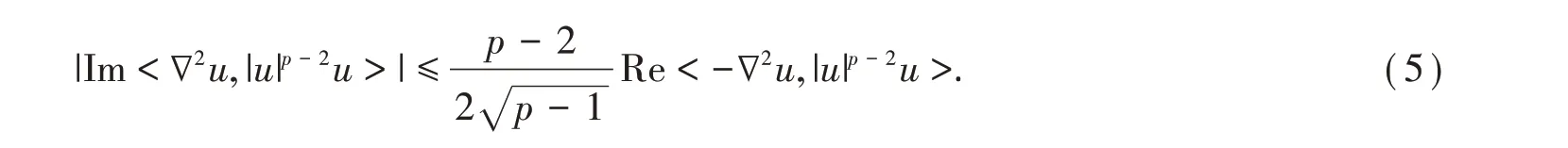
通常地，n表示邊界?Ω的外法向量.

由式(5)，可以推出

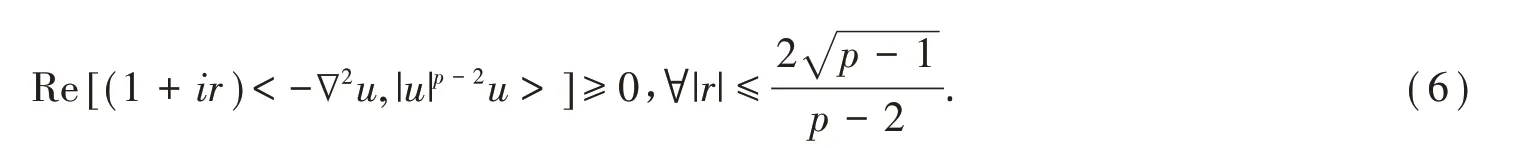
引理2[2]令E 是一個巴拿赫空間，{St,t ≥0}是一個半群算子，St:E →E，滿足St?Sτ= St+τ，S0= I，這里I是一個恒等算子，且假定算子半群St滿足如下條件：

1)算子St在E 上是一致有界的，即對于任意的R ≥0，存在一個常數C(R)，使得當||u?||E≤R 時，對于任意的t ∈[0,∞)，有||Stu?||E≤C(R);

2) 存在一個E 上的有界吸收集B0，即對于任意的有界集B ?E，存在一個常數T，使得當t ≥T 時，有StB ?B0;