三類乘積圖的peripheral Wiener指標

董哈微

（閩江學院數(shù)學與數(shù)據(jù)科學學院，福建福州350001）

對于一個圖G,圖的點集和邊集分別記為V(G)和E(G).圖G的兩個頂點u,v之間的距離指的是在圖G中頂點u和頂點v之間的最短路的長度，記作dG(u,v)（不會產(chǎn)生混淆的話，簡記為d(u,v)）.對v ∈V(G)，頂點v 的離心率ε(v)= max{d(u,v),u ∈V(G)}. 圖G 的直徑為最大離心率，即d(G)=max{ε(v) |v ∈V(G}.peripheral 頂點集P(G)指圖G 中滿足ε(v)=d(G)的所有頂點. 用 ||P(G) 表示圖G 中peripheral 頂點的個數(shù).

乘積圖在許多領域，如人類遺傳學、動態(tài)選址問題、網(wǎng)絡問題等都扮演著重要角色[10].計算乘積圖的拓撲指標也成為許多學者的研究課題.其中，第一個對這個課題進行研究的是Graovac 和Pisansk[11]，他們計算的是乘積圖的Wiener 指標.稍后，Yeh 等[12]計算了在笛卡爾乘積、cluster 運算、連接運算、組合運算、corona乘積運算下的乘積圖的Wiener指標.Sagan等[13]引入連接、笛卡爾乘積、Disjunction、對稱差、張量積這6 種圖運算，并計算出對應的乘積圖的Wiener 多項式的公式.在文獻[14]中，Kahsay A 和Narayankar K已經(jīng)給出一些經(jīng)典的乘積圖的peripheral Wiener指標的計算公式.本文繼續(xù)探討這個問題，給出corona乘積、disjunction和對稱差這3種運算的乘積圖的peripheral Wiener指標的計算公式.

'

1主要結(jié)論

1.1 corona乘積圖的公式

corona 乘積是一個常用的圖運算[12].設G1和G2為兩個圖，拷貝 ||V(G1) 個G2，連接G1中的第i 個頂點和G2的第i 個拷貝中的每個頂點，其中i = 1,2,…, ||V(G1) ，得到的圖為圖G1和圖G2的corona 乘積圖，記為G1°G2.

1.2 Disjuction乘積圖的公式

1.3 對稱差乘積圖的公式

圖G1和圖G2的對稱差乘積圖[16]，記為G1⊕G2. 其是一個圖，滿足頂點集為V(G1)×V(G2)，并且點(v1,v2)和(u1,u2)相鄰當且僅當u1v1∈E(G1)或u2v2∈E(G2)，但兩者并不同時成立.定理3 設G1，G2是簡單連通圖，則

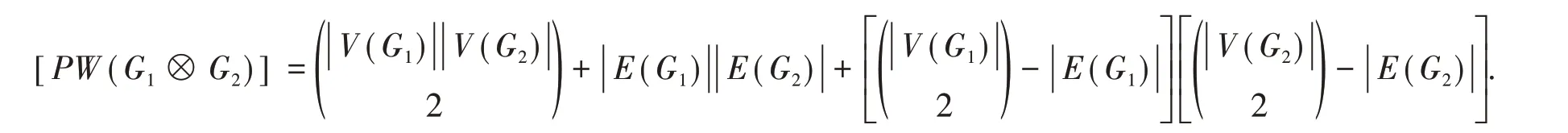
證明 計算可得，G1⊕G2有 ||V(G1)2||E(G2) + ||V(G2)2||E(G1)-2 ||E(G1) ||E(G2) 條邊.任取點(u1,u2),(v1,v2)∈V(G1⊕G2).

情況1：u1v1∈E(G1)且u2v2?E(G2)或者u1v1?E(G1)且u2v2∈E(G2).

由G1⊕G2的定義，得d((u1,u2),(v1,v2))= 1.

情況2：u1v1∈E(G1)且u2v2∈E(G2).

由G1⊕G2的 定……