數(shù)學(xué)實驗，從問題開始

王興偉

【摘要】數(shù)學(xué)實驗是一種有效的數(shù)學(xué)建構(gòu)過程和探究活動，它鼓勵學(xué)生發(fā)現(xiàn)和提出問題。本文從情境提問、問題還原、問題組塊、反思拓展、激勵評價等五個方面闡述了如何在數(shù)學(xué)實驗中恰當(dāng)?shù)匾龑?dǎo)學(xué)生發(fā)現(xiàn)和提出問題，從而有效地提高學(xué)生的問題意識，全面提升學(xué)生核心素養(yǎng)。

【關(guān)鍵詞】數(shù)學(xué)實驗 問題 策略

數(shù)學(xué)實驗是新課改后一線教師使用較廣的一種方法，一個完整的數(shù)學(xué)實驗主要包括“發(fā)現(xiàn)和提出問題、猜想或假設(shè)、設(shè)計和進行實驗、分析和得出結(jié)論”等環(huán)節(jié)。數(shù)學(xué)課程標(biāo)準(zhǔn)提出：“要讓學(xué)生在提出問題、分析問題、解決問題的過程中自主學(xué)習(xí)，享受學(xué)習(xí)的快樂。”那么如何在數(shù)學(xué)實驗中恰當(dāng)?shù)匾龑?dǎo)學(xué)生發(fā)現(xiàn)和提出問題，使學(xué)生敢問、會問、善問呢？筆者在以下幾方面做了嘗試：

一、情境提問——因果策略

要培養(yǎng)學(xué)生的問題意識，首先必須激起學(xué)生的興趣。創(chuàng)設(shè)趣味性的教學(xué)情境，促使學(xué)生自主、自愿地去想、去問，并且樂在其中。情境中蘊含著豐富的數(shù)學(xué)信息與問題，應(yīng)用情境提問的策略就是讓學(xué)生從情境中整理信息，提出要解決的問題，繼而引導(dǎo)學(xué)生思考“為什么設(shè)置這樣的情境”，從而去解決問題。

【案例1】 圓的認(rèn)識

上課伊始，教師設(shè)計了一個與學(xué)生比賽的實驗情境：全班挑選兩個平時數(shù)學(xué)成績最好、能力最強的學(xué)生，在黑板上用一個點固定一根線，老師和學(xué)生一起畫圓，比賽誰畫得又快又好。在全體學(xué)生熱烈的加油聲中，學(xué)生發(fā)現(xiàn)老師雖然慢條斯理卻很快就畫出了一個漂漂亮亮的圓，而全班選出的數(shù)學(xué)成績最好的兩個學(xué)生用了很長一段時間，始終畫不出完整的圓。見此情景，有細(xì)心的學(xué)生很快發(fā)現(xiàn)了問題，大聲提出“比賽不公平”，老師微笑問他為什么。學(xué)生拿起剛才的畫圓工具說：“我們拿著的線是可以伸縮的，在畫的過程中不能固定其長度。”教師由此引導(dǎo)學(xué)生思考，學(xué)生提出了一連串問題：“畫圓為什么要固定一點”“這個點與圓有什么關(guān)系”“畫圓的線為什么要不能伸縮”“不同長度的線畫出的圓是什么樣子”？在這種真實有趣的比賽情境中，隱含著對數(shù)學(xué)本質(zhì)的探究。學(xué)生在這樣的情境中，用數(shù)學(xué)的眼光發(fā)現(xiàn)數(shù)學(xué)問題，用數(shù)學(xué)的語言提出問題，問題意識不斷增強。

二、 問題還原——比較策略

研究表明，當(dāng)學(xué)生面對一個問題時，自覺或不自覺地會主動聯(lián)系其已有經(jīng)驗，利用其已有經(jīng)驗中的表征方式進行同化。在數(shù)學(xué)實驗中，可以讓學(xué)生充分比較同一數(shù)學(xué)規(guī)律在不同情境下的應(yīng)用，比較互相矛盾的解釋、說法和理論，從中發(fā)現(xiàn)并提出問題。用此策略，當(dāng)學(xué)生面對問題時，要充分調(diào)動其已有經(jīng)驗，對問題進行判斷或選擇，從而把問題還原到其已有的經(jīng)驗架構(gòu)內(nèi)，當(dāng)不同主體經(jīng)驗碰撞時產(chǎn)生矛盾沖突，自然就形成新的問題，促使學(xué)生一探究竟，深入研究。

【案例2】兩、三位數(shù)乘一位數(shù)筆算

在學(xué)習(xí)過兩、三位數(shù)乘一位數(shù)筆算例題后，學(xué)生得出基本算法：數(shù)位對齊，從個位乘起。這個規(guī)定，大多數(shù)學(xué)生只是機械地記住了算法。課堂上，一個學(xué)生提出了這樣的一個疑問：“兩、三位數(shù)乘一位數(shù)，要從個位開始乘起，如果從最高位開始乘，是不是結(jié)果就不一樣了呢？”聽到這個問題，筆者靈機一動，先讓學(xué)生猜猜看，結(jié)果發(fā)現(xiàn)有人認(rèn)為不一樣，有人認(rèn)為肯定一樣。

接著筆者提供了兩個算式：34×2和132×3，學(xué)生通過計算比較，很快驗證了猜想，得出了一致的結(jié)論：從個位乘起和從最高位乘起，結(jié)果一模一樣，而且都很方便。這時候，又有學(xué)生提出：“既然結(jié)果一樣，為什么還做這樣的規(guī)定？”

在教師的啟發(fā)下，大家紛紛建議，可以再寫幾個算式，自己試著再算一算。當(dāng)每個學(xué)生分別從個位算起和從最高位算起后，經(jīng)過比較，很快就發(fā)現(xiàn)問題了：“如果是不進位的乘法，隨便從個位還是最高位開始，都很方便;但是如果是進位乘法，從最高位開始乘就不方便了。”于是，“進位乘法”的法則學(xué)生們通過計算實驗，已經(jīng)很明白了。通過比較，學(xué)生們不但知其然，并且知其所以然，為他們發(fā)現(xiàn)問題、解決問題提供了可能。

三、問題組塊——擴大策略

數(shù)學(xué)實驗中，教師要讓學(xué)生在活動中多想想會遇到什么問題、為什么會有這些問題以及怎么解決問題，使學(xué)生自覺地經(jīng)常把這些問題進行組塊，形成一個“問題場”，學(xué)生置身“問題場”中不斷得以浸染，在解決問題時，會不斷產(chǎn)生“怎么辦”“為什么這么辦”等主動意識。教師要不斷啟發(fā)學(xué)生思考：從這個現(xiàn)象中總結(jié)出的規(guī)律，推廣到更大范圍或一般情況還能成立嗎？這個規(guī)律是具有普遍性還是只適合于某些特殊情況？怎樣改動才可以應(yīng)用到另外的情況？教師在課堂教學(xué)中，要多問“為什么”，給學(xué)生表達思維過程的機會，培養(yǎng)學(xué)生的批判性思維，進而不斷發(fā)現(xiàn)問題，學(xué)會提問。

【案例3】釘子板上的多邊形

教師首先讓學(xué)生觀察圖1，提出問題：這4個多邊形的面積與每個多邊形邊上的釘子有什么關(guān)系？你能用一個關(guān)系式表達嗎？學(xué)生通過觀察、計算， 很快概括出規(guī)律：用S表示面積，n表示釘子數(shù)，S=n÷2。

然后教師呈現(xiàn)3幅圖，如圖2，讓學(xué)生數(shù)出它邊上的釘子數(shù)和面積數(shù)，快速驗證，并思考有什么問題。結(jié)果學(xué)生發(fā)現(xiàn)，前兩個符合這樣的規(guī)律，第三個不符合，從而產(chǎn)生新問題：為什么有的符合，有的不符合呢？經(jīng)過觀察比較，學(xué)生發(fā)現(xiàn)：這個規(guī)律必須滿足“內(nèi)部有a枚釘子，a=1”這個條件，也就是a=1時，S=n÷2才成立。

教師接著啟發(fā)學(xué)生：這個規(guī)律推廣到更大范圍還能成立嗎？讓學(xué)生分組研究多邊形里面有2枚釘子的規(guī)律。學(xué)生通過和小組成員先畫一畫、數(shù)一數(shù)、算一算，發(fā)現(xiàn)當(dāng)a=2時， S=n÷2+1，教師相機板書。

至此，學(xué)生的思維已經(jīng)被激活，他們馬上會思考：a=3有怎樣的規(guī)律？a=4呢？ a除了可以是1、2、3、4，還可以表示什么？有什么方法去驗證呢？學(xué)生通過分組實驗，很快驗證了這些結(jié)論。教師將這些公式一一進行板書，啟發(fā)學(xué)生：你能用一個式子將這么多式子概括出來嗎？學(xué)生通過抽象，自然得出：S=n÷2+a-1。

在以上的過程中，教師設(shè)計了層層遞進、環(huán)環(huán)相扣的問題組，由表及里，不斷地引領(lǐng)學(xué)生向數(shù)學(xué)規(guī)律的本質(zhì)挺進，學(xué)生在“提出問題—解決問題—又提出新問題—再解決問題”的循環(huán)往復(fù)中，充分經(jīng)歷了數(shù)學(xué)建構(gòu)的過程，感受到了數(shù)學(xué)學(xué)習(xí)的有趣好玩與挑戰(zhàn)性，點燃了思維的火花。

四、反思拓展——變化策略

每一次的數(shù)學(xué)實驗活動都是學(xué)生探究學(xué)習(xí)的“加油站”，每次活動的結(jié)束只是又把學(xué)生帶到另一個新的起點，因此教師對于每次實驗都要做好反思與拓展，讓學(xué)生能主動認(rèn)識到活動中存在的問題，以及為什么會出現(xiàn)這樣的問題。教師要經(jīng)常引導(dǎo)學(xué)生思考：在通常情況下成立的理論與規(guī)律，放到極端條件下還會出現(xiàn)或成立嗎？會不會出現(xiàn)新的問題？正面的問題，反過來會怎樣？這個結(jié)果還有沒有其他的結(jié)論？如果條件改變，結(jié)果會怎樣？從而不斷內(nèi)化認(rèn)識，積累并升華學(xué)生提出問題的經(jīng)驗。

【案例4】奇妙的百分率

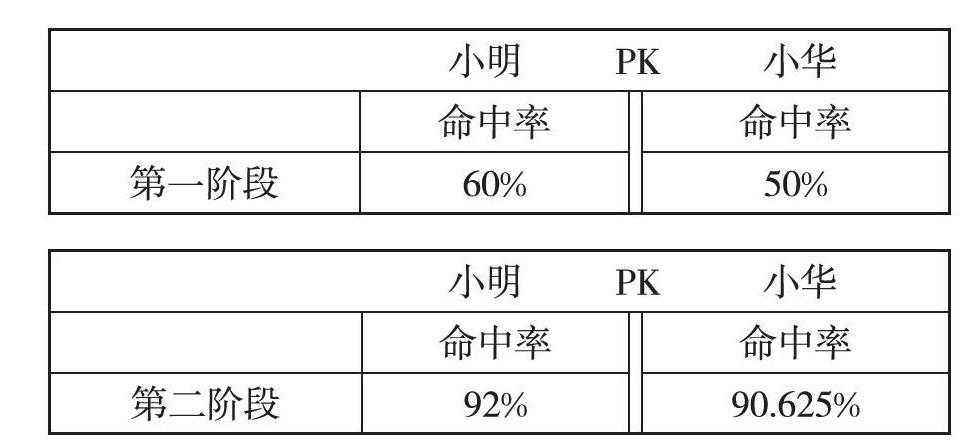
教師首先分別出示小明和小華第一階段和第二階段比賽的表格。讓學(xué)生觀察在第一階段和第二階段，誰的命中率高。學(xué)生觀察后得出：兩個階段，小明的命中率都比小華高。

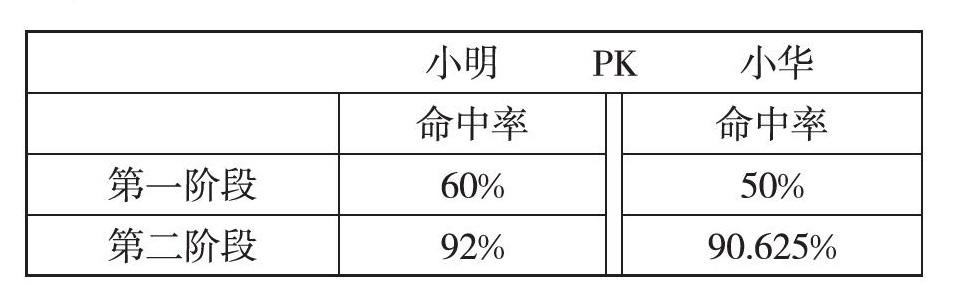
然后，教師將上面兩個表格合二為一，提出：將兩階段投籃的情況結(jié)合起來考慮，你認(rèn)為誰投籃的命中率高？這時，學(xué)生幾乎不假思索，一致都認(rèn)為：仍然是小明命中率高。只有個別學(xué)生表示懷疑，但也說不出理由。

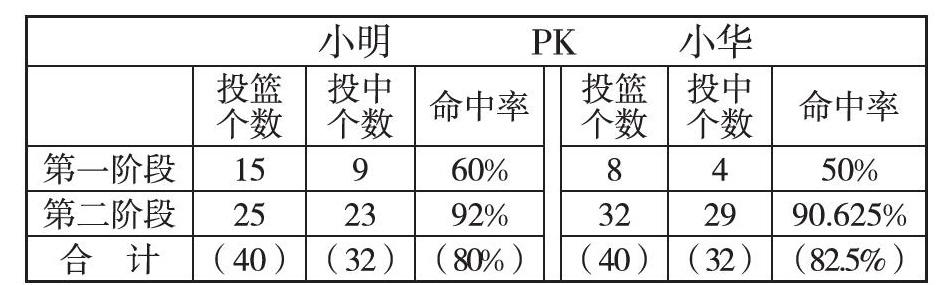
接著，教師完整出示如下表格，引導(dǎo)學(xué)生觀察后思考有什么問題。有了具體的數(shù)據(jù)支撐，學(xué)生馬上就提出：小華兩階段的投籃命中率都比小明低，總的投籃命中率卻超過了小明，這是為什么？

教師讓學(xué)生先將想法寫下來，在小組內(nèi)交流，再組織全班討論。通過交流，學(xué)生會發(fā)現(xiàn)：小華命中率低的時候投籃個數(shù)非常少，而命中率提高的時候投籃個數(shù)卻很多，小明兩次投籃的個數(shù)相差不大。階段比賽的單位“1”不同，僅靠這兩個階段的命中率不足以準(zhǔn)確判斷，只有比較總命中率才能正確判斷。

這里，當(dāng)學(xué)生的已有知識經(jīng)驗與眼前的情境發(fā)生沖突時，往往會引起學(xué)生的關(guān)注和探索，通常成立的規(guī)律，為什么放到這里不成立呢？此時學(xué)生在心理上產(chǎn)生填補這些空白的強烈欲望，教師及時抓住學(xué)生的迫切心理，讓學(xué)生自主探究，往往會收到超預(yù)期的教學(xué)效果，學(xué)生的問題意識會得到明顯的提升。

五、激勵評價——量化策略

美國心理學(xué)家羅杰斯認(rèn)為，“成功的教學(xué)依賴于一種真誠的理解和信任的師生關(guān)系，依賴于一種和諧安全的課堂氣氛。”教師要正確對待學(xué)生的提問，發(fā)掘其可貴之處，建立一套合適的激勵評價策略。

首先，教師要注意在師生間建立平等、民主、親切、和諧的關(guān)系，用風(fēng)趣、幽默的語言，親切和諧的笑容，為消除學(xué)生心理障礙創(chuàng)設(shè)良好氛圍。

其次，在課堂教學(xué)中，教師要做到當(dāng)學(xué)生提出的問題不符合要求時，教師也同樣要給予鼓勵;當(dāng)學(xué)生在提出問題的過程中，由于緊張或考慮不充分而詞不達意、語無倫次時，教師也要認(rèn)真傾聽，不能打斷學(xué)生的發(fā)言;當(dāng)學(xué)生提出錯誤的問題時，教師也不能嘲笑、諷刺、指責(zé)。一句話，要讓學(xué)生在課堂上能夠“自由地呼吸”，敢想、敢說、敢做，能充分表達自己的見解。

第三，教師可以設(shè)計一張表格，根據(jù)表格中學(xué)生的行為，定期請小組互評，作為平時成績評定的依據(jù)。有了行為指標(biāo)，學(xué)生的行動就有了指南和方向。

1.能找出并提出問題

2.有不懂的問題能及時提出

3.敢于向老師提出問題

4.敢在集體場合發(fā)表自己的見解

5.對自己不理解、不知道的事物愛提出問題

6.提問時聲音響亮

7.預(yù)習(xí)新課，把不懂的問題記錄下來

8.對老師、同學(xué)的講述能根據(jù)自己的理解質(zhì)疑

9.對自己感到疑惑的地方不放過，能提有一定深度的問題

10.能在舊知的基礎(chǔ)上產(chǎn)生新的問題

在教學(xué)中，教師要根據(jù)學(xué)情和教材特點，靈活使用上述策略。在數(shù)學(xué)實驗活動中，教師還要充分引導(dǎo)學(xué)生在實驗中開展猜想、假設(shè)、實驗、比較、分析、論證、評估、交流等活動，這樣才能有效地激發(fā)學(xué)生發(fā)現(xiàn)問題、提煉問題、分析問題、解決問題的意識;強化學(xué)生“問題意識”，進而全面提升學(xué)生核心素養(yǎng)。