數學核心素養在2019年高考全國卷中的考查特點

蒙自市第四中學 浦仕宏 沈麗群

縱觀2019 年高考數學全國卷，我們不難發現，命題者在創新和立意上均下了不少功夫，出了不少新題.這些題目注重考查考生的閱讀和理性思維能力、綜合運用數學思想方法分析和解決實際問題的能力以及對數據的整理及求解能力，著力考查考生的數學核心素養.

一、合理設置問題情境，注重考查考生的閱讀理解能力和運算求解能力

2019 年的高考數學全國卷，結合數學學科的特點，合理設置問題情境，貼近實際生活，注重落實立德樹人的育人目的.

例1 （2019年高考全國Ⅱ卷理科第4題）2019 年1 月3 日，嫦娥四號探測器成功實現人類歷史上首次月球背面軟著陸，我國航天事業取得又一重大成就.實現月球背面軟著陸需要解決的一個關鍵技術問題是地面與探測器的通訊聯系.為解決這個問題，我國發射了嫦娥四號中繼星“鵲橋”，鵲橋沿著圍繞地月拉格朗日L2點的軌道運行.L2點是平衡點，位于地月連線的延長線上.設地球質量為M1，月球質量為M2，地月距離為R，L2點到月球的距離為r.根據牛頓運動定律和萬有引力定律，r 滿足方程：=（R+r）.設α=，由于α 的值很小，在近似計算中≈3α3，則r 的近似值為（ ）.

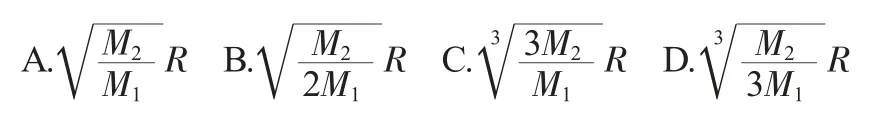
點評：本題主要考查了考生的閱讀理解能力、數式變形能力以及運算求解能力.

二、突出考查重點知識，考查考生的理性思維能力和邏輯推理能力

2019 年高考數學全國卷注重對高中數學基礎知識的考查，突出考查主干知識，注重素養導向，考查考生的理性思維能力和邏輯推理能力.

例2 （2019年高考全國Ⅲ卷文理科第15題）如圖1，設F1，F2為橢圓C：=1 的兩個焦點，M 為C 上一點且在第一象限.若△MF1F2為等腰三角形，則M 的坐標為___________.

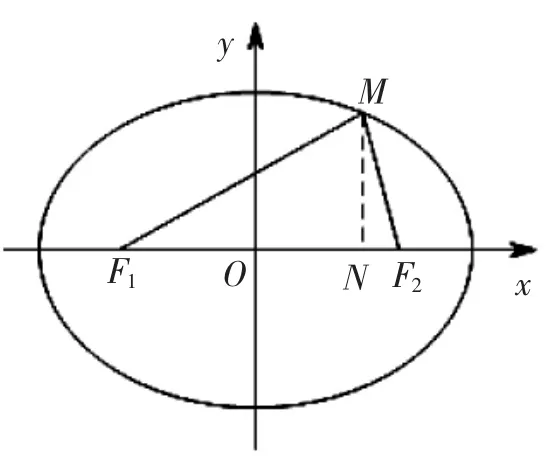
圖1

解析：由橢圓的方程可知a=6.∴c=4.∵△MF1F2是等腰三角形，且F1F2=8，，∴△MF1F2是以F1為頂點的等腰三角形.設M（m，n）（m＞0，n＞0）.∵MF1=F1F2，∴（m+4）2+n2=64①.∵點M（m，n）在橢圓上，∴=1②.由①②解得答案應填（3，）.

點評：本題主要考查了數形結合思想、轉化與化歸思想，很好地落實了直觀想象、邏輯推理等數學核心素養.

三、聯系生活實際，考查考生運用數學知識分析和解決實際問題的能力

2019 年高考數學全國卷對實際應用問題的考查有所加強，注重創設日常生活、生產實踐、科學探究等問題情境，考查考生運用數學知識分析和解決實際問題的能力.

例3 （2019年高考全國Ⅲ卷理科第16題）學生到工廠參加勞動實踐，利用3D 打印技術制作模型.如圖2，該模型為長方體ABCD-A1B1C1D1挖去四棱錐O-EFGH 后所得的幾何體，其中O 為長方體的中心，E，F，G，H 分別為所在棱的中點，AB=BC=6cm，AA1=4cm，3D 打印所用原料的密度為0.9g/cm3，不考慮打印損耗，制作該模型所需原料的質量為___________g.

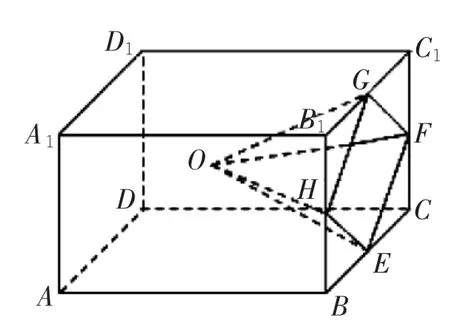
圖2

解析：由題意可知SEFGH=4×6-4××2×3=12cm2，四棱錐O-EFGH 的高3cm.∴VO-EFGH=×12×3=12cm3.又∵長方體ABCD-A1B1C1D1的體積V長方體=4×6×6=144cm3，∴該模型的體積V=V長方體-VO-EFGH=144-12=132cm2，其質量為0.9×132=118.8g.

點評：本題將物理知識融入數學知識中，主要考查了空間幾何體的體積問題，解題的關鍵是根據幾何體的體積與質量的關系理解題中的信息，利用相關的公式正確地求出質量.

四、注重學科知識之間的相互融合，考查考生對數據的整理及求解能力

2019 年的高考數學全國卷注重社會大課堂的引領作用，引導學生走出學科、走向社會，用學科知識解決生活中的真實問題，將物理、化學等知識與數學知識相聯系，體現了學科知識之間的相互融合.

例4 （2019年高考全國Ⅲ卷理科第17題）為了解甲、乙兩種離子在小鼠體內的殘留程度，進行如下試驗：將200 只小鼠隨機分成A，B 兩組，每組100 只，其中A 組小鼠給服甲離子溶液，B 組小鼠給服乙離子溶液.每只小鼠給服的溶液體積相同、摩爾濃度相同.經過一段時間后用某種科學方法測算出殘留在小鼠體內的離子的百分比.根據試驗數據分別得到如下直方圖（圖3）：

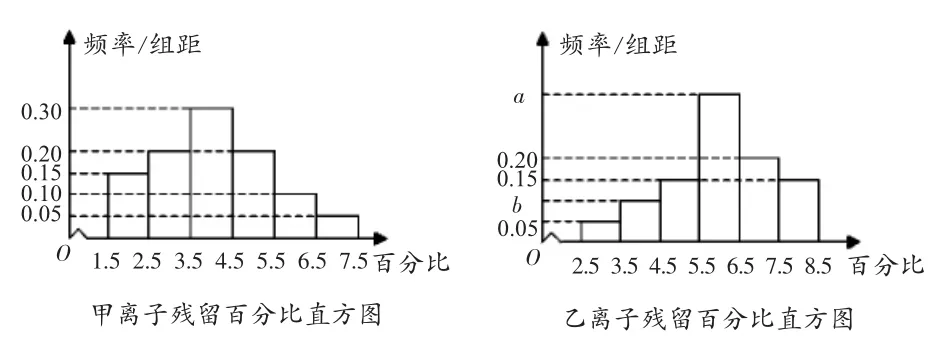
圖3

記C 為事件：“乙離子殘留在體內的百分比不低于5.5”，根據直方圖得到P（C）的估計值為0.70.

（1）求乙離子殘留百分比直方圖中a，b 的值；

（2）分別估計甲、乙離子殘留百分比的平均值（同一組中的數據用該組區間的中點值為代表）.

解析：

（1）由題意，得a+0.20+0.15=0.70.解得a=0.35.由0.05+b+0.15=1-P（C）=1-0.70，解得b=0.10.

（2）由上述離子殘留百分比直方圖可知，甲離子殘留百分比的平均值為0.15×2+0.20×3+0.30×4+0.20×5+0.10×6+0.05×7=4.05，乙離子殘留百分比的平均值為0.05×3+0.10×4+0.15×5+0.35×6+0.20×7+0.15×8=6.

點評：本題將化學知識與數學知識相聯系，體現了學科之間的相互融合，主要考查了頻率分布直方圖、平均數等知識，著重考查了考生對數據的整理及求解能力.