對2019年全國高考新課標Ⅲ卷數學第18題的探究

漾濞縣第一中學 秦慶雄 范花妹 張 鐘

2019 年全國高考新課標Ⅲ卷數學第18 題是一道中等難度的試題.通過對本題的進一步探討，教師不僅可以強化學生對數學基礎知識的理解和掌握，而且可以發展學生的思維能力，提高學生的數學核心素養.

例題（2019年全國高考新課標Ⅲ卷第18題）：△ABC 的內角A，B，C 的對邊分別為a，b，c，已知=bsinA.

（1）求B；

（2）若△ABC 是銳角三角形，且c=1，求△ABC 面積的取值范圍.

一、解法賞析

解析：

（2）這一問的解法較多，這里提供以下三種，以供讀者參考.

評注：解法1借助正弦定理，把三角形的面積這個目標函數轉化為角的形式，然后再借助函數的性質來解決，推理嚴謹、踏實可靠，是解決這類問題的通性通法，但運算量較大，對學生的運算能力要求較高.

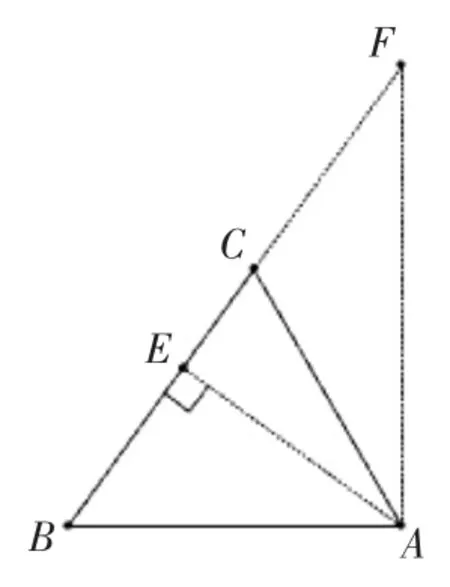
解法2（幾何法）：由題設及（1）可知，△ABC 的邊c=1 為定長，角B=為定值，由此可以構造出右圖，滿足△ABC 是銳角三角形的點C 在線段EF 上（端點除外）.當點C 在E 處時，.又∵c=1，∴.∴S△ABC=.當點C 在F 處時.又∵c=1，∴b=.∴S△ABC=.∵點C 在線段EF 上（端點除外），∴△ABC 面積的取值范圍是.

評注：解法2結合問題特征，構造出幾何圖形來求△ABC面積的取值范圍，直觀迅速，但對數形結合、幾何知識和邏輯推理等方面有一定的要求.

評注：解法3將動態問題進行靜態化處理，運算量小且準確率高，但過程不夠嚴謹，只能用于猜測或驗證所求答案的正確性.極限法別有洞天，是解答選擇題和填空題的最佳解法，常給人一種舉重若輕的神奇效果.

解題不反思，無異于“進寶山而空返”.問題解決后，我們切不可萬事大吉，真正的功夫還在于解題之后.解完題后，教師還要善于引導學生總結解題的策略和方法，使之成為今后的一種解題模式.

二、推廣探究

將第（2）問中已知的角和邊都一般化，可以得到結論1：

結論1：在銳角△ABC 中，已知∠B 和c，則△ABC 面積的取值范圍是（）.

將結論1 中的c 換成b，可以得到結論2：

結論2：在銳角△ABC 中，已知∠B 和b，則△ABC 面積的取值范圍是（].（讀者可自行嘗試證明）

三、教學啟示

解三角形一直有“無難題”之說，但從今年的試題來看，這類試題有加大難度的趨勢，應該引起教師和學生的注意.解法1 思路比較自然，學生只要掌握課本上的基礎知識和考試說明中要求的基本思想方法就能順利求解此題，并不需要什么特殊技巧.然而，還是有相當一部分學生在解答此題時暴露出基礎知識薄弱、解題目標意識不強、轉化意識淡薄、公式運用僵化、運算能力欠佳等問題.在解答此題的過程中，數學的基礎知識、基本思想方法、基本技能、基本活動經驗的重要性再一次得到詮釋，通性通法的意識和掌握程度必須提高.具體說來，我們在今后的教學中應注意以下幾個問題.

1.夯實基礎、回歸教材.

在新課教學中，教師要注重基礎知識、基本概念的形成過程，加強過程教學，讓學生主動參與到新知識、新概念的建構過程中來，盡可能讓學生親自探索、發現新知.在解題過程中，教師要養成“回到基本概念中去”的解題習慣，從而引領學生夯實基礎，熟練運用課本知識解決“基礎題”.在復習階段，回歸教材既是“以不變應萬變”的復習策略，又是提高備考效率的有效途徑.教師要站在系統與結構的寬度、思想與方法的深度、聯系與區別的高度去把握課本中的概念、定義、定理、公式、例題、習題等，通過延伸拓展、變式訓練等策略有效地提高復習的效率.

2.立足通性通法.

在平時復習時，教師要堅持“題不在多，理解則靈”的理念，要重視對各章節知識中通性通法的復習和掌握，要切實淡化特殊技巧.重視通性通法的教學，不僅能不斷地將學生的思維引向數學的基本概念和基本思想，使學生養成良好的思考習慣，而且能讓學生以“不變”的思考方法應對“萬變”的數學題目.只有這樣，我們才能擺脫題海，達到事半功倍的效果.

3.培養學生的數學運算能力.

對于解法1，大部分學生都望而卻步，其主要原因是數學運算不過關.因此，在平時的教學中，教師應注重對學生數學運算能力的培養.數學運算主要表現為：理解運算對象、掌握運算法則、探究運算思路、求得運算結果等，通過數學運算促進數學思維能力的發展，學生可以形成規范化思考問題的習慣.

4.培養學生的轉化意識和綜合運用知識的能力.

在解題教學中，教師要善于引導學生真正參與到思維活動中來，讓學生學習如何讀題、分析題意，如何進行多元聯系、多角度轉化，如何研究已知與未知的關系，獲得解題思路，如何實施并適時調整解題策略等.每解完一題，教師都要引導學生學會總結和反思，力求讓學生對數學概念和解題規律的理解有所加深，在轉化的意識和方法上有所加強，以期達到做一題、連一片、熟一類的教學效果，讓學生在解題中學會解題，從而真正提高課堂教學的效率.這樣定能為學生謀取更長遠的利益，真正發揮數學教學的育人功能，同時也可以提升教師自身的數學素養.