液壓軸向柱塞泵容積效率可靠性靈敏度分析

杜尊令, 張義民, 王悅勇

(沈陽工業大學 機械工程學院, 沈陽 110870)

高壓、高轉速條件下, 柱塞泵的油液泄漏是造成柱塞泵容積效率降低的主要原因，而各運動副之間的間隙是造成油液泄露的重要因素之一[1-3]. 由于制造公差、流體的粘度系數和體積壓縮系數、溫度、外部載荷等工作條件影響，軸向柱塞泵各運動副間隙具有隨機性，特別是軸向柱塞泵運行時所處的工況的不同，難以用確定性模型完成柱塞泵容積效率的相關分析，因此對柱塞泵容積效率的可靠性分析變得十分重要.

國內外對柱塞泵泄漏的研究多集中在泄漏量求解及實際流量脈動分析. 文獻[2,4]通過對軸向柱塞泵三大運動副間隙的泄漏和摩擦損失進行分析，建立了新的物理尺寸模型. 文獻[1,5]假設各運動副之間間隙是傾斜的，提出了一種新的軸向柱塞泵泄漏和實際流量波動模型. 文獻[6]討論了現有柱塞泵流量損失模型與實測數據對比，分析不同模型的優缺點. 文獻[7]考慮了柱塞腔中油液的可壓縮性及通過各個間隙的向外泄漏問題，應用數值積分法求解實際流量. 上述方法在間隙泄漏分析中認為參數是確定的，而實際柱塞泵運行中大部分因素是隨機和不確定的.

可靠性是指產品在規定的使用條件下、規定的時間內完成規定功能的能力[8-10]. 將可靠性技術與液壓相結合，產生了液壓可靠性這一方向. 目前對液壓柱塞泵可靠性研究較少，文獻[11]提出了液壓柱塞泵關鍵元件抗磨損和抗疲勞的可靠性設計和可靠性靈敏度分析方法. 文獻[12]對柱塞進行動力學分析，并結合應力—強度干涉模型對柱塞進行抗疲勞可靠性分析. 針對柱塞泵可靠性的研究主要集中在磨損和疲勞等方向，對于柱塞泵間隙泄漏引起容積效率的可靠性分析很少涉及. 本文對柱塞泵各運動副間隙瞬時泄漏流量進行了全面分析，推導出柱塞泵瞬時泄漏流量和容積效率計算方法，結合可靠性理論，四階矩技術和隨機攝動理論提出柱塞泵容積效率可靠性分析方法. 采用Monte Carlo方法驗證了文中所提方法的準確性和合理性，通過可靠性靈敏度分析得到各設計參數對柱塞泵可靠性的影響程度. 本文所提方法為軸向柱塞泵研發設計、工藝、質量等人員在研發、制造、檢驗等環節提供理論參考.

1 單柱塞瞬時流量及泄漏流量

1.1 單柱塞瞬時流量

軸向柱塞泵主要由滑靴-斜盤副、柱塞-缸體副、缸體-配流盤副三對主要運動副組成(如圖1所示). 柱塞組在缸體旋轉作用下作回轉運動，在斜盤作用下沿軸線方向作直線往復運動，通過配流盤的作用，將油液從吸油腔中吸入，從排油腔排出，其單個柱塞理論瞬時排油量qpv為

qpv=Apvp=ApωRptanγsinφ=

(1)

式中：vp為柱塞相對柱塞腔的運動速度，dp為柱塞直徑，ω為缸體轉動角速度，Rp為柱塞分布圓半徑，γ為斜盤傾斜角，φ為缸體轉角.

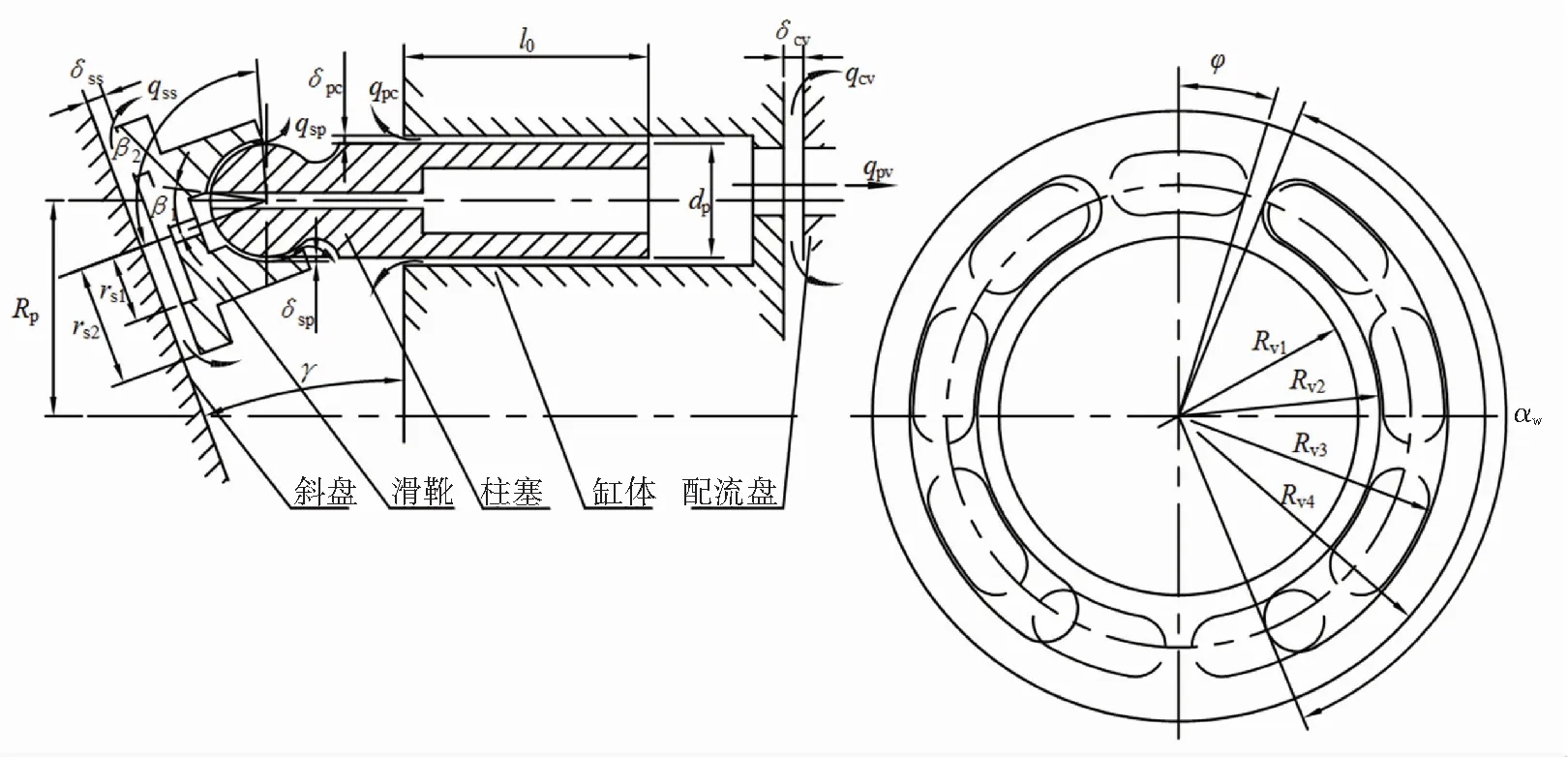
圖1 軸向柱塞泵間隙泄漏示意圖Fig.1 Main clearance leakage flows of the axial piston pump

1.2 單柱塞瞬時泄漏流量

軸向柱塞泵各運動副之間要形成適當的油膜，以減少運動過程中摩擦副之間的摩擦磨損及其造成的功率損失，運動副之間形成的油膜間隙，勢必造成一定的泄漏流量，從而降低容積效率[13]. 本文除上述三對運動副之外，還分析了滑靴與柱塞球鉸接之間的間隙泄漏量. 由于各運動副之間的間隙值是隨缸體的轉動周期變化的，間隙值一般在0.05～0.25 mm之間，在此假設它們是層流.

1.2.1 滑靴與斜盤之間間隙的瞬時泄漏量

滑靴在旋轉過程中，在離心力作用下產生傾覆與斜盤產生傾斜角，其間隙隨著缸體轉角的變化而發生周期性的波動，位于排油區時，其傾斜角和間隙相對較小，位于吸油區時，其傾斜角和間隙較大；當缸體轉速增加時，間隙增大，當排油壓力增大時，其間隙變小[14]. 當柱塞-滑靴組位于排油區時，高壓油通過柱塞中心孔流入滑靴中心孔，滑靴中心孔高壓pd和滑靴外回油壓力p0產生壓差，通過滑靴與斜盤之間的油膜間隙產生泄漏[15]. 其單個滑靴瞬時泄漏量qss為

(2)

式中：δss為滑靴與斜盤之間的間隙，μ為油液的動力粘度，rs2為滑靴底面外圓半徑，rs1為滑靴底面內圓半徑.

1.2.2 滑靴與柱塞球鉸接之間間隙的瞬時泄漏量

球鉸接可以繞一個中心點完成兩個方向轉動，具有高負載能力、高抗沖擊能力和自動調心能力而常被用于軸向柱塞泵[5]. 柱塞泵中滑靴與柱塞通過球鉸運動副鉸接在一起，其單個球鉸副間隙泄漏量qsp為

(3)

式中：δsp為滑靴與柱塞球鉸接之間間隙，β1和β2分別為柱塞和滑靴球頭有效作用角度.

1.2.3 柱塞與缸體柱塞腔之間間隙的瞬時泄漏量

柱塞在缸體轉動過程中會在柱塞孔內周期性地微運動，在離心力和斜盤傾斜力的作用下，其中心線與柱塞腔中心線發生偏心和傾斜；傾斜角和偏心量隨缸體轉角的變化而波動，隨缸體轉速的增加，偏心量減小，泄漏量也相應減小[16-17]. 柱塞與缸體柱塞腔之間的間隙泄漏量由柱塞兩端壓力差造成的壓差泄漏和柱塞往復運動造成的剪切泄漏流量兩部分組成. 其泄流量qpc為

(4)

式中：δpc為柱塞與柱塞腔同心時的單邊間隙，l0為柱塞在上止點時柱塞與缸體的接觸長度，ε為相對偏心量. 式中“±”號前半部分為縫隙壓差形成的泄漏，后半部分為純剪切流動的泄漏，壓差方向與運動方向一致時取“+”號，反之取“-”號.

1.2.4 缸體與配流盤之間間隙泄漏量

缸體與配流盤之間間隙隨排油區壓力的變化而波動，位于排油區間隙較小，吸油區間隙較大，在一個循環周期內其間隙為楔形并時刻發生著改變；伴隨負載壓力的升高，排油區間隙變小，吸油區間隙變大，即楔形角變大[18]. 在排油區時排油腰槽內高壓與卸油口之間形成壓差，通過缸體與配流盤之間的間隙，產生泄漏量qcv為[7]

(5)

式中：αw為配流盤腰型槽包角，δcv為缸體與配流盤之間間隙，Rv1、Rv2為配流盤內封油帶的內外半徑，Rv3、Rv4為配流盤外封油帶的內外半徑.

2 軸向柱塞泵瞬時流量及泄漏量分析

2.1 軸向柱塞泵瞬時流量分析

柱塞泵共有z個柱塞，這些柱塞在缸體中沿圓周方向均勻分布，任一相鄰兩柱塞夾角為2π/z，設同時處于排油區內柱塞的個數為m，若z為偶數，同時位于排油區和吸油區分布的柱塞數均為m=z/2；若z為奇數時，其同時位于排油區柱塞數m為

(6)

其同時位于吸油區柱塞個數為z-m. 柱塞泵的瞬時流量Qpv為

(7)

通過推導計算，柱塞泵的瞬時理論流量Qpv為

(8)

2.2 軸向柱塞泵瞬時泄漏量分析

2.2.1 柱塞泵柱塞-缸體副剪切泄漏量分析

假設柱塞泵中有n個柱塞與腔體之間存在間隙剪切泄漏，其n個柱塞的瞬時剪切流Qc為

(9)

柱塞泵的柱塞與柱塞腔之間的間隙剪切泄漏不僅存在于排油區，當柱塞位于吸油區時依然存在，因此z個柱塞全部存在剪切泄漏，將m=z帶入式(9)得Qc=0，即柱塞泵中柱塞與柱塞腔中產生的間隙瞬時剪切泄漏量為零，與柱塞個數為奇數或偶數無關. 考慮單個柱塞泄漏分析時間隙剪切泄漏是有意義的，對于整個柱塞泵泄漏分析，其柱塞與缸體間隙瞬時剪切總泄漏流量為零，因此柱塞泵的瞬時泄漏只考慮壓差泄漏.

2.2.2 柱塞泵泄漏量分析

柱塞泵的瞬時泄漏量為任一時刻柱塞泵中滑靴-斜盤副、滑靴-柱塞副、柱塞-缸體副和缸體-配流盤副的間隙泄漏量之和，各運動副之間的間隙泄漏主要是由于壓差引起，柱塞位于吸油區壓力差值相對較小，本文僅考慮柱塞位于排油區時的泄漏問題. 其瞬時總泄漏流量QL為

(10)

當柱塞數z為偶數時

(11)

當柱塞數z為奇數時

(12)

式中“±”號的取值按照式(6)選取.

從式(11)～(12)可以看出液壓柱塞泵的間隙泄漏量主要與各間隙值、柱塞泵幾何尺寸、排油區壓力和油液運動粘度有關.

3 容積效率可靠性及可靠性靈敏度設計

3.1 柱塞泵容積效率

容積效率是衡量液壓泵性能的一個重要指標，液壓泵的油液泄漏是造成其容積效率降低的主要原因. 通過運動副之間間隙泄漏模型分析，其容積效率ηv為實際輸出流量與其理論流量之比，即

(13)

3.2 可靠性設計

根據應力-強度干涉模型，軸向柱塞泵容積效率極限狀態方程和可靠度R分別表示為

g(X)=ηv-[ηv]≥0,

(14)

R=P[g(X)≥0].

(15)

式中[ηv]為容許容積效率，由JB/T7043- 2006《軸向柱塞泵》[19]可知在額定工況下，公稱排量10≤V<25 mL/r時，軸向柱塞泵容許容積效率[ηv]≥91%.

二階矩法是在已知基本隨機參數的前兩階矩，可靠性指標定義為

(16)

在基本隨機參數矩陣X服從正態分布時，可以獲得可靠度的估計量:

RSM=Φ(βSM),

(17)

如果已知基本隨機參數的前四階矩，可靠性指標定義為

(18)

式中:α3g=θg/σg3為狀態函數g(X)的偏態系數，α4g=ηg/σg4為狀態函數g(X)的峰態系數.

四階矩的可靠度為

RFM=Φ(βFM).

(19)

3.3 可靠性靈敏度設計

機械零部件基于四階矩技術的可靠度對隨機參數向量X均值和方差的靈敏度為

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

4 數值算例

4.1 柱塞泵容積效率

為驗證本文所提方法的準確性，以某柱塞泵為例進行仿真分析，其仿真參數為：dp= 0.016 7 m，Rp=0.030 65 m，P0=0 Pa，Pd=21×106Pa，γ=17.5°，μ=0.028 Pa·s，ω=157 rad/s，rs1=0.008 5 m，rs2=0.012 m，β1=0.261 7 rad，β2=2.006 rad，l0= 0.041 m，αw=2.686 4 rad，Rv1=0.024 4 m，Rv2= 0.029 6 m，Rv3=0.034 4 m，Rv4=0.036 7 m.

圖2和圖3分別為柱塞數為8和9時，在不同負載壓力和不同轉速下容積效率隨瞬時轉角變化的規律. 從圖中可以看出隨著壓力的增大，其泄漏量增加，容積效率下降；隨著轉速的升高，泵的流量增加，容積效率上升.

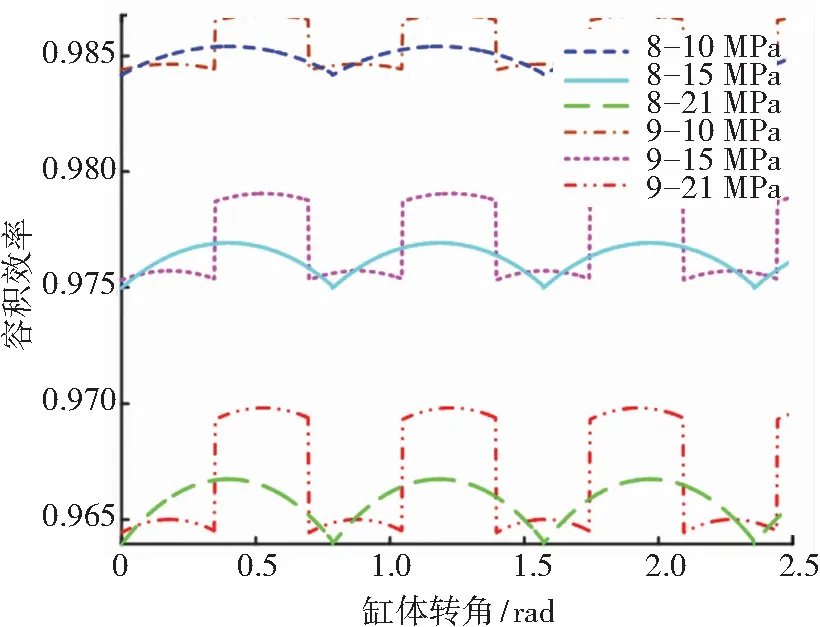
圖2 不同壓力下容積效率變化曲線Fig.2 Volumetric efficiency variation curve under different pressures

圖3 不同轉速下容積效率變化曲線

Fig.3 Volumetric efficiency variation curve under rotating speeds

4.2 容積效率可靠性及可靠性靈敏度分析

液壓柱塞泵各運動副在運動過程中，其間隙的高度值隨缸體旋轉角度而瞬時變化的，且在不同工況下具有隨機性；在設計過程中選取X=[δssδspδpcδcv[ηv]]T為設計變量，其參數見表1.

表1 柱塞泵的相關參數Tab.1 Relative parameters of the piston pump

Monte Carlo方法又稱為計算機隨機模擬法，是通過對隨機變量反復的大量抽樣，或產生隨機數樣本，對抽樣結果進行統計分析，獲得系統響應的統計規律. Monte Carlo方法在可靠性分析中具有通用性強、精度高等特點，但由于采用大量反復的抽樣，工作量較大，在實際工程中很難應用，現階段Monte Carlo方法通常作為標準驗證其他方法準確性和有效性[20-22].

分別取柱塞數z為8和9時，利用Monte Carlo方法抽樣108次和文中所提方法進行計算結果對比，得到的可靠度曲線如圖4和圖5所示.

圖4 柱塞個數為8時的可靠度變化曲線

Fig.4 Reliability variation curve when the number of pistons is 8

圖5 柱塞個數為9時的可靠度變化曲線

Fig.5 Reliability variation curve when the number of pistons is 9

由圖可知兩種算法計算結果十分接近，驗證了文中所提方法的準確性. 基于容積效率的液壓軸向柱塞泵可靠度隨著缸體旋轉角度呈周期性變化，當柱塞通過斜盤上止點時其可靠度最低. 柱塞個數為8時其可靠度曲線波動相對較小，以缸體轉角2π/8為周期變化；柱塞個數為9時其可靠度曲線波動相對較大，以缸體轉角2π/9為周期變化，并當柱塞轉角通過π/9時發生較大波動，但其整體可靠度水平高于柱塞個數為8時.

圖6和圖7為柱塞個數分別為8和9時的參數在均值點處無量綱化之后的靈敏度. 從圖中可以看出其整體變化趨勢趨近于其可靠度變化趨勢，各設計參數相對于可靠度負相關，即參數值越大，其可靠度越低. 容許容積效率對可靠性影響最大，其次是滑靴與斜盤之間間隙δss和缸體與配流盤之間間隙δcv， 柱塞與柱塞腔之間間隙δpc和滑靴與柱塞球鉸接副之間間隙δsp對柱塞泵可靠度影響較小.

圖6 柱塞個數為8時的均值靈敏度變化曲線

Fig.6 Mean sensitivity variation curve when the number of pistons is 8

圖8和圖9為柱塞個數分別為8和9時的參數無量綱化方差靈敏度. 從圖中可以看出其整體變化趨勢趨近于無量綱化均值靈敏度，各設計參數方差值相對于可靠度負相關，即方差值越大，其可靠度越低. 容許容積效率方差值對可靠性影響最大，其次是滑靴與斜盤之間間隙δss和缸體與配流盤之間間隙δcv， 柱塞與柱塞腔之間間隙δpc和滑靴與柱塞球鉸接副之間間隙δsp影響較小.

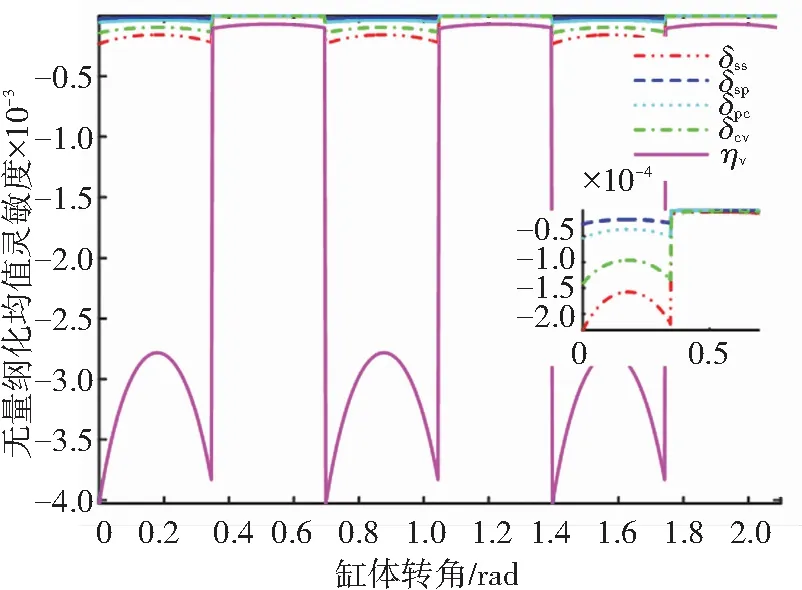
圖7 柱塞個數為9時的均值靈敏度變化曲線

Fig.7 Mean sensitivity variation curve when the number of pistons is 9

圖8 柱塞個數為8時的方差靈敏度變化曲線

Fig.8 Variance sensitivity variation curve when the number of pistons is 8

圖9 柱塞個數為9時的方差靈敏度變化曲線

Fig.9 Variance sensitivity variation curve when the number of pistons is 9

5 結 論

1)建立了基于容積效率的液壓軸向柱塞泵四階矩可靠性模型，并用Monte Carlo方法驗證了該方法的準確性和合理性.

2)對柱塞個數為8和9時進行分析，柱塞通過上止點位置時其可靠度最低，柱塞個數為9時其可靠度波動較大，但其整體可靠性水平優于8個柱塞.

3)利用四階矩理論建立了軸向柱塞泵可靠性靈敏度分析模型，通過各運動副間隙值和容許容積效率作為設計參數，對柱塞泵可靠度的影響程度進行分析.

4)各運動副間隙值對可靠性影響程度中，滑靴與斜盤和缸體與配流盤之間間隙對可靠度影響較大，柱塞與柱塞腔和滑靴與柱塞球鉸接副之間間隙對可靠度影響較小.