玻纖/環氧樹脂復合材料非線性粘彈性響應

孫同生, 于存貴, 楊文超,2, 仲健林

(1.南京理工大學 機械工程學院, 南京 210094； 2.江西長江化工有限責任公司, 江西 九江 332006)

纖維增強聚合物基復合材料因具有比強度高、比剛度高和可設計性好等優點而被廣泛地應用于先進輕質結構中，如航空航天飛行器、火箭發動機殼體、火箭武器定向器等[1-3]. 這些結構的設計服役壽命通常是幾年甚至十幾年，因此在結構設計時需要考慮材料的長期力學性能. 大多數聚合物在載荷和環境因素作用下表現出時間相關的粘彈性響應，使得粘彈性成為聚合物基復合材料長期力學性能的重要組成部分.

國內外學者基于力學元件組合模型和時間-溫度等效原理對聚合物及其復合材料的線性粘彈性開展了大量研究工作[4-7]. 然而，研究表明：聚合物基復合材料的線性粘彈性存在應力閾值，即當應力超過一定值或在高溫、高濕度環境下會表現出明顯的非線性特征[8]. 因此，研究人員提出很多理論模型來描述材料的非線性粘彈性響應，主要包括多重積分理論和單積分理論. 多重積分理論，如G-R理論[9]，盡管能夠準確地描述材料的非線性粘彈性，但是需要通過一系列復雜的試驗來獲得繁多的材料參數，很難應用到實際工程問題. Bernstein等[10]在G-R理論的基礎上提出了預測應力松弛行為的非線性粘彈性本構方程(BKZ模型). 王禮立等[11]通過對多種材料進行試驗研究，提出了一種適用于中低應變率(10-4～103)的非線性唯象本構模型(ZWT模型). 該模型與其他非線性粘彈性模型有本質區別，其非線性體現在非線彈性響應，而模型中的粘彈性部分則是線性的. Schapery[12]基于不可逆熱動力學理論，提出了一種含折算時間的非線性粘彈性本構關系. 該模型表征的材料的非線性粘彈性響應由4個與應力、溫度和吸濕量有關的參數來控制. Schapery模型較為簡單，并且可通過選擇不同的線性粘彈性模型，如冪率模型[13]和廣義Kelvin模型[14]，來獲得多種不同形式的非線性本構模型，在聚合物以及聚合物基復合材料中得到了廣泛應用. 應用Schapery模型的關鍵是通過一系列不同應力水平的短期(0.5～8 Hrs)蠕變-回復試驗獲得非線性參數隨應力的變化規律，通常采用數值擬合法[8]和基于等效性原理的圖形移位法[15]辨識非線性參數，存在效率低、人為主觀因素對結果影響較大的缺點.

復合材料的粘彈性主要受聚合物基體控制，通常認為連續纖維增強聚合物基復合材料在纖維方向上不具有粘彈性，而在橫向和面內剪切方向上具有明顯的粘彈性[16]. 因此，本文針對玻纖/環氧復合材料，分別在橫向和面內剪切方向上開展不同應力水平的短期(1 Hrs)拉伸蠕變-回復試驗，根據試驗得到的典型蠕變-回復應變曲線提出一種基于解析法的非線性參數辨識方法，獲得非線性參數隨應力的變化規律，研究玻纖/環氧復合材料的非線性粘彈性響應.

1 理論模型

1.1 Schapery非線性本構關系

等溫條件下單軸載荷作用時，Schapery單積分型非線性粘彈性本構關系為

(1)

式中:ψ和ψ′稱為折算時間

(2)

(3)

D0為初始柔量，與時間無關，表征材料的瞬時彈性響應；非線性參數g0，g1，g2和aσ均與應力有關，且受環境溫度和材料吸濕量影響[17]. 當g0=g1=g2=aσ=1時，式(1)退化為線性粘彈性本構.ΔD(ψ)為時間相關的瞬態線性蠕變柔量，表征材料的蠕變響應，通常采用冪率模型來表示:

ΔD(ψ)=Dψn，

(4)

式中D、n與環境溫度和材料吸濕量有關，與應力水平無關.

1.2 非線性參數辨識方法

對于蠕變-回復試驗，施加圖1所示的應力歷史，得到的典型非線性蠕變-回復應變時間曲線如圖1所示. 可以看出，聚合物基復合材料在經過一段時間的回復過程后，會存在一定的殘余粘塑性應變. 因此，將粘塑性應變分量引入Schapery非線性本構關系，得到

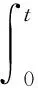
(5)

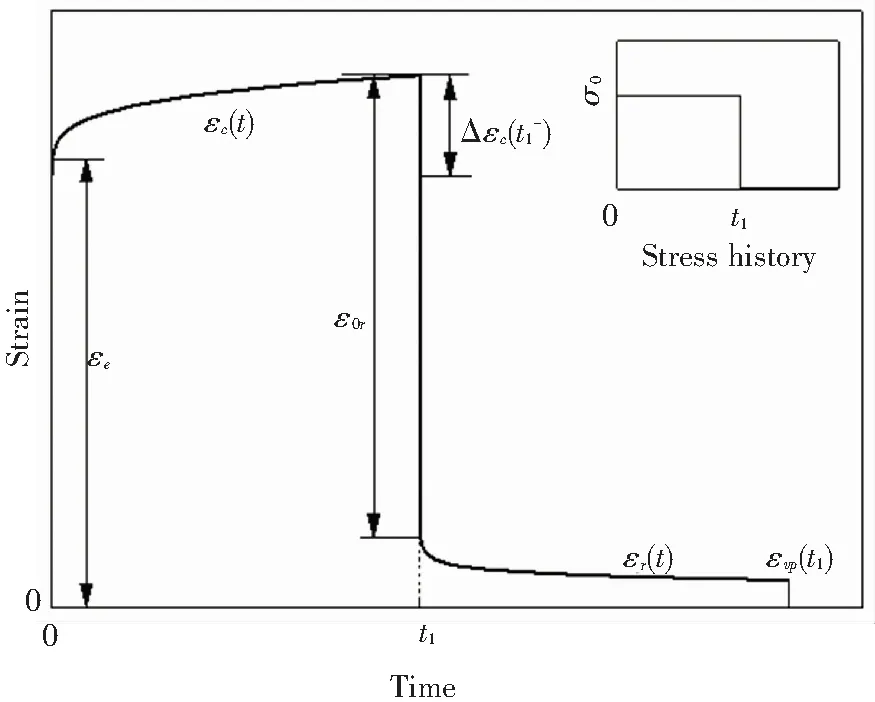
圖1 蠕變-回復試驗應變時間曲線

Fig.1 Typical strain-time curve for creep-recovery test

將式(4)由冪律模型表示的瞬時蠕變柔量代入式(5)中，得到材料的蠕變、回復應變分別為

(6)

(7)

式中λ=(t-t1)/t稱為無量綱時間，Δε1=g1g2D(t/aσ)nσ0為蠕變應變.

1.2.1 非線性參數g0和g1

非線性參數g0表示不同應力水平下初始彈性柔量偏離線性響應的程度，可通過將不同應力水平的初始彈性柔量與最低應力水平對應的初始彈性柔量對比獲得.

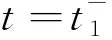
(8)

(9)

(10)

結合式(9)和式(10)可以得到卸載瞬間的應變變化量為

(11)

由此得到加載與卸載瞬間的應變差值為

(12)

求解式(12)得到非線性參數g1的解析解如下:

(13)

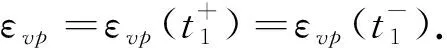
對于線性蠕變-回復響應，g1=1，則εvp=0，即線性情況下不存在殘余粘塑性應變，這與試驗觀察到的現象一致.

1.2.2 非線性參數aσ和g2

非線性參數aσ表示時間移位因子，反映了高應力水平對復合材料蠕變行為的加速效應. 式(7)中Δε1和εvp(t1)可以直接從蠕變-回復應變曲線上獲得，因此若已知時間指數n的值，則非線性參數aσ可利用式(5)對由試驗得到的回復應變數據做單一參數擬合得到.

非線性參數g2反映了加載速率對粘彈性響應的影響程度. 在已知非線性參數g1，aσ和n的前提下，可以得到非線性參數g2的解析解.

由式(12)得到

(14)

(15)

式中：Δε0(nl)表示非線性情況下加載與卸載瞬的瞬時應變差值；Δεc(l)表示線性情況下保載t1時長后的蠕變應變量；σ0(nl)和σ0(l)分別表示非線性與線性情況下施加的應力值，本文選擇最低應力水平作為σ0(l).

2 試驗材料與方法

2.1 試驗材料及成型工藝

由于目前沒有可依據的蠕變試驗標準，參照復合材料基本力學性能測試標準GB/T3354-2014[18]和GB/T3355-2014[19]制備復合材料蠕變試樣. 試樣原材料為G20000型單向玻璃纖維預浸料，名義厚度為0.17 mm，單位面積質量為200 g/m2，纖維體積含量約為67%，由威海光威復材有限公司提供. 試樣采用模壓成型工藝制備，鋪層方式為[90]16和[±45]4S，厚度約為2 mm. 固化工藝：120 ℃，2 MPa條件下保溫2 h，保壓冷卻至室溫后脫模.

2.2 試驗方法

蠕變試驗前，先進行準靜態拉伸試驗測試單向板的基本力學性能，為合理選擇蠕變試驗的應力水平提供依據. 蠕變試驗中加載的應力水平應在極限強度的10%～80%之間，若應力水平過高，試樣容易出現蠕變斷裂，應力水平過低，則短期內不會出現明顯的蠕變變形[20]. 準靜態試驗采用2 mm/min的加載速度，測試得到單向板基本力學性能參數如表1所示，表中數據為5個試樣的平均值.

表1 單向板彈性性能Tab.1 Elastic properties of GFRP unidirectional plates

在室溫環境下，采用1 h蠕變/1 h回復的方式開展拉伸蠕變-回復試驗，其中，橫向上共包括7個應力水平，分別為橫向拉伸強度的35%、41%、47%、53%、60%、66%和72%；面內剪切方向上共包括8個應力水平，分別為剪切強度的19%、25%、31%、37%、43%、49%、56%和62%. 由于受到試驗機力傳感器的限制，加載時采用最大允許加載速度250 N/s來加載，所有試樣均在15 s之內完成加載，與蠕變-回復時間相比，加載時間足夠短，可以近似認為是瞬時加載. 準靜態試驗與蠕變-回復試驗均在三思縱橫UTM5105-G型電子萬能材料試驗機上進行. 利用漢中精測BF120-3AA型電阻應變計、江蘇聯能YE3818C型動態應變儀、YE29003A型橋盒和美國NI9215型數據采集器測量記錄試樣的應變值. 為排除試樣吸濕對復合材料粘彈性的影響，在粘貼應變片之前利用南京沃環WH101-2A(S)型電熱鼓風干燥箱將試樣烘干72 h至恒重，烘干溫度為50 ℃. 此外，試驗過程中接入溫度補償片，排除環境溫度變化造成的應變測試誤差.

3 結果分析

3.1 蠕變-回復應變時間曲線

試驗得到不同應力水平的蠕變-回復應變時間曲線如圖2所示. 可以看出，玻璃纖維增強環氧樹脂復合材料在基體性能主導的材料方向上表現出明顯的粘彈性行為，并且隨著應力水平的升高，呈現出一定的非線性. 此外，觀察試驗結束時刻的應變值，可以發現在低應力水平下，殘余粘塑性應變非常接近零線，而隨著應力的增大，殘余粘塑性應變明顯增大，這在一定程度上說明了提出的參數辨識方法的合理性. 不同時間點試樣的等時應變曲線如圖3所示. 可以看出，當施加的橫向拉伸應力超過26 MPa，面內剪切應力超過15 MPa時，試樣的應變偏離線性行為，表現出明顯的非線性粘彈性.

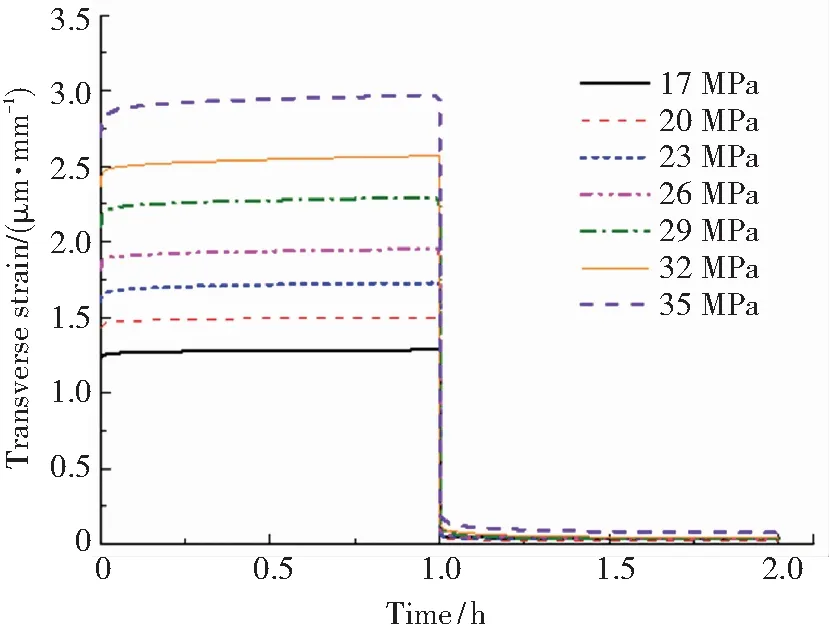
(a) [90]16橫向試樣

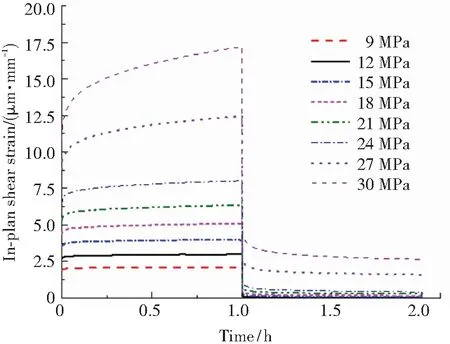
(b) [±45]4S面內剪切試樣圖2 GFRP在不同應力水平下的蠕變-回復應變曲線

Fig.2 The 1 h creep and 1 h recovery strain curves of GFRP corresponding to different stress levels

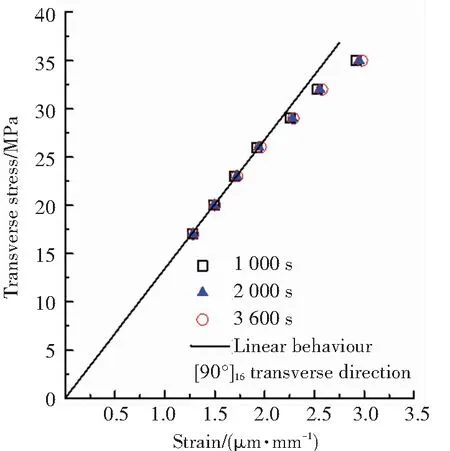
(a) [90]16橫向試樣

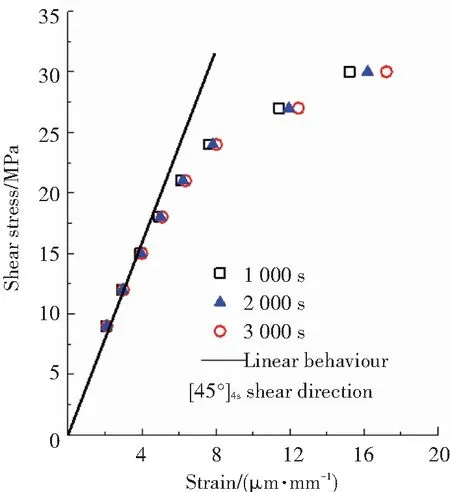
(b) [±45]4S面內剪切試樣圖3 不同時間點的等時應力-應變曲線Fig.3 Isochronous stress strain curves at different time periods

3.2 非線性參數變化規律

3.2.1 非線性參數g0

根據不同應力水平加載結束時刻的應力應變計算得到初始彈性柔量，并分別與低應力水平對應的初始彈性柔量對比，得到非線性參數g0隨應力的變化規律如圖4所示. 橫向上，參數g0T基本不隨應力發生變化，說明玻纖/環氧樹脂復合材料的橫向彈性柔量與應力無關；面內剪切方向上，當施加的剪應力大于15 MPa時，參數g0S隨應力呈指數增加. 根據初始彈性柔量計算得到橫向彈性模量為13.7 GPa，面內剪切模量為4.42 GPa，與表1中通過準靜態拉伸試驗得到的彈性模量有一定區別，這主要是由于加載方式和加載速度不同引起的，說明聚合物基復合材料為率相關材料.

3.2.2 非線性參數g1

根據式(13)計算得到不同應力水平下非線性參數g1如圖5所示. 可以看出，兩個材料方向上，當應力大于非線性應力閾值時，非線性參數g1T和g1S均隨應力線性增加，表明隨著應力的增加，復合材料的非線性粘彈性程度逐漸增加.

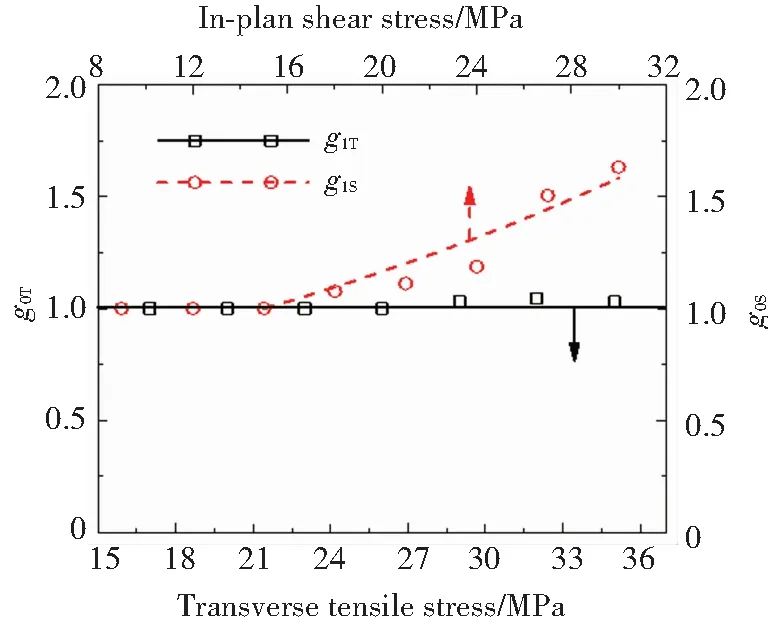
圖4 非線性參數g0隨應力的變化規律Fig.4 Nonlinear parameter g0 as a function of applied stress

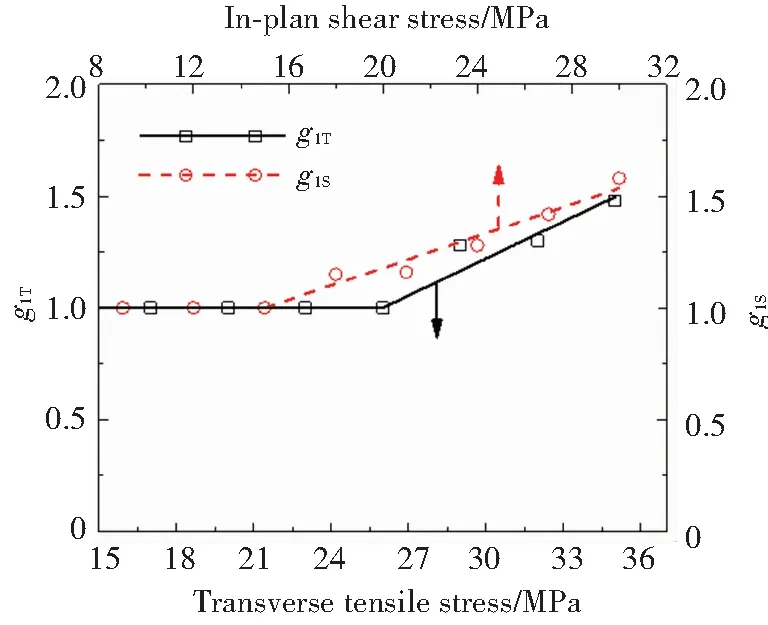
圖5 非線性參數g1隨應力的變化規律Fig.5 Nonlinear parameter g1 as a function of applied stress

3.2.3 非線性參數aσ

在獲得非線性參數aσ之前，首先需要獲取冪率模型的時間指數n的值. 研究表明，在恒溫恒濕度環境中，時間指數n與應力水平無關. 并且，n與蠕變的時間尺度有關，而與回復的時間尺度無關[8]. 因此，首先利用式(7)對線性粘彈性范圍內(此時，g0=g1=g2=aσ=1)的回復應變曲線進行擬合，得到橫向上時間指數n的平均值為0.080，面內剪切方向上時間指數n的平均值為0.044. 在此基礎上，采用Levenberg Marquardt迭代算法，利用式(7)擬合非線性回復應變曲線，得到aσ隨應力的變化規律如圖6所示. 可以看出，在非線性范圍內，兩個材料方向上的非線性參數aσ均小于1，并且隨應力線性降低，這說明高應力水平下短時間的粘彈性響應與低應力水平下長時間的粘彈性響應相對應，即高應力水平對玻纖/環氧復合材料的粘彈性起到了加速作用.

3.2.4 非線性參數g2

由于參數g1，aσ和n已知，利用式(15)采用解析法直接求得參數g2，如圖7所示. 橫向上，非線性參數g2T基本不隨應力發生變化，g2S在非線性范圍內則隨應力呈指數增加. 需要特別注意的是，按照本文提出的參數辨識方法，非線性參數aσ和g2的準確性主要依賴于g1，因此要在原始試驗數據中準確判斷各關鍵節點，如蠕變起點、終止點和回復起點等.

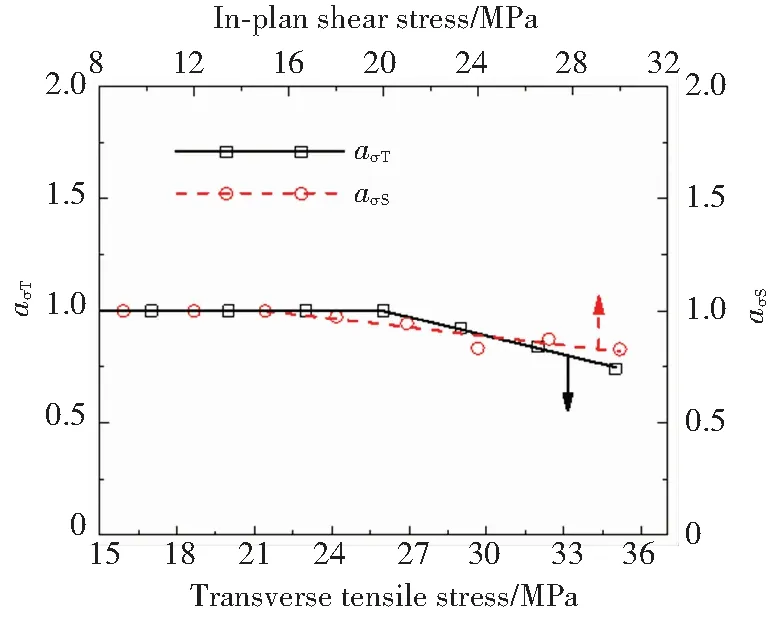
圖6 非線性參數aσ隨應力的變化規律Fig.6 Nonlinear parameter aσ as a function of applied stress

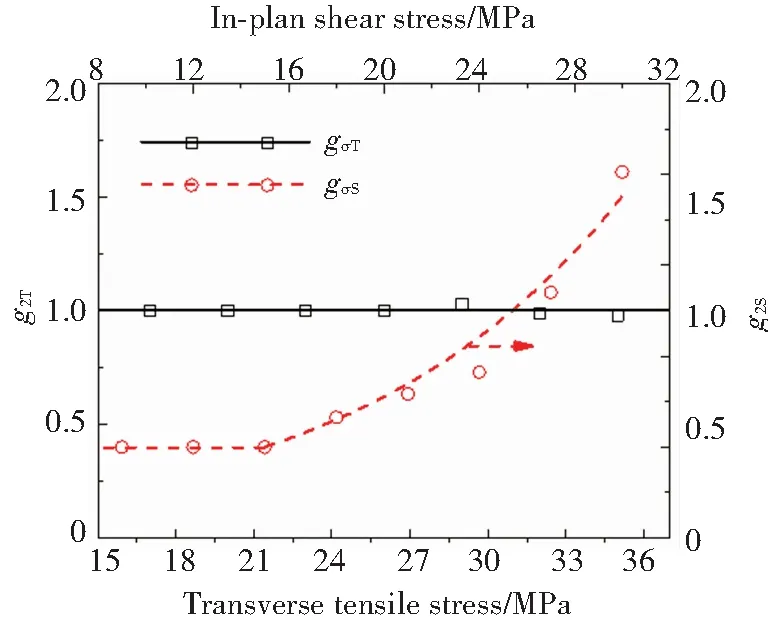
圖7 非線性參數g2隨應力的變化規律

Fig.7 Nonlinear parameterg2as a function of applied stress

4 結 論

1)通過在Schapery非線性本構關系中引入殘余粘塑性應變分量，提出一種基于解析法的非線性參數辨識方法，只需要依據原始試驗數據確定蠕變起點、終點和回復起點的應變值，便能快速獲取非線性參數隨應力的變化規律.

2)當施加的橫向拉伸應力大于26 MPa(橫向拉伸強度的53%)，面內剪切應力大于15 MPa(剪切強度的31%)時，玻纖/環氧復合材料表現出明顯的非線性粘彈性響應.

3)在橫向上，非線性參數g0T和g2T與應力無關，g1T隨應力線性增加，而aσT則隨應力線性降低.

4)在面內剪切方向上，非線性參數g0S和g2S隨應力呈指數增加，g1S隨應力線性增加，而aσS則隨應力線性降低.