分階式四點接觸齒輪的滾刀齒面設計

2020-06-24 02:48:56高艷娥汪久根

哈爾濱工業大學學報 2020年7期

高艷娥, 張靖, 汪久根

(1. 浙江大學機械工程學院，杭州，310058；2. 西南大學工程技術學院，重慶；400715；3.浙江雙環傳動機械股份有限公司，浙江臺州，317600)

齒輪是極其重要的核心基礎件，影響齒輪傳動性能的主要因素有嚙合齒面、潤滑狀態、表面粗糙度、材料及熱處理方式等，其中嚙合齒面作為運動和動力變換的直接作用面，對齒輪的性能具有非常重要的影響，因此如何獲得具有良好幾何特性和接觸特性的嚙合齒面是提高齒輪性能的關鍵問題[1-3]. 國內外學者對嚙合齒面進行了深入研究，主要方法有齒面修形和構建新的嚙合齒面[4-7].

齒面修形主要有三維拓撲修形、齒形修形和齒向修形，國內外很多學者在該領域進行了大量的研究，如方宗德等對人字齒輪的主動輪進行三維修形[8]，設計了對角修形斜齒輪齒面[9]，建立了面齒輪修形簡化模型[10-11]，研究了鼓形修形對載荷分布的影響[12]；彭先龍等[13]提出了齒面主動修形方法來預控斜齒面齒輪的嚙合性能并消除邊界接觸；張西金等[14]提出了圓弧齒廓刀具修形及齒向鼓形修形的方案；Pedrero等[3]研究了修形對嚙合剛度、載荷分布和傳動誤差的影響. 目前，關于齒輪嚙合理論的研究仍然以共軛曲面原理為基礎，對常用齒輪傳動齒形的優化、修正、構型仍然是研究的重點，這些研究對提高齒輪傳動的性能起到了積極作用，但是仍然未從根本上解決問題.

在構建新的嚙合齒面方面，陳揚枝等[15-16]建立了空間曲線沿接觸點主法線方向的嚙合方程及嚙合曲線方程，獲得了具有直徑的鉤桿曲齒傳動；陳兵奎等[17]提出了曲線共軛嚙合理論，將給定運動兩構件上的光滑曲線始終保持相切接觸定義為曲線嚙合，給出了由共軛曲線形成嚙合齒面的一般方法，并將該理論應用于平行軸和相交軸齒輪傳動[18-21]. 由于共軛曲線的接觸具有靈活性和多樣性，既可以在節圓內嚙合，又可以在節圓上嚙合，還可以在節圓外嚙合；齒輪在運動的過程中可以有多對共軛曲線同時參與嚙合，共軛曲線對數目增加，同時接觸的點的數目相應增加，接觸區域擴大，可以減少跑合時間，增加齒輪的承載能力；多對曲線同時參與嚙合時，共軛曲線對的分布對齒輪的傳動性能有顯著影響. 前期的研究中，設計的共軛曲線凸齒齒輪在節圓外嚙合，凹齒齒輪在節圓內嚙合，在加工時需要設計兩把刀具，如果齒輪能在節圓內和節圓外同時實現多對共軛曲線接觸，且在加工時僅需一把刀具即可加工出相互嚙合的一對齒輪，不僅可以顯著降低制造成本，而且能大幅度提高齒輪傳動的性能.

本文在共軛曲線嚙合理論的基礎上，提出分階式多點接觸齒輪，并以分階式四點接觸齒輪為例，開展齒輪的基本齒形設計，進而推導滾刀的齒面方程，求解齒面方程并建立滾刀的精確實體模型，根據實體模型，獲得滾刀實體，完成分階式四點接觸齒輪副的滾切試制.

1 分階式多點接觸齒輪

所謂分階式多點接觸齒輪，是指齒輪的嚙合齒面分為上嚙合齒面和下嚙合齒面，呈階梯分布，由過渡齒面連接. 齒輪副運動時，小齒輪的上嚙合面與大齒輪的下嚙合面嚙合，有兩個或兩個以上的接觸點，小齒輪的下嚙合面與大齒輪的上嚙合面嚙合，有兩個或兩個以上的接觸點，上下嚙合齒面同時在四個接觸點接觸. 齒輪在嚙合時，多對共軛曲線同時參與嚙合，工作齒面在多個接觸點同時接觸. 以分階式四點接觸齒輪為例，如圖 1所示，齒輪嚙合齒面上有4條共軛曲線，在嚙合時，上嚙合面有兩個接觸點，下嚙合面有兩個接觸點.

分階式四點接觸齒輪副在運動時，如圖 2所示，小齒輪上嚙合齒面與大齒輪下嚙合齒面嚙合，小齒輪下嚙合面和大齒輪上嚙合面嚙合，均為凹凸接觸，加載之后，接觸位置由于彈性變形從接觸點擴展為接觸面，承載能力提高，具有接觸強度高、重合度高的特點. 齒輪嚙合時，接觸點僅在齒寬方向移動，無齒高方向移動，相對于漸開線齒輪，傳動比較平穩，滑動率很低，摩擦損失少，傳動效率高.

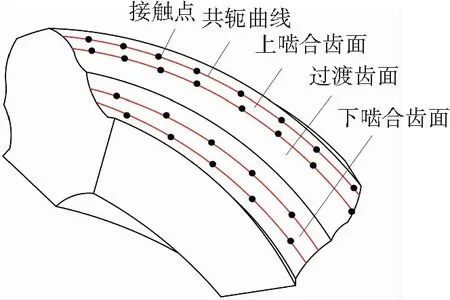
圖1 分階式多點接觸共軛曲線齒輪Fig.1 Multi-point contact gear with ladder shape of teeth

圖2 單齒嚙合Fig.2 Single tooth meshing

2 分階式四點接觸齒輪的基本齒形

嚙合齒面是由刀具基本齒形通過展成運動得到的，因此基本齒形對嚙合齒面的傳動性能具有重要影響. 取刀具的法面齒廓為基本齒形，同側齒面的基本齒形有兩段工作齒廓，分別有兩個接觸點，在嚙合時共有4個接觸點，如圖 3所示，圖中α1、α2為接觸點處的壓力角.

圖3 基本齒形嚙合Fig.3 Basic tooth profile meshing

刀具的法面齒廓如圖 4所示. 切削刃I是半徑為ρ的圓弧，將切削出上嚙合齒面;切削刃II是半徑為rf的圓弧，將切削出過渡齒面; 切削刃Ⅲ為拋物線，將切削出下嚙合齒面; 切削刃IV是半徑為rj的圓弧，將切削出齒根過渡曲面.ha和hf分別為齒頂高和齒根高;h為全齒高.Sa為凸齒齒廓部分齒厚; Sf為凹齒齒廓部分齒厚.δ1為工藝角. 建立坐標系Sn(On;xn,yn,zn)與齒條固連，xnOnyn平面與齒條法面重合，坐標軸xn與齒廓的對稱軸線重合，yn與齒條節線重合.

圖4 刀具法面齒廓Fig.4 Normal tooth profile of rack cutter

根據齒條的幾何形狀，可得各切削刃在坐標系Sn中的方程為

(1)

式中：α為自變量參數，ρ為圓弧的半徑，(0,la) 為圓弧圓心在坐標系xnOnyn中的坐標值.

(2)

式中：αj為自變量參數，rj為圓弧的半徑，(ej,lj)為圓弧圓心在坐標系xnOnyn中的坐標值.

τmin≤τ≤τmax.

(3)

式中：τ為自變量參數;σ為設計參數,σ=0.5(α1+α2),α1和α2為法面壓力角；p為拋物線參數,p=ρcos (σ/2);L1=0.5ρtanσsinσ+ρcosσ.

(4)

式中:αf為自變量參數；rf為圓弧半徑，(ef,lf)為圓弧圓心在坐標系xnOnyn的坐標值.

3 滾刀的齒面方程

3.1 坐標系與坐標變換

如圖 5，分別建立固定坐標系S0(O0-x0,y0,z0)和活動坐標系S1(O1-x1,y1,z1) 與滾刀固連. 坐標軸z0和z1重合，為滾刀的旋轉軸線. 活動坐標系Sp(Op-xp,yp,zp) 與齒條固連. 坐標軸zp與zn的夾角為β.u為坐標原點Op和On在zn軸上的距離.

圖5 展成過程 Fig.5 Gear generating

在整個展成過程中，齒條刀具的節面和滾刀的節圓柱始終保持相切接觸. 滾刀繞回轉軸線z1逆時針旋轉，旋轉角速度為ω1，同時齒條刀具將向左平移，速度為vp. 當齒輪繞軸線旋轉一個角度φ1，齒條刀具將向左平移r1φ1.

根據坐標變換理論，坐標系Sn與Sp之間的坐標變換矩陣為

坐標系Sp與S0之間的坐標變換矩陣為

(6)

式中:r1為齒輪的節圓半徑；Mpn為坐標系Sn到Sp的變換矩陣，M0p為坐標系Sp到S的變換矩陣.

3.2 嚙合方程

設點M為嚙合點，根據式(1)～(5)可以獲得點M在坐標系Sp中的表達式為

(7)

式中:當i=I時，t=α；當i=Ⅱ時，t=αj；當i=Ⅲ時，t=τ；當i=IV時，t=αf.

嚙合點M的法線可以在坐標系Sp表示為

(8)

嚙合點M的相對速度在坐標系Sp中表示為

(9)

式中：vp為嚙合點隨刀具齒條的移動速度，vp=-r1ω1jp;v為嚙合點隨齒輪的運動速度，v=-ω1×r1;ω1=-ω1kp;r1=(r1+xp(u,t))ip+(-r1φ1+yp(u,t))jp+zp(u,t)kp.

根據齒輪嚙合原理，任意嚙合點處的公法線與相對速度方向垂直，其嚙合方程可以在坐標系Sp中表示為

(10)

將方程(8) 和(9) 代入方程(10)，可得

(11)

式(11)確定了齒條的移動距離參數u和滾刀的轉角φ1以及切削刃參數t的關系.

3.3 齒面方程

根據齒輪嚙合原理，滾刀齒面可以用方程表示為

(12)

將式(6),(7)和(11) 代入式(12), 滾刀齒面方程可以在坐標系S1中表示為

r(t,φ1)=

(i=I,II,Ⅲ,IV) .

(13)

式中：當i=I時，t=α；當i=Ⅱ時，t=αj；當i=Ⅲ時，t=τ；當i=IV時，t=αf.

式(13) 中齒面只有兩個變量，切削刃參數和滾刀的旋轉角度，當給出兩個變量的變化范圍，即可獲得所需齒面.

將切削刃式(1)～(4)代入式(13) ，即可得到各切削刃展成得到的滾刀齒面方程

(14)

(15)

r(Ⅲ)(τ,φ1)=

(16)

(17)

在式(14)～(17)中，當取上面的符號時，方程為左側齒面方程，當取下面的符號時，方程為右側齒面方程.

4 滾刀精確實體建模與試制

4.1 滾刀精確實體建模

通過給定的參數，逐一求解式(14)～(17)，即可獲得滾刀的各個齒面. 通過編程運算，求解出輪齒齒面上點的坐標，繪制圖形，并將坐標點導入三維建模軟件，建立滾刀的實體模型，如圖 6所示.

圖6 滾刀實體模型Fig.6 Model of hob

滾刀的主要參數為：法面模數為6 mm，內孔直徑為45 mm，外徑為110 mm，前角為0°，長度為140 mm，容屑槽為12個，螺旋升角為3°16′25″，頭數為1，旋向為右旋向.

根據滾刀模型，加工出的滾刀實體如圖 7所示.

4.2 滾切試制

用圖 7中的滾刀進行滾削加工，如圖 8所示，獲得的分階式四點接觸齒輪副，如圖 9所示. 齒輪副的主要參數如下：法面模數mn=6 mm，中心距a=130 mm，小齒輪齒數z1=6，大齒輪齒數z2=30，傳動比i=5，螺旋角β=33°49′19′′，齒寬B=80 mm.

圖7 滾刀實體Fig.7 Image of hob

圖8 滾齒加工Fig.8 Hobbing

圖9 分階式四點接觸齒輪副Fig.9 Four-point contact gears with ladder shape of teeth

4.3 接觸印痕檢驗

將圖9中的齒輪裝配到齒輪箱中，如圖10所示.

圖10 齒輪裝配Fig.10 Gear assembly

齒輪副裝配完成之后，將大小齒輪的輪齒表面清洗干凈，把小齒輪的輪齒表面均勻地涂上紅丹粉，旋轉小齒輪軸，檢查輪齒的接觸情況，如圖11和圖 12所示. 對于8級精度的齒輪傳動，在齒高方向上接觸線的位置偏差不超過0.25mn，在整個齒長方向上不少于工作齒長的85%. 從齒面的接觸區域可以看出，裝配后的齒輪副在齒長方向上的接觸不少于工作齒長的90%；在齒高方向上，能保證在理論的接觸線位置接觸，由于加工誤差和裝配誤差的存在，在齒高方向上有一定的位置偏差，約0.5 mm.