鏈傳動縱向動力學研究

□ 喻文廣

上海電氣集團股份有限公司 中央研究院 上海 200070

1 研究背景

在鏈傳動過程中,由于鏈輪和鏈條嚙合過程中存在多邊形效應,加之周期性沖擊載荷的作用,導致鏈傳動發生橫向、縱向振動[1-13]。其中,鏈條縱向振動將對鏈條運動的同步性與均勻性有較大影響,且對運動平穩性的影響要大于橫向振動。對于裝有縱向導軌的鏈傳動,如自動扶梯梯級鏈、步進鏈而言,橫向振動可以忽略。

對于鏈條縱向振動問題,早在20世紀90年代,國內學者就開始了相關研究,主要采用能量法對鏈傳動系統進行簡化,建立少量自由度的模型,推導出相應縱向振動方程,給出縱向振動頻率的解析解[8-11]。近十年,很多學者建立了更復雜的縱向振動模型,并應用有限單元法將鏈條離散化為若干彼此相連的縱向桿單元或者彈簧單元組合體,采用數值解法分析縱向動力學特性[12-13]。最近幾年,隨著多體動力學的發展,開始出現少量基于多體動力學理論建立鏈傳動系統復雜動力學模型的相關研究[14]。目前,在這些鏈傳動縱向振動的研究中,關于松邊鏈條對振動的影響及鏈條縱向振動模型邊界問題的研究都較少,而這些都是影響動力學分析結果的重要因素。

筆者以長節距滾子鏈為對象,建立縱向振動力學模型,研究鏈條邊界問題的處理,并考慮松邊鏈條質量對振動的影響,計算鏈條縱向振動頻率。對鏈條縱向振動開展試驗對比分析,根據試驗結果對鏈條振動模型進行參數修正,并基于修正模型分析工作段鏈條長度對振動頻率的影響。

2 動力學模型

2.1 滾子鏈一般形式

為了使研究的問題更具有一般性,建模時忽略鏈條導軌形狀、鏈條形狀和數量,以及主從動鏈輪齒數差異等因素,以鏈條運動為主要特征,將滾子鏈描述為一般結構形式,如圖1所示。圖1中,m為鏈條鏈節的等效質量,J1、J2為主從鏈輪的慣量,R1、R2為主從鏈輪的半徑。

由于鏈條全程都受導軌支撐和約束,因此鏈輪在多邊形效應作用下的縱向振動問題是影響系統性能的主要因素。

▲圖1 滾子鏈一般結構形式

2.2 縱向動力學建模

鏈條是由相同鏈節以鉸鏈形式連接起來的一種柔性體,在進行動力學建模及分析過程中,引入如下四條假設:

(1) 鏈條緊邊始終繃緊在一條直線上,附有縱向導軌約束,忽略橫向振動;

(2) 由于緊邊與松邊張力差別很大,因此僅考慮松邊質量的影響,忽略松邊剛度的影響;

(3) 將鏈條簡化為張緊的彈簧振子系統,鏈條及鏈節質量縮聚在節點上;

(4) 鏈輪是理想的無偏心輪。

依據功能原理,將主從動鏈輪轉動慣量J1、J2的等效質量分別記為m1、m2,等效到鏈條與主從動鏈輪的切點上。由于松邊兩端分別連接在主從動輪上,因此其質量與主從動輪一起參與鏈路的振動,影響系統的動力學特性。將松邊質量分別等效到主從動鏈輪上,隨同主從動鏈輪質量一起記為M1、M2,等效到鏈條與鏈輪的切點上。由于松邊鏈條由從動輪嚙入,被主動輪送出,因此將松邊質量全部計入從動輪邊。有如下關系式:

(1)

應用有限元法將鏈條離散為若干個剛度為k的彈簧振子系統組合體,將鏈節和輸運質量等效附加在節點處。對于鏈條而言,鏈輪系統是鏈條兩端的邊界,因此將主從動輪及張緊器分別沿縱向運動方向等效為兩個縱向彈簧,剛度分別記為K1,K2,作為鏈條兩端的彈性支撐邊界。

根據以上假設及等效,最終可建立鏈傳動縱向動力學模型,如圖2所示。

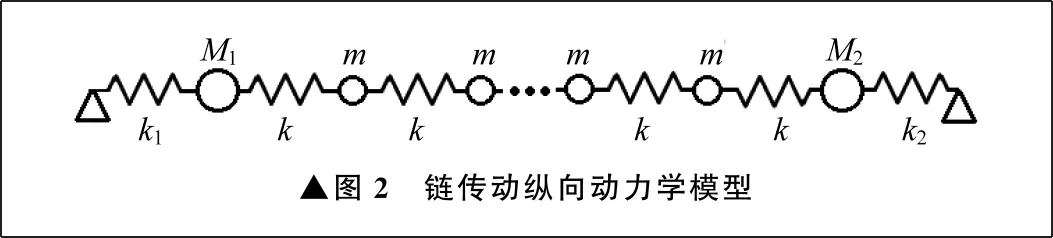
▲圖2 鏈傳動縱向動力學模型

2.3 多邊形效應

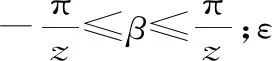
多邊形效應如圖3所示。由于多邊形效應的作用,會使鏈條速度發生周期性波動,作用在鏈條上的力也會發生周期性變化。在運動過程中,嚙合點沿縱向運動方向的速度v、加速度a及作用力F為:

v=Rωcosβ

(2)

=R(εcosβ-ω2sinβ)

(3)

F=ma

(4)

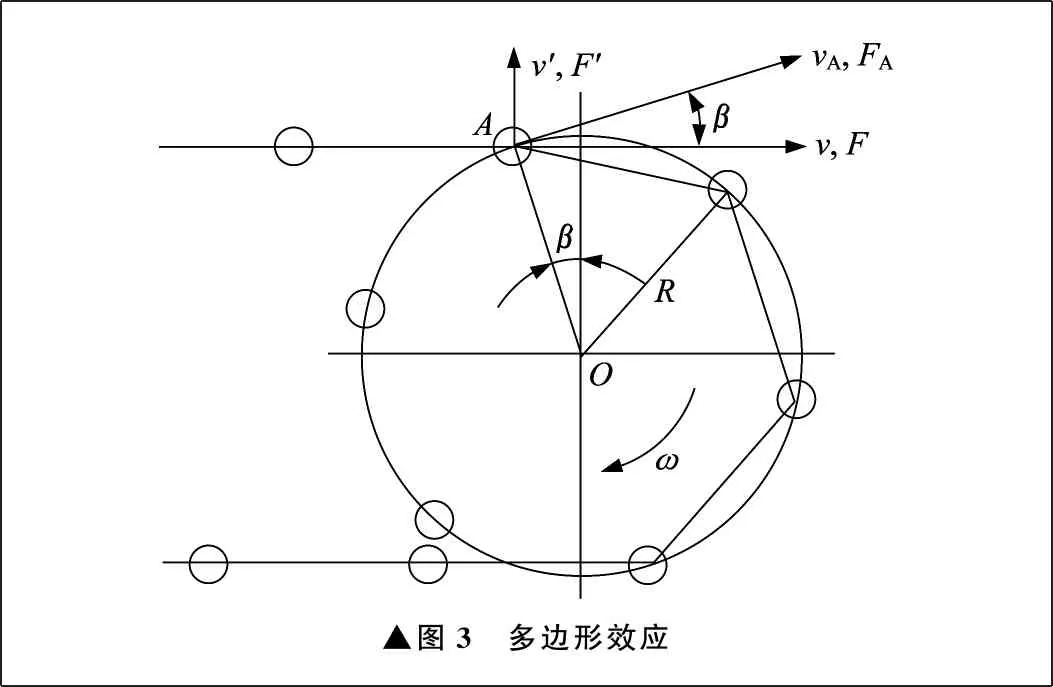
▲圖3 多邊形效應

3 動力學方程

設緊邊鏈有n個鏈節,鏈節距為l,鏈板截面積為A,鏈節質量為m,鏈條剛度為k,取鏈節點各自微小的偏離平衡位置的縱向位移u1,u2,…,un為系統的廣義坐標,將單元質量組集擴展后,得到系統的(n+1)×(n+1)階總質量矩陣M為:

(5)

同理,可以得到系統的(n+1)×(n+1)階總剛度矩陣K為:

(6)

鏈條剛度k為:

k=-EA/l

(7)

式中:E為材料的彈性模量。

系統廣義力n+1列列陣F為:

(8)

由此可得整個系統的最終總動力學方程為:

(9)

式中:U為位移矩陣。

4 分析結果

工作段鏈條長度為9 m,鏈條節距為100 mm,鏈條額定運行速度為0.6 m/s,基于上述模型,對鏈條動力學及鏈條的剛度進行計算,均采用有限元法求解和分析。

4.1 鏈條剛度及邊界剛度

鏈條在運行過程中主要承受拉伸作用,所以鏈條的剛度為拉伸剛度。對于主動鏈輪而言,除質量和轉動慣量外,對系統動力學特性影響最大的因素就是扭轉剛度。

由于鏈輪為鏈條的支撐邊界,且所建立的鏈傳動模型僅考慮縱向運動,因此將鏈輪扭轉剛度的效應等效至鏈輪鏈條嚙合點處的縱向剛度,即邊界支撐剛度k1。對于從動輪等效剛度k2,由于從動輪連接彈簧張緊器,因此計算時需要串聯張緊彈簧的剛度。

4.2 系統縱向振動頻率及響應

計算表明,鏈傳動系統的縱向振動一階頻率為6.3 Hz,二階頻率為20.7 Hz,頻率響應曲線如圖4所示。在現有鏈條運行速度下,鏈輪嚙合頻率為6 Hz,系統縱向頻率與嚙合頻率過于接近,可能導致鏈條發生縱向共振問題。

▲圖4 鏈傳動頻率響應曲線

同時對鏈傳動從啟動到平穩運行的過程進行瞬態響應分析,結果如圖5所示。隨著鏈輪運行速度的加快,多邊形效應的激勵增大,鏈節振動響應幅值也隨之增大。當運行到2 s后,振動響應幅值達到最大,此時鏈條運行速度接近額定速度0.6 m/s,對應多邊形效應的激勵頻率約為6 Hz。

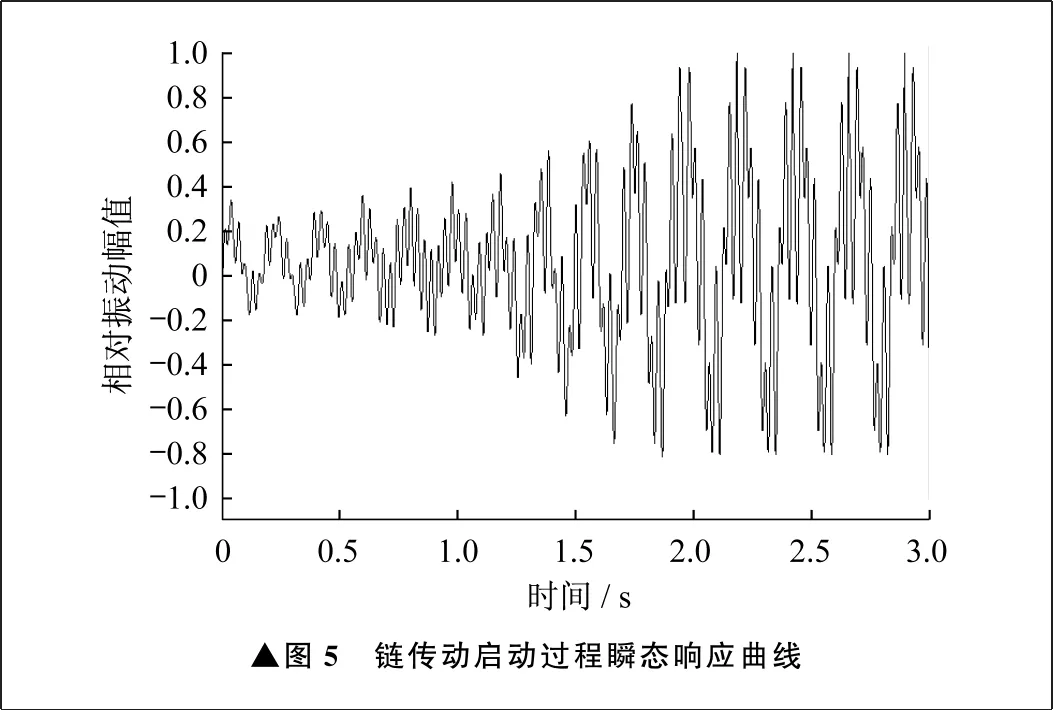
▲圖5 鏈傳動啟動過程瞬態響應曲線

5 試驗

鏈傳動動力學試驗時,將信號采集裝置固定于鏈節處,采集鏈節的振動加速度信號。為了獲取鏈條準確的縱向振動頻率,在一定范圍內對不同運行速度下的試驗結果進行分析。不同運行速度和激勵頻率下縱向振動加速度如圖6所示,可以看出隨著激勵頻率提高、運行速度加快,鏈節處縱向振動加速度幅值增大。當激勵頻率達到約6 Hz,運行速度達到約0.6 m/s,縱向振動加速度達到最大值。激勵頻率繼續提高,相對振動加速度幅值減小。所以6 Hz為鏈縱向共振頻率點,即運行速度為0.6 m/s時鏈條發生縱向共振。

畫卷內容深刻，絕不是一個方面可以涵括，一首題畫詩會有多方面的品評。 以上六類常常交錯融合，不同程度地表現在題詠上。

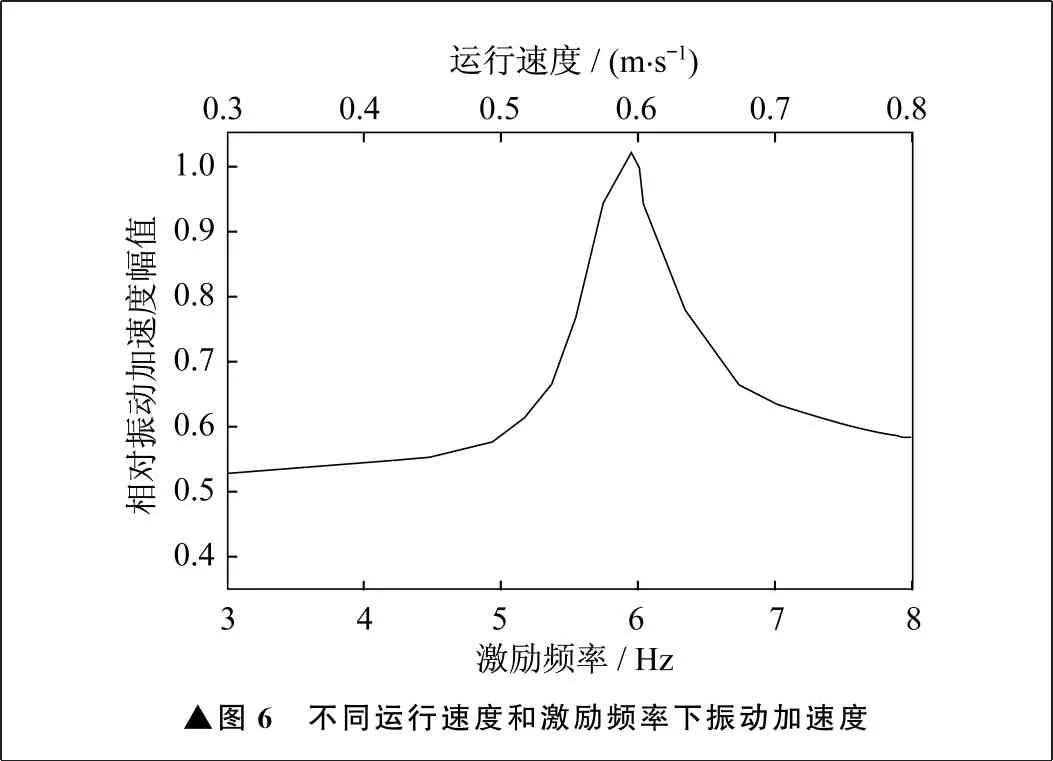
▲圖6 不同運行速度和激勵頻率下振動加速度

為了進一步研究鏈傳動的動力學特性,選取鏈條運行速度為6 m/s時的工況進行分析,對加速時域信號進行快速傅里葉變換后,獲取振動加速度響應頻域曲線。一階和二階頻率試驗與分析結果對比見表1,可見試驗結果與分析結果基本一致。

表1 頻率試驗結果與分析結果對比

系統前兩階頻率試驗結果比分析結果低,一階頻率低5%,二階頻率低10%,原因可能有兩方面。第一是在輪齒嚙合過程中,由于接觸效應存在接觸剛度,導致實際邊界剛度要比計算的剛度值低。第二是目前關于鏈輪系統等效剛度的計算及松邊質量分配并無準確分析方法,所以在等效計算過程中存在一定誤差。根據試驗結果,分別對鏈輪等效邊界剛度及松邊質量等參數進行適當修正,將修正后的模型應用于其它長度鏈條的動力學分析。

6 鏈條長度對振動的影響

基于修正后的模型,對工作段鏈條長度對鏈傳動動力學特性的影響進行分析,分別分析長度為7 m、9 m、11 m、13 m、15 m的鏈條的縱向振動頻率,結果如圖7所示。

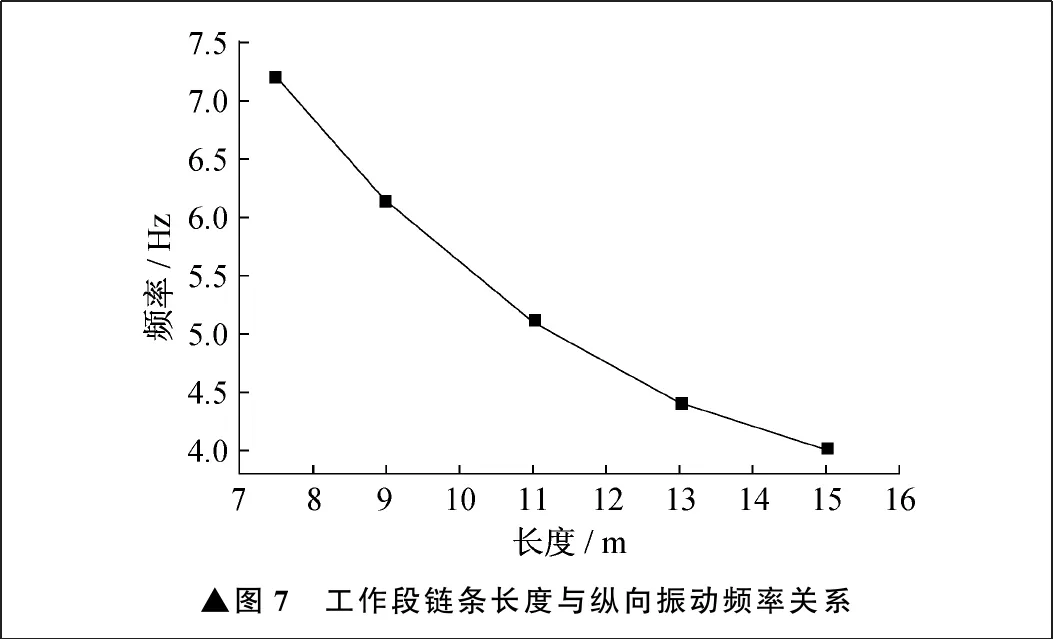
▲圖7 工作段鏈條長度與縱向振動頻率關系

由圖7可見,鏈條頻率隨著鏈條長度的增大而降低,但是降低幅度并非與長度增大成線性關系。隨著長度的增大,單位長度下頻率的降幅減小。

筆者分析的鏈傳動系統,其工作轉速一般為0.6 m/s左右,此鏈條節距下對應多邊形效應激勵頻率為6 Hz,而工作段鏈條設計長度為10 m時鏈條的結構縱向頻率為5 Hz左右,恰處于共振區間。按照結構頻率避開激勵頻率±10%的原則,當工作鏈條長度為9.25～11.75 m時,需要考慮縱向共振問題,并采取一些避振措施,如調整鏈條節距從而改變多邊形激勵頻率,或者調整鏈條剛度、質量以調整縱向頻率。

7 結束語

筆者建立了滾子鏈傳動縱向動力學分析模型,討論了鏈條邊界問題的處理,并考慮了松邊質量的影響,采用有限元方法分析了鏈傳動縱向動力學特性,進行試驗對比分析。

分析結果與試驗結果吻合良好,結果表明鏈條長度在10 m左右時會引發結構共振問題。在后續設計過程中,需要調整相關結構參數以避免共振。

鏈條模型的邊界問題是影響分析結果的重要因素,建模分析時需要考慮邊界問題的處理。

筆者建立的滾子鏈縱向動力學分析模型,對于鏈傳動問題具有一般性,可應用于其它型號滾子鏈的振動問題分析中。

鏈傳動系統是一個較為復雜的系統,筆者在建模過程中忽略了鏈輪嚙合接觸剛度等因素,對于某些問題的分析處理,如松邊質量分配、鏈輪等效剛度分析等,需要在后續研究中進一步深入完善。