借小學數學“2+1”培養，助小升初有效銜接

劉玉勇

摘 要：本文針對小學和初中數學學習的銜接問題，提出了在小學數學教學中加強學生“2+1”能力的培養。“2”就是關注方程思想的培養和重視證明方法的滲透;“1”就是培養學生錯題收集、整合和分析能力，最終達到小學向初中數學學習的平穩過渡。

關鍵詞：方程;證明;錯題;小初銜接

核心素養強調的是學生應具備的、能夠適應終身發展和社會發展需要的必備品格和關鍵能力。 核心素養對學生全面發展和可持續發展提出了要求，要求用發展的視角進行教育。因此，有序平穩地過渡不同學段的教學是每個教師所要關注的。

就教育教學現狀來看，小學和初中教學上的過渡銜接出現斷檔，是當前比較突出的問題，雖然宏觀層面有不少地區有所關注，出現了九年一貫制學校，上海等地區也采用五四學制，但外界對此各有褒貶。其實，落實化解小升初過渡問題的關鍵在人——在于教師如何整合構建二、三學段知識，精準孕伏式教學;也在于學生如何學習和消化，成為一名有知識技能儲備和學習潛力的人。作為一名小學數學教師，筆者從微觀層面，精準關注小學生數學學習中的“2+1”方面的能力滲透培養，讓學生能順利進行小升初數學學科過渡。

一、關注“2個滲透”，溝通小學和初中數學內容教學

從教學內容來看，結合小學和初中的數學課程標準，筆者認為小學階段數學教學最需要做好“2個滲透”，一個是方程思想的滲透，一個是證明方法的滲透。

（一）小學與初中數學教學內容的整體分析

從數學課程標準來看，小學和初中都安排了“數與代數”“圖形與幾何”“統計與概率”“綜合與實踐”四個領域，“2個滲透”主要數集中在前兩個領域。

“數與代數”領域中，數繼續擴充到實數;從數到式，強化代數式，從常量到變量;從算術到方程，再到方程組、不等式和函數。初中數學領域內容更具抽象性。小學在用字母表示數的基礎上，到高年級才接觸到方程，且重在初步認識和簡單運用方程;初中方程是數學最重要的內容之一，在問題解決過程中的比重比小學要大很多。

“圖形與幾何”領域中，小學重視邏輯推理，通過直觀手段尋找答案，而到了初中階段更重視抽象思維，重視數形結合，關注圖形的運動和變換，經常用先期積累的理性化的公理或定理來論證新知識。就這個領域來看，初中數學更關注對思維過程嚴密性的展示，而證明作為初中數學教學內容中最重要和最特別的內容之一，它是在探尋嚴謹思維過程的推理中產生的。

（二）關注“2個滲透”，促進小、初數學銜接

就小學和初中的數學教材對比發現，很多知識是相關的。例如，小學正反比例和初中函數相關，正負數和初中相反數相關，小學的數對知識與初中平面直角坐標系相關，小學抵消法和初中消元法相關，小學數據分析中的平均數和初中中位數、眾數、頻數、方差等相關……正是這些關聯，讓學生頭腦中的知識有了連續生長的根，學生學習過渡才顯得自然。

面對初中數學，方程思想的加強和證明方法的引入，讓很多小升初學生學習起來，存在適應和理解性困難。所以，在小學高年級數學教學中，最需要從這兩個方面加以滲透。

1.重視理解方程思想的價值。

小學數學基于用字母表示數與式子，然后在等量關系的基礎上引出方程。但就整個小學階段來看，學生接觸方程時間短，算術思維解決問題的時間長，學生更喜歡用算術方法，從已知到未知推出結論，因為在小學，很多問題用算術方法解答起來顯得更簡潔和快捷。

對于方程，它讓條件問題置于同一平臺，和使用算術方法運用的思維不同，方程更關注運用等量關系和變形，從而推算出結論。由于小學階段的教學思維結構簡單，在一般問題的解決過程中，方程體現不出思維的優勢，給學生的感覺是書寫煩瑣。同時，教師如果未強化等量關系的價值，學生更多地會將方程當成一個單一的知識或是一個問題解決的方法來學習。

其實，方程的價值是尋求一種量與量之間的平衡，可以從復雜關系中推演結論，其中蘊含了不變與變，更凝聚了很多數學思想，其建模思想對未來數學學習有著很重要的意義。而算術方法是一種單線思維，適合解決簡單關系的問題，復雜的數量關系容易造成思維的堵塞、迷茫和走偏。所以，小學階段的方程教學，更應該從價值角度進行感受。

小學生很多時候都是從直覺出發，通過解決問題來感受方程的價值。因此，小學數學教師要合理選題，從等量關系出發，讓其充分感受方程思維的獨特性和簡潔性。

例如，現有含鹽3%的鹽水240克，如果要變成含鹽4%的鹽水。需加鹽多少克？或者蒸發掉水多少克？如果用方程解答，只要抓住“加鹽”水不變，“蒸發水”鹽不變，來確定方程的等量關系，感受用方程做更利于理解的思考優勢。

2.在問題解決中嘗試證明的運用。

小學數學的思維模式更多的是從條件到問題，教學中關注從條件中收集信息，整理并推理出結論，從問題解決中整合、提煉出思維的策略或者模型。對于思維，人教版側重思維模型建立，蘇教版關注策略培養，其實都關注思維。

初中的證明，更重視學生對公理和定理的積累，讓新知在舊知基礎上不斷累積生長，并以條件和結論為兩極，讓孩子提取并使用恰當的形式、方式、策略來展示問題解決的過程，嚴謹有序地呈現從條件到問題之間的思維的有序發展。證明是小學階段鮮有發生的問題呈現形式，所以有很多學生到初中會很不適應，因此，在小學高年級可以適當運用某些題目加以形式化滲透。

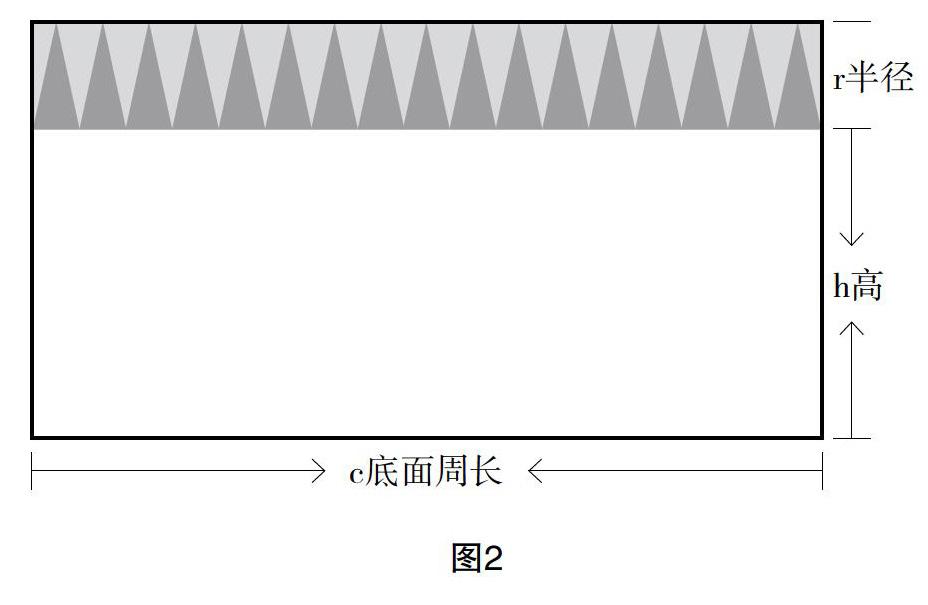
例如，完全平方是初中的內容，但小學可以用適當的形式呈現，通過面積計算和用字母表示數，通過數形結合，讓學生結合圖形，發現等量關系，對字母表達式進行運算，得出字母表達關系中量之間新的發現。（如圖1）

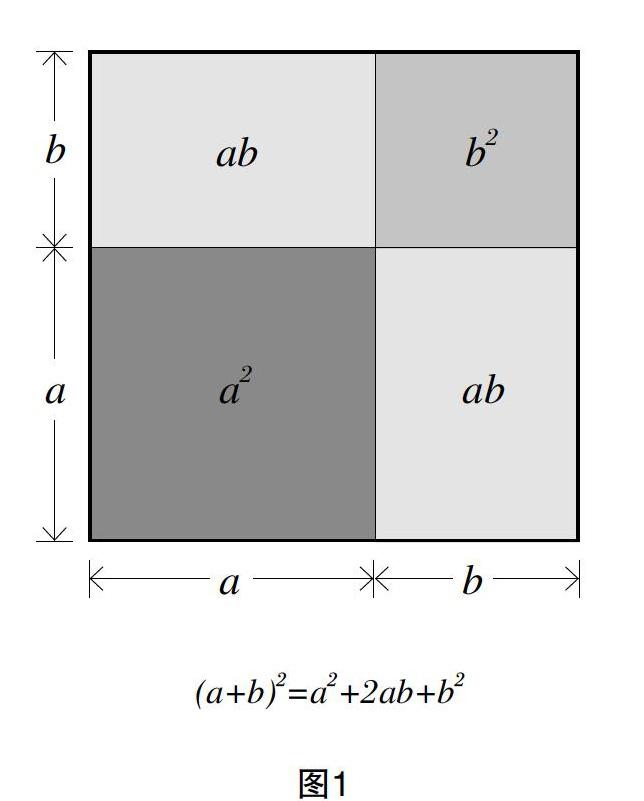
再如，除了側面加底面的算法外，圓柱表面積計算公式也有新的思考方法：S表=C×（r+h）（如圖2），對于這一等量關系，教師可以讓學生通過公式運算推導，或者通過圖形合并成長方形（寬是r+h，長C）進行說明、證明，最后可以用證明出的表面積計算方法解決實際問題。讓學生感受到證明的有趣、有意義和有價值。

小學數學中很多教學和練習內容都可以成為學生學習證明和發現新規律、新公理、新定理的沃土，小學數學教師要善于發現、運用、創造資源。

二、培養學生的“1種能力”，讓思維成長發自本體

前文從小學、初中教材和課標出發，以小學數學教師角度的改變為抓手，重點在小學數學教學中對兩點內容進行教學的滲透。

其實，學習更要關注學生主體能動性，特別是要從小學開始培養孩子錯題資源的收集和分析能力。小學數學學習，學生除了學會預習、復習和課堂記錄、練習外，也要讓學生有自我反思能力和對舊知的整合能力，因此，需要他們主動尋找最有價值的成長因子——錯題，讓錯題成為成長的催化劑。

錯題的收集有利于學生發現自己和他人的思維缺陷和困惑，也利于完整構建自己的數學知識體系和思維體系，讓學生在頭腦中編織出自己的思維導圖，讓學生的數學學習更扎實、更全面。

因此，在小學階段讓孩子逐步學會整理錯題。根據小學生的特點，錯題收集呈現形式可多樣化、趣味化，教師和家長都可以協助參與。可以讓學生將錯題循序漸進地整理在練習本上，也可以以小組為單位合并形成錯題集，還可以分組將本組的錯題組成試卷，可以文字形式，也可以圖文畫報形式呈現。作為班級學習共同中的一員，學生最后還要學會將錯題資源共享。

參考文獻：

趙培明，王亮.實現小升初數學教學有效銜接的幾點措施[J].山東教育，2016，（13）.