改進的慣性運動傳感器步態識別

徐狄濤， 姜 斌， 包建榮， 劉 超， 朱 芳， 何劍海

（1.杭州電子科技大學通信工程學院，杭州310018；2.寧波職業技術學院電子信息工程學院，浙江寧波315800）

0 引 言

隨著可穿戴物聯設備推廣，其存儲的大量私人信息面臨丟失和泄露等問題，故需采取措施來保護實驗等場所敏感信息的安全［1］。傳統識別技術（指紋識別、密碼驗證等）存在需要用戶合作、密碼遺忘、輸入錯誤的問題［2］，而步態識別技術具有更安全的數據收集程序，不需要顯式用戶的交互，以及高抗欺詐性的優點［3］，通過將傳感器集成到各種可穿戴物聯網設備中，可以輕易地提取步態信號［4］。由于Arduino 源碼開放且靈活性強［5-6］，MEMS慣性傳感器體積小且廣泛運用于電子設備［7-8］，本文以Arduino 為硬件平臺，Mpu6050 為采集模塊，藍牙為發送模塊，研發了成本低，體積小且通用性強的步態數據采集裝置，該裝置非常適用于高校實驗室步態數據的采集與分析，使基于傳感器的步態識別更具成本效益。

國外，Muaaz等［9］用動態時間規整（Dynamic Time Warping，DTW）對48 名志愿者的步態特征作匹配，得到相等錯誤率（Equal Error Rate，EER）為16.26%的性能；Derawi 等［10］采用新的交叉DTW 方法進行特征匹配，得到的準確率為89.3%。國內，何書芹等［11］采用多尺度熵和DTW結合的方法，得到EER為13.7%的效果；童偉男［12］運用多特征k 最近鄰（k-Nearest Neighbor，k-NN）分類算法，引入權值分配，使準確率達到87.6%。上述算法在一定條件下實現了步態識別，但其準確率仍不理想。為此，本文提出一種新的步態識別方法，該方法將DTW 與人工神經網絡（Artificial Neural Network，ANN）相結合，通過DTW對不同長度的步態特征參數進行規整，同時引入步長、步頻、步速特征參數，利用列文伯格-馬夸爾特（Levenberg-Marquardt，LM）優化算法改進后的BP 神經網絡［13-14］實現步態的識別，該方法在降低采樣率和網絡訓練時間的同時，有效提高了步態識別的準確率，為步態識別的研究提供了新的思路。

1 數據采集

圖1 數據采集裝置

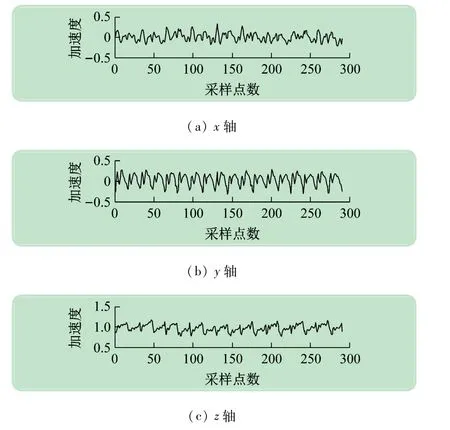
圖2 原始步態信號波形圖

本文所用的實驗平臺采用Mpu6050、Arduino開發板、藍牙模塊HC-05 構成步態數據采集裝置。Mpu6050 具有小體積、高性能、低成本、低噪聲的優點，實驗采用±2 g 的加速度計量程，在靜止狀態下，對Mpu6050 求平均消除系統誤差后，采集三軸加速度值；Arduino作為開源硬件平臺，具有便捷靈活、接口豐富、方便上手的優點，實驗采用體積小巧且功能全面的Arduino Nano 開發板，其核心處理器為ATmega328（Nano3.0），利用與硬件同名的Arduino 程序開發軟件，將編譯完的程序通過USB線傳入Arduino控制板，實現程序設計與開發；藍牙具有低功耗、低成本等優點，實驗采用HC-05 將數據采集裝置采集的數據實時傳輸到PC機，實現了數據的存儲與傳輸。實驗采集裝置如圖1 所示。

實驗采集x軸（左右方向）、y 軸（重力方向）、z 軸（前后方向）3 個軸上的加速度值，其中1 名志愿者的原始步態信號如圖2 所示。通過對比，發現重力方向的波形具有良好的周期性和穩定性。因此，本實驗選取人體重力方向的加速度信號做步態識別。

2 算法描述

2.1 特征提取

步行時支撐腿的動作包括腳跟著地、腳掌支撐、腳跟離地、初始蹬腿等［15］。這些時刻分別對應重力方向加速度信號的極值點，提取這些極值點作為特征點來進行步態識別具有明確物理意義。采用小波變換過零點方法，即通過高斯函數平滑，將其一階導數作為小波基函數，找到小波變換后的過零點，提取加速度信號極值點。本實驗提取步態周期的幅值及時間特征，并將其保存為幅值序列：M ＝［M1，M2，…，Mn］與時間序列：T ＝［T1，T2，…，Tn］。

由于步行存在偏差，即使是同一人每個周期的采樣點也不同，導致樣本的時長也不同，所以要進行時間歸一化。設每個樣本周期有n 個采樣點，將原始的加速度信號歸一化到區間［0，1］上，使樣本采樣點為整個樣本相對時間，且可歸一化為：

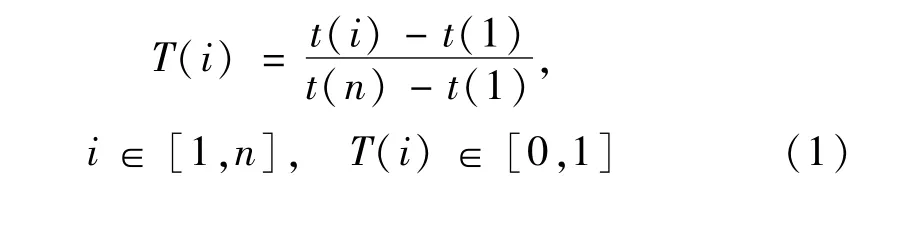
圖3 為志愿者A 和B 的步態樣本信號。從中可以清楚地發現，不同志愿者的步態曲線波動差異較大，而同一志愿者的步態則有很大相似性。特征提取后，差異更加明顯，不同志愿者在一個樣本周期內，不僅幅值大小不相同，而且相對時間也完全不同，這為步態識別提供了良好基礎。

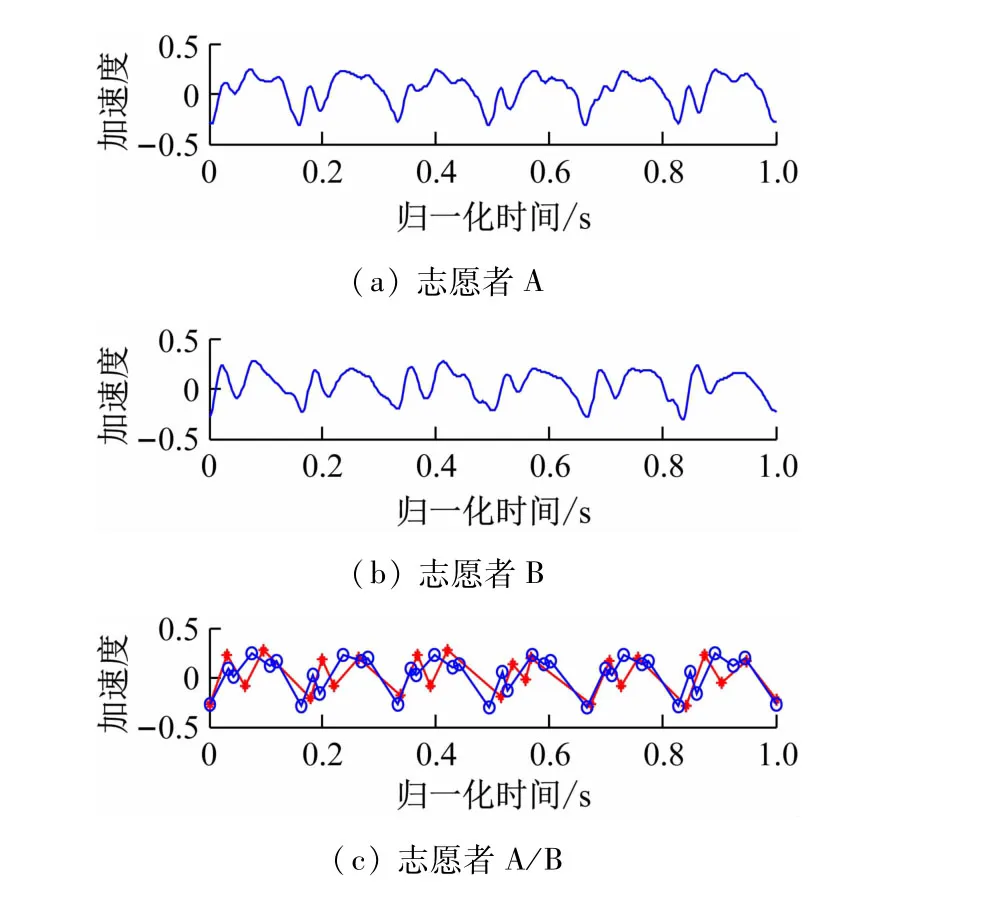
圖3 步態樣本信號及特征對比曲線圖

2.2 動態時間規整算法

因人行走時步態間存在差異，即使從同一志愿者樣本提取特征點，其個數也不同。而從不同志愿者樣本提取特征點，其個數基本都不同。因此，本實驗采用動態時間規整，通過擴展或縮短序列來計算兩個序列的相似性。

以志愿者A和B 的兩個步態周期的幅值特征序列Ma、Mb為例，設兩個特征序列分別為：MA＝［Ma1，Ma2，…，Man］，MB＝［Mb1，Mb2，…，Mbm］，為了將這兩個序列對齊，需構建一個n ×m 矩陣，矩陣中的元素（i，j）表示Mai和Mbj兩個點間的距離，即通過對彎曲函數的約束，最小累積距離的路徑有（i-1，j）、（i -1，j -1）、（i，j -1）。此時，最小累積距離可表示為

一個步態周期包括左步態和右步態共兩步。由于步態樣本長度的選取影響步態識別率，若選取樣本長度過長，則處理的數據量將大為增加；否則，提取的樣本的特征點不穩定，導致識別率降低。因此，將6 個連續步態作為一個樣本，每個樣本包含3 個完整的步態周期。設志愿者A和B的兩個參考樣本分別為：SA＝其中MAi和MBj分別表示每個步態周期的特征序列，將兩個樣本匹配，則SA和SB的幅值失真距離表示為：參考樣本SA及樣本SB中的一個幅值序列匹配路徑如圖4 所示，相應的匹配曲線如圖5 所示。經動態時間規整后，兩條幅值序列具有相同的特征點數，且對比更加直觀，不同人的特征點具有很大差異性，將不同幅值序列的特征點都規整到12 個點，為BP 神經網絡的輸入提供了數據來源。

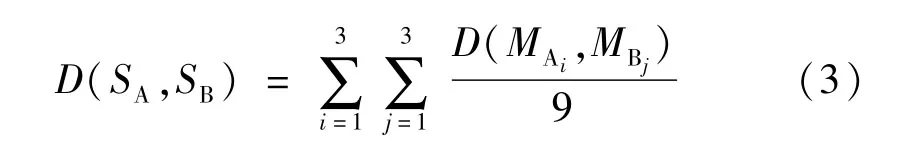
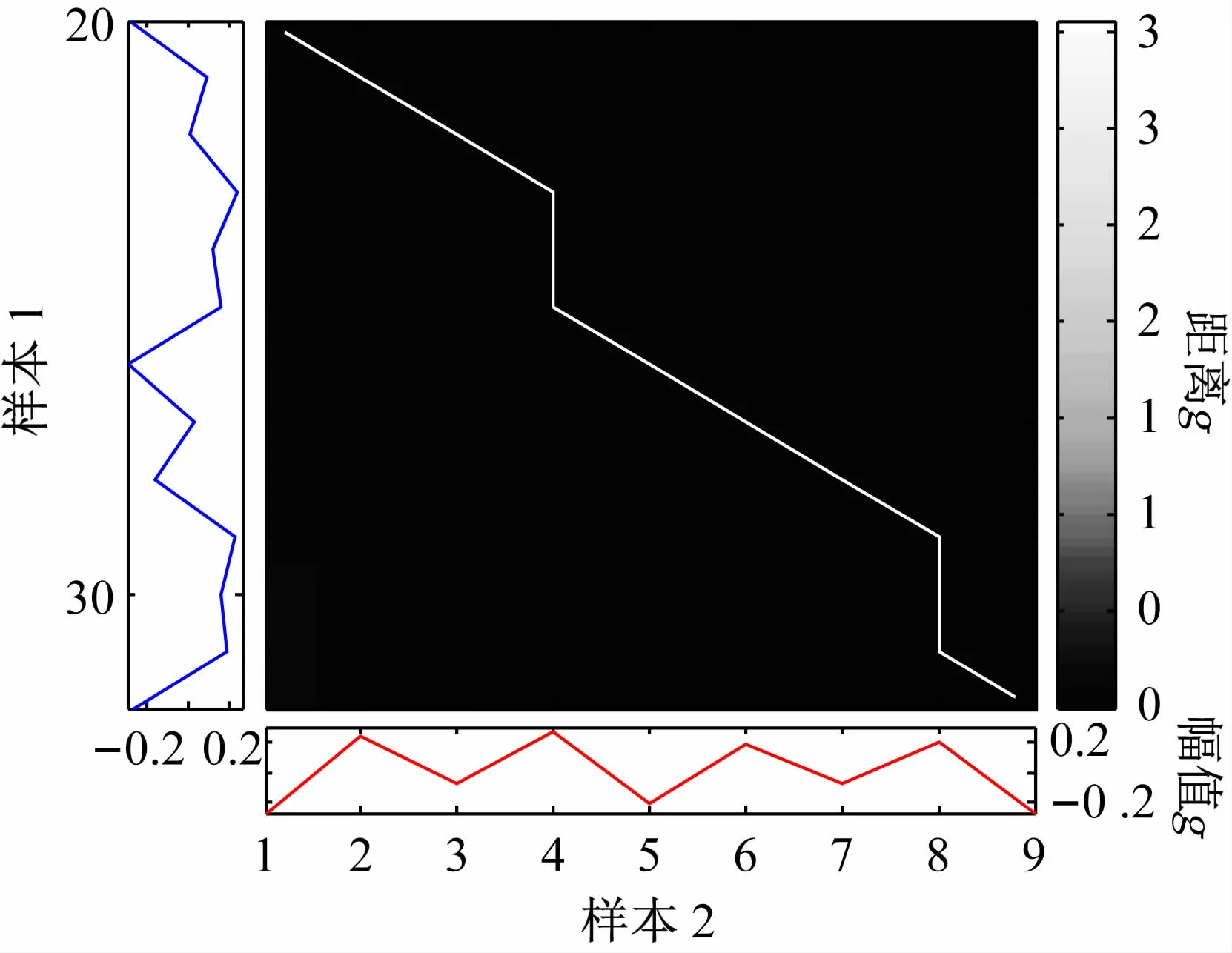
圖4 幅值序列的匹配路徑

圖5 幅值序列的匹配曲線

2.3 改進的BP神經網絡

BP神經網絡設計需確定隱含層的數量及輸入層、隱含層、輸出層節點數。在BP 神經網絡中，雖然隱含層層數的增加能提高識別率，但神經網絡的復雜度大大增加。考慮到可穿戴設備中處理器的計算能力較低，為保證步態識別的實時性，本實驗只選擇一個隱含層。

實驗以一個步態周期為基礎，第1 層為輸入層，含有17 個輸入節點，構成17 維輸入向量（X1，X2，…，X17）T，分別表示17 個特征參數，特征參數包括經過動態時間規整后的12 點幅值序列、正負（1／0）輸入、標準偏差STD、步長L、步頻c、步速v。設f為采樣頻率，n為一個步態周期的采樣點數，則標準偏差STD、步長L、步頻c、步速v的計算公式如下：

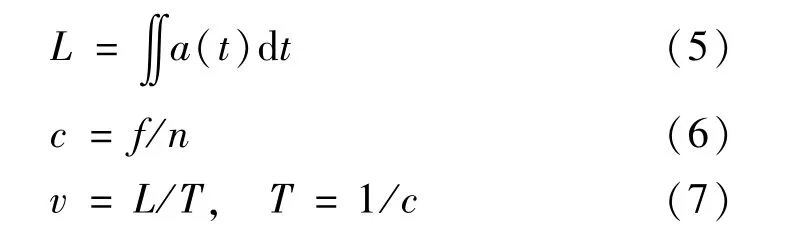
第2 層為隱含層，設l為輸入層的節點數，n 為輸出層的節點數，則一般情況下隱含層節點數m 可表示為：

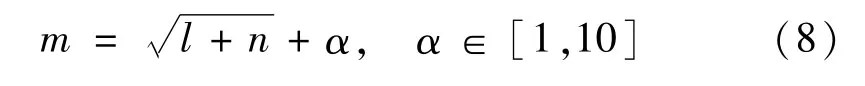
確定隱含層節點數范圍后，通過實驗訓練，確定本實驗隱含層節點數為7，激活函數采用連續可微且更接近生物神經元信號的S型激活函數。

第3 層為輸出層，含2 個輸出節點，構成2 維輸出向量（Y1，Y2）T，即（0，1）T表示真實用戶；（1，0）T表示仿冒用戶。

綜上所述，本文的算法流程圖6 所示。

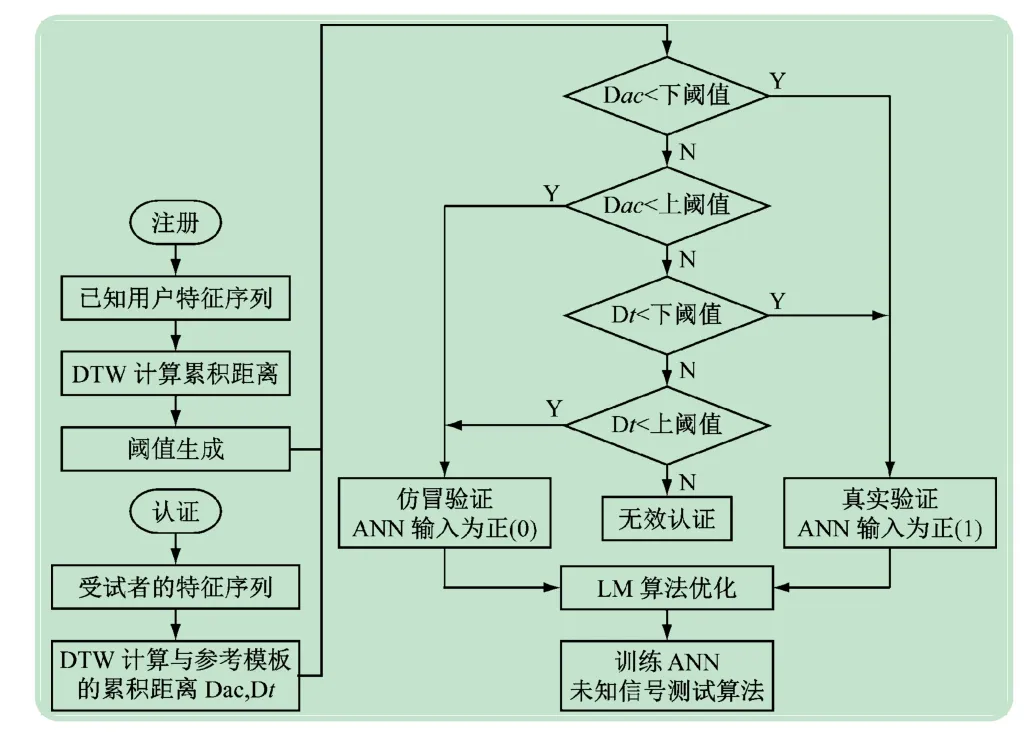
圖6 DTW-ANN算法流程圖

根據圖6 所示的流程圖，DTW-ANN 算法的步驟可以簡化為以下兩個步驟：

（1）注冊階段。采集已知用戶的樣本并提取特征序列，用DTW 成本函數計算幅值序列和時間序列的累積距離，分別作擬合函數生成閾值，并將擁有不同特征數的特征序列規整到12 點，解決了BP 神經網絡輸入結構固定的問題。

（2）認證階段。采集受試者的樣本并提取特征序列，用DTW成本函數計算與參考樣本幅值序列與時間序列的累積距離Dac，Dt，并將其通過二級認證系統初步識別，運用LM 算法，即調節變量因子u 優化BP神經網絡，將DTW規整的固定長度特征，正負輸入及步長、步頻、步速作為BP 神經網絡的輸入節點進行訓練及測試。該方法相比單一的DTW，能實現更高精度的步態識別，并且LM算法能快速收斂，確保系統的實時和準確性。

3 結果與分析

本次實驗采樣頻率設置為40 Hz，采集了10 名志愿者（6 名男性，4 名女性）的步態數據。數據采集時，將數據采集裝置固定在志愿者腰帶右側的位置。志愿者按照其步行習慣，在水平過道上直線行走1 min，3名志愿者采集5 d共采樣25 次，7 名志愿者采樣5 次。設A，B，C，D分別表示不同的志愿者；SA，SB，SC，SD分別代表不同志愿者的參考樣本；SA1，SA2，SA3，SA4，SA5，SA6分別表示志愿者A 的其他6 個步態樣本。通過DTW算法分別計算同一志愿者樣本間的失真距離和不同志愿者樣本間的失真距離，實驗結果如表1、2 所示。步態識別時，每次選擇570 個樣本組成樣本集，其中300 個樣本來自同1 名志愿者組成正類，270 個樣本來自其余的9 名志愿者，每名志愿者提供30 個樣本組成負類。將80%的樣本用作訓練，20%的樣本用來測試，實驗結果如表3 所示。其中TP，TN表示正確分類，分別表示將原先是正類的預測為正類和將原先是負類的預測為負類；而FP，FN 表示錯誤分類，分別表示將原先是負類的預測為正類和將原先是正類的預測為負類。圖10 為根據BP 神經網絡訓練結果繪制的受試者工作特征（Receiver Operating Characteristic，ROC）曲線圖。

表1 用DTW計算同一志愿者失真距離

表2 用DTW計算不同志愿者失真距離

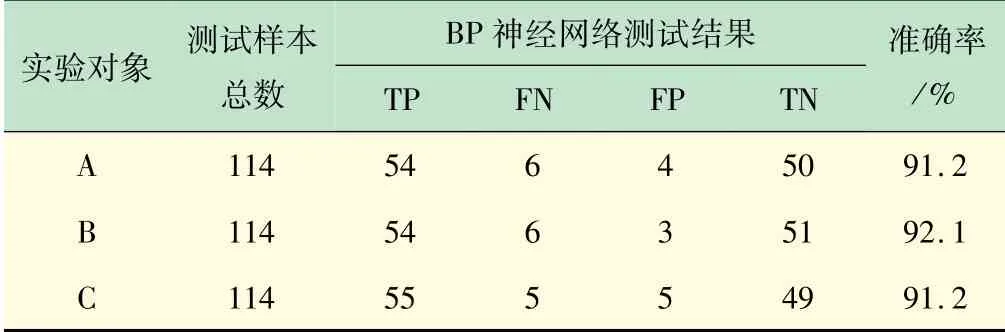
表3 測試樣本的步態識別結果

由表1 及2 可知，同一志愿者兩個樣本幅值失真距離和時間失真距離均比不同志愿者樣本小，可通過抽取一定數量樣本，設置成本函數閾值，自動初步驗證樣本。將類內最大距離作為下閾值，類間最小距離作為上閾值，當測試樣本與參考樣本失真距離小于下閾值時，則認為同一人；而大于上閾值時，則認為是不同人。根據采集的數據樣本，計算得幅值的上閾值為0.561 9，下閾值為0.425 8，時間的上閾值為0.081 4，下閾值為0.054 5。

設置BP網絡最大訓練次數為10 000 次，目標誤差為0.001，學習率為0.01，分別用標準BP算法、擬牛頓法、LM算法對網絡模型進行訓練。訓練結果如圖7～9 所示。由圖可知，標準BP算法即使訓練到10 000步，均方誤差仍為26.28 ×10-3，不能達到理想目標，存在收斂速度慢，容易陷入局部最優解的問題；擬牛頓算法在462 步時達到收斂，均方誤差為999.65 ×10-6；LM算法僅需23 步就能訓練完成，此時均方誤差為935.04 ×10-6。因此，采用LM對標準BP神經網絡改進，在兼顧BP網絡識別準確率的情況下，大大減少了訓練時間，節省成本的同時提高了效益。

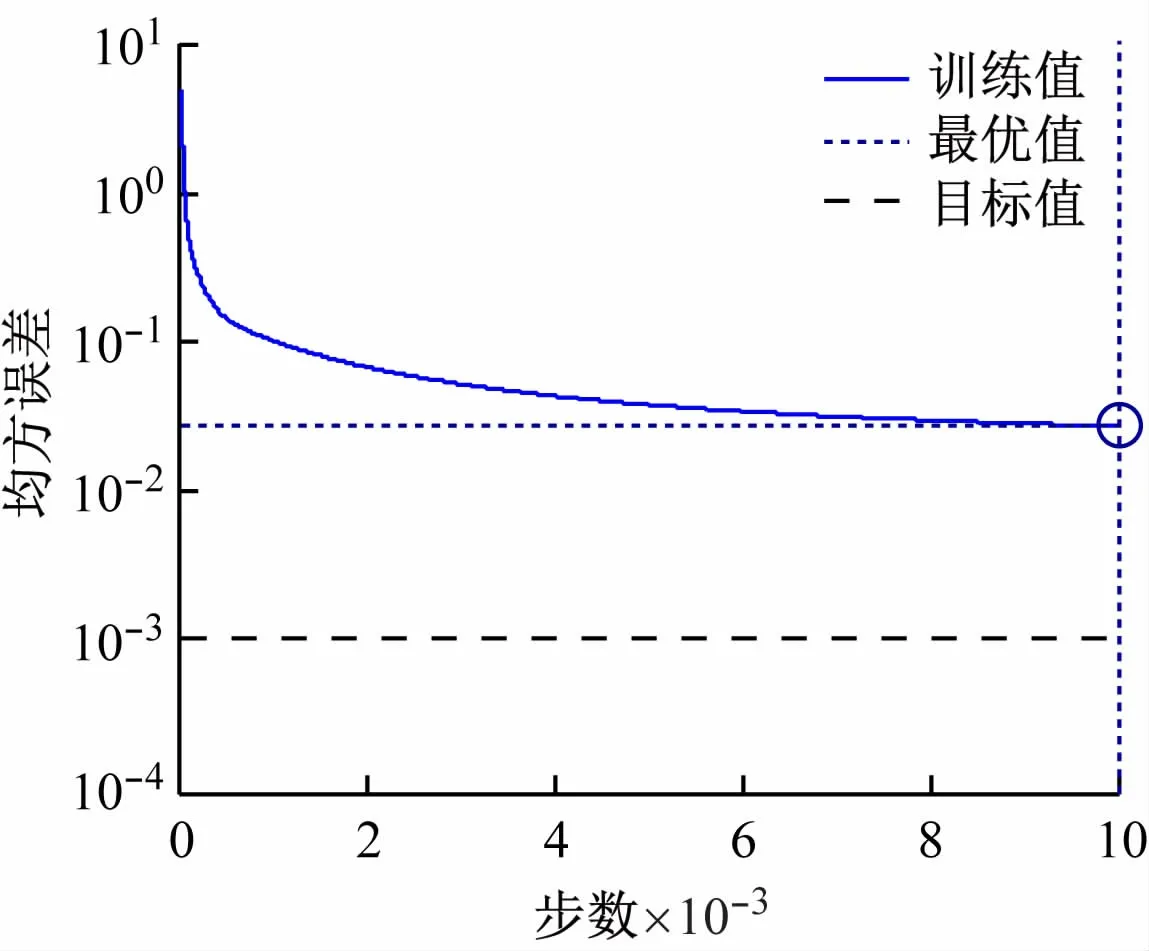
圖7 標準BP算法步態識別訓練誤差曲線

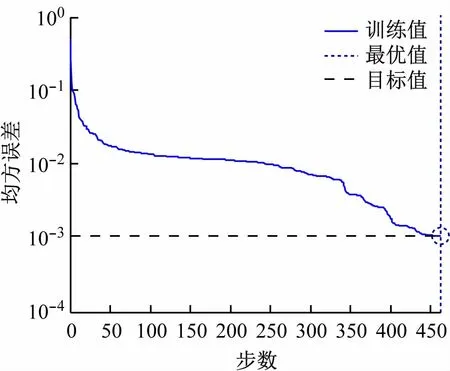
圖8 擬牛頓算法步態識別訓練誤差曲線

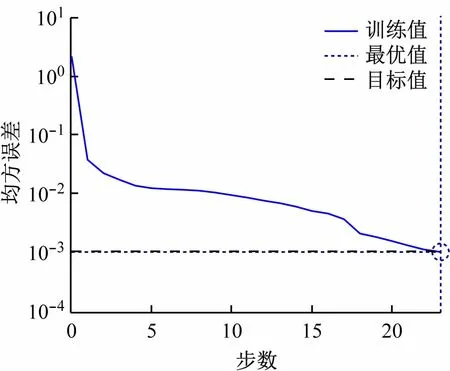
圖9 LM算法步態識別訓練曲線

將BP神經網絡模型的預測結果從小到大排序并把每個概率作為閾值，可以得到多個混淆矩陣。對于每個混淆矩陣可以計算得到特異度（False Positive Rate，FPR）和靈敏度（True Positive Rate，TPR）兩個指標。以FPR為x軸，TPR 為y 軸作圖得ROC 曲線；以（0，1）為起點，（1，0）為終點做一條直線，兩條線的交點即為EER。由表4 及圖10 可知，對于不同的人，本文平均步態識別率可以達到91.5%，EER 為9.1%。相比現有的步態識別算法，識別的準確率大大提高并且有效降低了EER，表明本文所提出的方法具有一定的實用性和有效性。

表4 不同算法結果對比

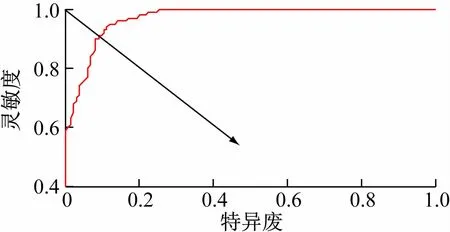
圖10 ROC曲線圖

4 結 語

本文設計了低成本且通用性強的步態數據采集裝置來獲取步態加速度信號，在低采樣率前提下，提出了一種動態時間規整和人工神經網絡相結合的步態識別方案。該方法通過DTW 算法，對步態特征序列進行規整，求得失真距離，通過閾值判斷自動實現對樣本的初步驗證，將規整后的特征參數與步長、步速、步頻特征相結合，利用LM 改進的BP 神經網絡實現步態識別。與現有方法相比，該方法兼顧采樣率和識別率，有效降低了成本且具有較好魯棒性，符合未來安全認證要求，具有信息安全保護方面的應用價值。