有限元SN中子輸運模擬的區域分解并行

郭海兵，黃洪文，馬紀敏，丁文杰

(中國工程物理研究院 核物理與化學研究所，四川 綿陽 621900)

中子輸運方程是反應堆物理分析的基礎，它通過描述大量微觀粒子運動所遵循的微分-積分關系，確定粒子在時間、能量、幾何空間和速度相空間等7個維度上的分布[1]。求解中子輸運方程獲得中子角通量密度，便能計算出中子與原子核的各類反應率，進而得到系統的物理性能。通過數值離散偏微分方程并解得離散點上近似值的確定論方法，具有計算速度快、可獲取物理量的精細場分布、可高效多物理耦合等優點。確定論方法采用分群方式離散能量變量，對方向變量的處理則衍生了多種方法，目前研究和應用最廣泛的是離散縱標(SN)法。

對空間變量的離散可分為結構化網格和非結構化網格兩種，結構化網格在對復雜結構的高保真建模方面存在明顯缺陷。基于非結構網格的有限元方法在中子輸運求解中應用后，復雜結構的高保真建模和計算得以解決[2-4]，但計算量相對較大。因而在全堆芯計算和大空間輻射屏蔽問題中，必須借助現代大規模并行計算技術才能實現大型復雜結構問題的高保真模擬分析[5-6]。

采用共享內存的多線程并行方式(OpenMP)容易實現SN方法下各獨立離散方向的并行求解，但受制于單臺計算機的CPU數量和內存資源，這種方式的并行規模及允許網格量有限。對幾何空間進行區域分解，并采用獨享內存的多進程并行方式(MPI)計算，則能大幅擴展并行規模[7-8]。

并行自適應非結構網格應用框架(JAUMIN)是北京應用物理與計算數學研究所針對科學計算中的非結構網格應用而開發的數值模擬支撐平臺，通過封裝高性能數據結構、集成成熟數值算法、屏蔽大規模并行和網格自適應技術，加速可使用現代高性能計算機的應用程序研制[9-11]。基于最小二乘有限元和SN方法[12]的中子輸運程序ENTER是自主開發的用于支持新型反應堆和次臨界包層設計的數值模擬軟件，銜接成熟的CAD建模-網格劃分前處理軟件和數據可視化后處理軟件，輕松實現復雜結構的高保真建模、高精度模擬和靈活的數據分析。

采用JAUMIN框架進行區域分解和多進程并行，通過改造并行流水線掃描算法，實現了ENTER程序的高效并行，通過系列基準問題和若干大型問題驗證了程序的正確性和并行效果。本文將具體介紹基于有限元和SN方法求解中子輸運方程的算法以及區域分解和并行掃描的實現機制，最后通過部分計算案例展示ENTER程序的計算精度和并行計算能力。

1 中子輸運方程及其有限元SN求解

定常條件下，多群形式的中子輸運方程[1]可寫為：

g=1,2,…,G

(1)

式中：φg=φ(r,g,Ω)，為能群g在位置r處沿方向角Ω的中子角通量密度；Σt,g=Σt(r,g)，為能群g的宏觀總截面；Sg=S(r,g,Ω)，為能群g的各源項之和，包括散射源項Ss,g、裂變源項Sf,g和獨立外源項Se,g。

Sf,g和Se,g均易于計算和處理，本文不作贅述，重點討論Ss,g在SN方法下的表達形式。散射截面是散射前后運動方向間夾角的函數，將散射截面和中子角通量密度分別以有限階的勒讓德函數和球面諧函數近似展開后，得到散射源項表達為：

(2)

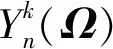
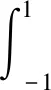
(3)

(4)

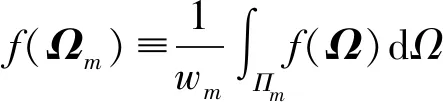
(5)

從而，選定1組離散方向并確定相應的權重值{Ωm,wm}后，即可將式(3)和(4)的積分轉化為求和，進而將式(2)轉化為以離散方向處的中子角通量密度φg,m=φ(r,g,Ωm)為待求解量的方程。在直角坐標系下，離散方向Ωm=(μm,x,μm,y,μm,z)處的多群中子輸運方程為：

g=1,2,…,G

m=1,2,…,M

(6)

在進行有限元離散和求解時，由于式(6)是非自伴隨的，直接應用標準Galerkin加權方法可能會引起解的振蕩，應采用迎風Petrov-Galerkin(SUPG)[13]等加強穩定性的方法，或采用間斷有限元(Discontinuous Galerkin, DG)[4]、最小二乘有限元(Galerkin Least Square, GLS)[12]等方法求解，在高維問題中GLS方法實現較簡便且計算量較小，以下即對GLS方法簡要說明。

有限元方法是在離散單元內將待求變量φg,m(r)近似表達為1組特別選定的基函數{N(r)}的線性疊加，單元內各結點的變量離散值向量Φg,m即作為基函數的系數：

(7)

式中，N為單元的基函數組成的行向量。

L(φg,m)=Sg,m

(8)

(9)

代入算子L的表達式，并展開積分式，化簡得到式(6)的矩陣形式離散求解方程：

(μm,kμm,iHk,i+Mt,g+μm,kGg,k)Φg,m=

(10)

式中，以指標符號形式簡寫了求和。對于不含獨立外源的問題，式(10)對一維和二/三維幾何是通用的，但一維下所求解變量的物理意義略有不同，以表達式說明：

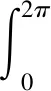
(11)

對于獨立外源項，由于其不依賴中子角通量密度φg,m，因而基于式(5)的轉換后，計算式在一維下比二/三維下多了因子2π。除此之外，不同幾何維度的計算方法和流程完全一致。

式(10)采用源迭代法求解，在每步迭代中還可采用擴散綜合加速(DSA)算法[14-15]對中子通量密度(標通量)和中子流密度(中子角通量密度的1階球諧分量)進行修正，以使迭代更快收斂。或基于中子數守恒的思想，采用角度再平衡方法進行加速。

2 區域分解及并行掃描算法

所謂區域分解，即是把計算問題的幾何結構劃分成多個相對小的子區域，將各子區域分配給不同的CPU核進行求解，一方面減小了求解方程組的規模，另一方面通過并行增加了單位時間運算量，從而提高計算速度。區域分解算法的關鍵是通過子區域之間的數據傳遞，使得分區并行求解(可能需子區域間迭代)的結果與全域整體求解的結果一致。

區域分解后會產生新的界面(子區域邊界)，這些界面原本處于計算域內部而不需關注，但成為子區域邊界后就需指定合適的邊界條件，以使可在子區域上求解方程。具體來說，采用SN方法求解中子輸運方程時，需為每個方向的入射邊界指定中子角通量密度。JAUMIN框架基于重疊型區域分解算法來完成子區域間數據傳遞，即將每個子區域的劃分邊界向相鄰子區域中延伸1層網格，形成被稱為影像區的重疊區域，用于獲取相鄰子區域相應結點的數據[16]。重疊型區域分解算法的理論基礎是Schwarz交替法及Lions等對它的并行化拓展[17-18]。子區域及其影像區合稱為網格片，輸運方程的求解是在網格片上進行的。以一維幾何下兩個相鄰子區域的情況作示意說明，如圖1所示。

控制各子區域的網格單元數量基本相等的情況下，采用JAUMIN框架對方形區域的非結構網格進行區域分解形成的16個子區域如圖2所示。

應用程序在JAUMIN框架上實現并行的原理是框架將所有網格片的初始化、并行計算、數據傳遞、歸約同步等操作封裝為積分構件，在網格層上通過調用這些積分構件形成完整的并行計算流程，依托C++語言的類繼承和虛函數這兩個重要機制，用戶只需在繼承類的虛函數中具體實現特定物理問題在單個網格片上的初邊值條件和數值求解、在網格層上的歸約同步和迭代操作，則原有并行計算流程中的相應模塊被繼承類的用戶函數替代，框架的并行機制和計算流程保持不變而實現不同問題求解[19]。ENTER程序基于JAUMIN框架的區域分解并行架構如圖3所示。

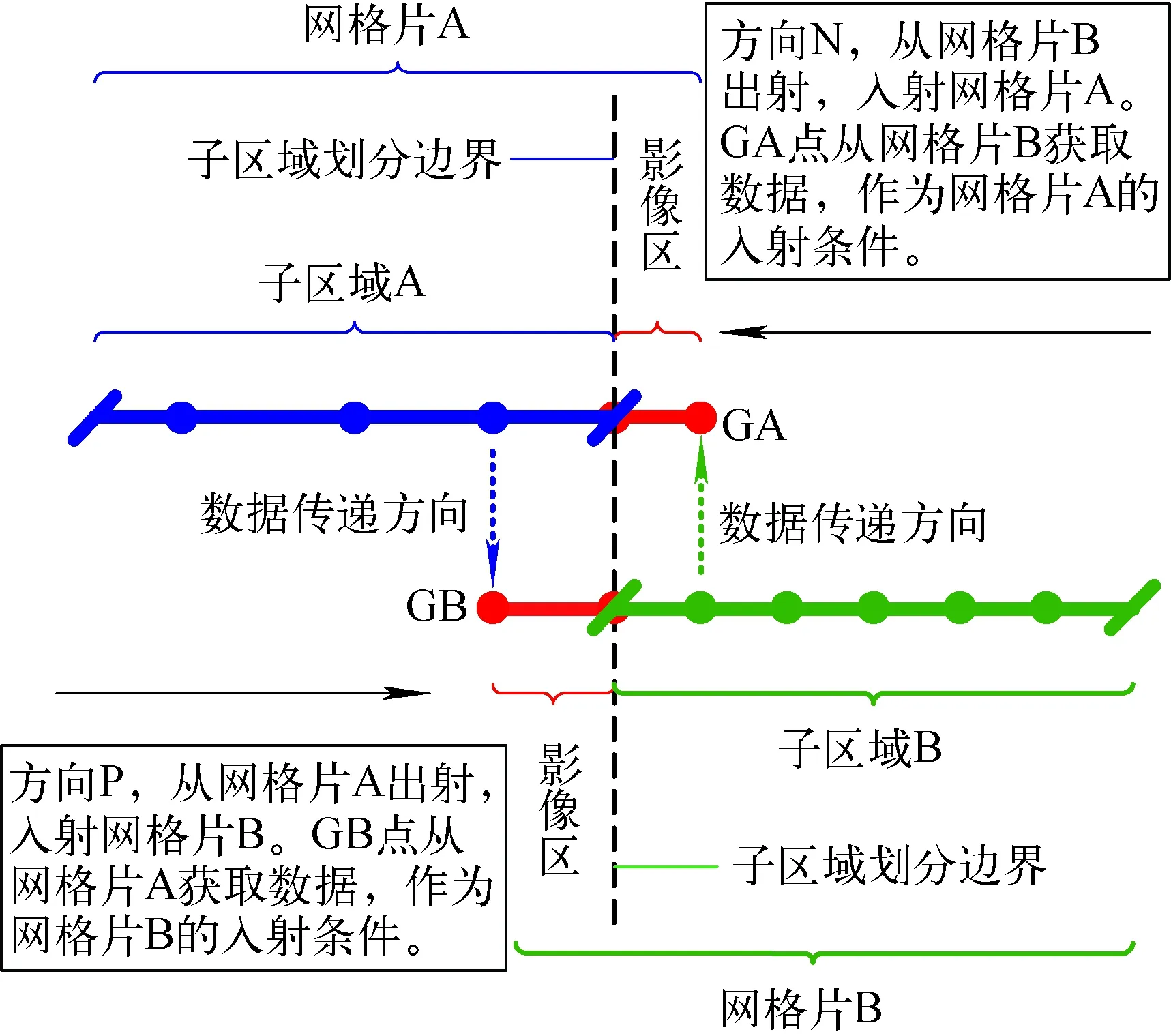
圖1 網格片影像區及數據傳遞示意圖Fig.1 Sketch of ghost areas and data transfer scheme between mesh patches

圖2 非結構網格區域分解示意Fig.2 Illustration of domain decomposition under unstructured mesh

由于SN輸運方程(式(6))的求解具有方向性，只有入射邊界(Ωm·n<0，n為邊界外法線向量)上的變量已知時，網格片內各離散點才可求解。對于真空邊界，該定解值為0；對于反射邊界，該定解值為對稱出射方向在反射點的中子角通量密度，因此需先求解對稱出射方向方程；對于影像區邊界，該定解值由該方向上游相鄰網格片傳遞過來，需先求解上游網格片。

因而對幾何空間做區域分解后，各網格片并非完全獨立可解的，本文借鑒間斷有限元方法中使用的并行流水線掃描算法，將各網格片與所有離散方向進行對應組合，對每個網格片獨立判斷未求解的各離散方向是否具備可求解條件，只要有1個方向可求解，則將該網格片加入并行隊列，當前計算步只并行求解隊列中的網格片上可求解方向對應的輸運方程。網格片上的某個方向完成求解后，將更新下游若干個相鄰網格片該方向的可求解條件。每個離散方向最上游的網格片將首先具備求解條件，如果某網格片上沒有離散方向具備求解條件，則將跳過當前計算步，等待其邊界上可求解條件被更新。這樣分批次并行求解，直到所有網格片上的所有方向完成求解[8-10]。

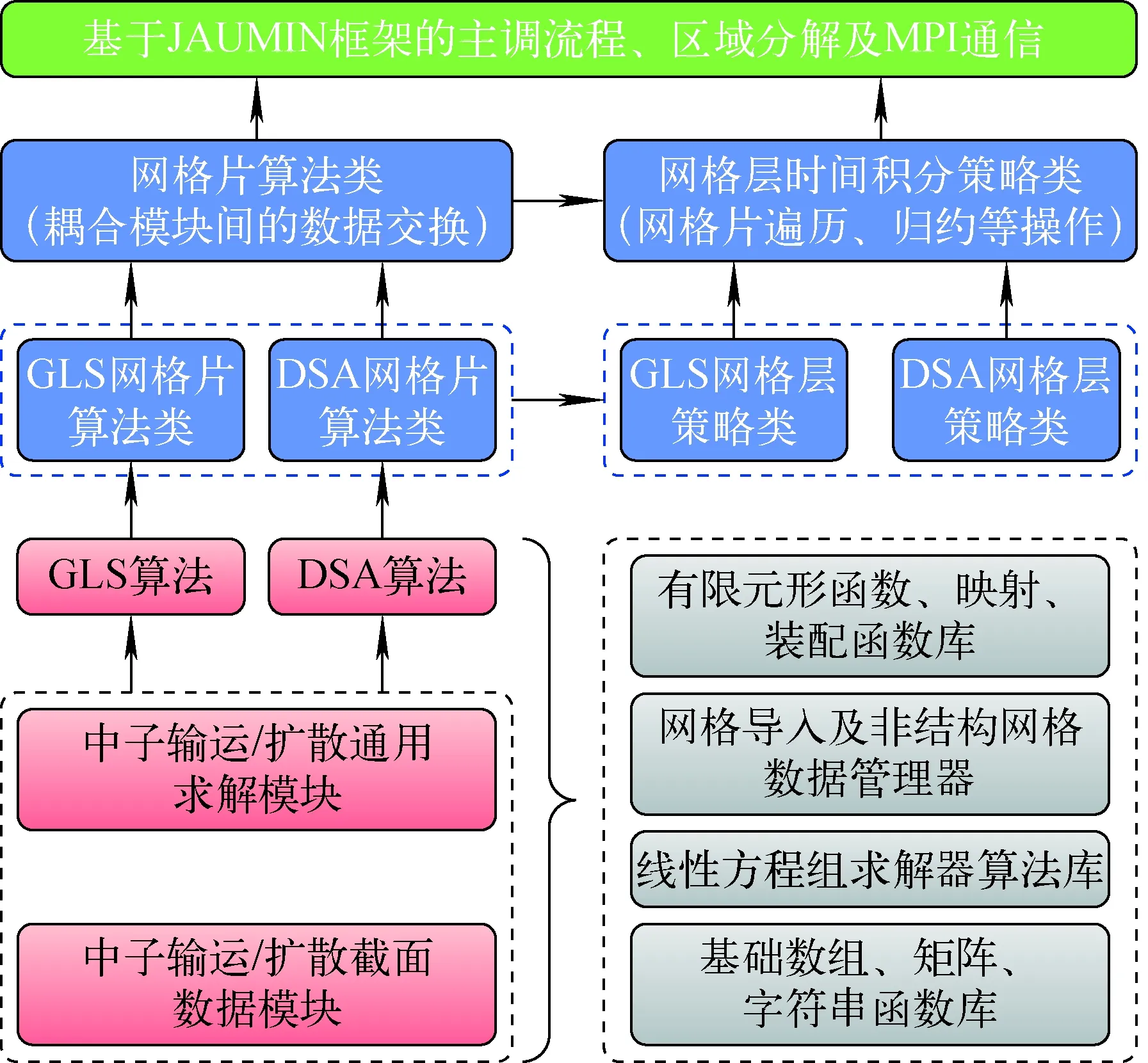
圖3 ENTER程序基于JAUMIN框架實現并行的總體架構Fig.3 Framework of parallel code ENTER based on JAUMIN infrastructure

在每個并行計算步中，各網格片上求解的離散方向一般不同。以圖2所示的二維16個網格片劃分和4個離散方向(對應S2)為例，對并行掃描算法在每個計算步中各網格片求解的方向號說明列于表1，表中“#”表示網格片編號，“×”表示當前計算步跳過，“√”表示當前網格片上的所有離散方向求解完成。

表1 并行掃描算法在每個計算步中各網格片求解的方向號Table 1 Solving direction number of all patches under each step of parallel sweeping algorithm

每個CPU可處理1個或多個網格片，出于負載平衡考慮，使用的CPU數應為網格片數量的約數。無論是針對結構化網格的KBA掃描算法[20-21]，還是針對非結構網格間斷有限元的并行流水線掃描算法[9]或有向圖掃描算法[22-23]，表達方式和程序實現形式不同但基本思想一致，即對入射邊界上變量值已知的基本求解單位做同步計算，只不過結構化網格下依賴關系完全明確，有向圖算法根據網格依賴關系預先對掃描計算順序作抽象后進行分解并行。本文的掃描算法也是據此而來，采用無向區域分解和對網格片的并行掃描，基本求解單位是網格片與離散方向的組合，并行粒度相對較大，通信開銷較小，但對入射邊界是否滿足求解條件的判斷則更復雜。

由于區域分解形成的網格片邊界不規整，對某些離散方向，網格片之間的依賴關系復雜甚至相互依賴，因此會出現某些網格片上的某些方向需多次求解的現象，這樣才能完成可求解條件向下游網格片的傳遞。掃描算法在單步求解中存在的偏差會隨著源迭代求解過程逐漸減小，并最終獲得收斂的結果。但隨離散方向數的增多，掃描過程會變得更復雜，雖然可并行度提高了，但掃描過程中出現網格片互相依賴的情況更頻繁。

3 正確性驗證和并行性能分析

通過對系列基準問題的計算對比完成了ENTER程序驗證。現通過部分問題的結果，分析ENTER程序的精度和并行性能。對問題的完整描述及截面參數參閱相關文獻[24-28]，源迭代收斂準則為keff殘差<1×10-5且中子通量密度的均方根偏差<1×10-4。

ISSA基準題是一維、單群、P0階散射的臨界問題，通過在y軸和z軸方向設置反射邊界，可將該問題擴展為二維和三維問題。對該問題在不同條件下的計算結果的對比列于表2，ENTER計算結果為網格無關解，即通過多次加密網格獲得一致結果。與參考值相比，S6條件下keff的最大偏差為4.1×10-4，S16條件下的最大偏差為1.7×10-4。由于一維與二/三維采用的離散求積組不同，在數值積分精度上不同，因此對于S4及以上條件，二/三維的結果接近，但與一維略有差異。

圖4展示了兩個外源問題的計算結果對比，圖4a為一維、2群、P3階散射各向異性問題[25]，圖4b為二維、2群、P1階散射深穿透問題[26]，兩個問題均采用S8條件計算。從圖可見，在中子通量密度跨越7個量級的情況下，計算結果仍與參考值能保持較好的一致性。

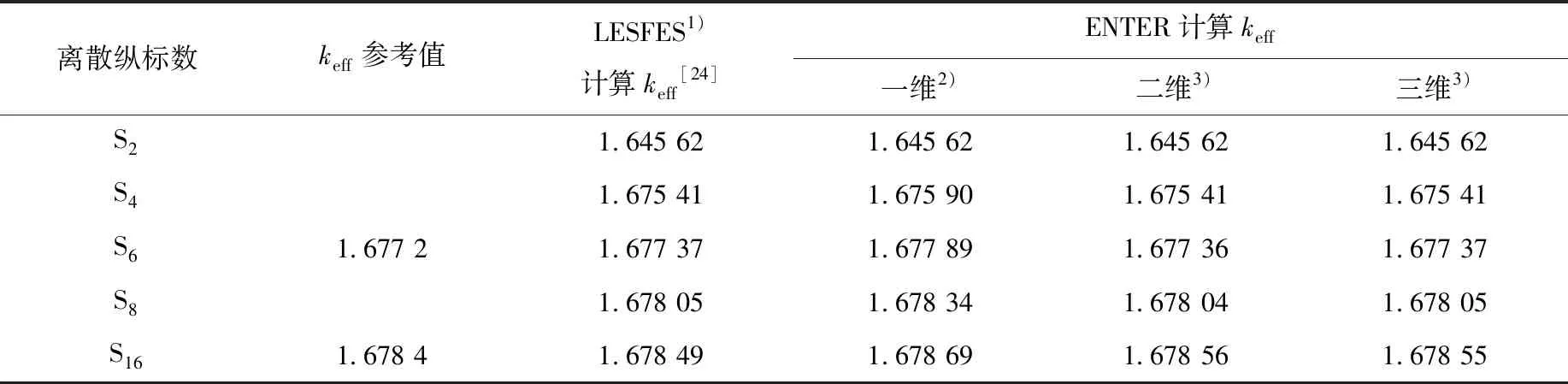
表2 ISSA基準題keff計算結果對比Table 2 Comparison of keff results for ISSA benchmark

注：1) 西安交通大學巨海濤等[24]開發的最小二乘有限元SN中子輸運程序

2) 采用GAUSS求積組

3) 采用偶階矩條件的全對稱求積組[29]

圖4 外源各向異性和深穿透問題計算結果Fig.4 Comparison of external source problem and deep penetration problem results under heterogeneous scattering condition

外邊界全部為反射條件的問題對SN方法具有特殊的意義，此時每個離散方向在其他所有象限中均存在1個耦合關聯方向，所有離散方向都不能獨立求解，并且中子通量密度沒有唯一解，計算過程中需進行循環迭代和多次歸一化處理。BWR柵元問題是二維、2群、P0階散射的臨界基準題，外邊界全部為反射條件[27]。采用ENTER程序S8和S16計算的keff與參考值的相對偏差分別為1.2×10-4和4.9×10-5，獲得的兩群中子通量密度分布如圖5所示。

對Takeda和Ikeda發表的三維小型LWR堆芯基準題[28](1/8堆芯，控制棒插入)進行精細網格劃分，并采用不同離散縱標數求解，通過強擴展并行測試來分析ENTER程序的并行性能(表3)。該問題為2群、P0階散射，采用四面體網格劃分，1/8堆芯單元總數為1.37×105。定義自由度數=能群數×方向數×變量點數，則S4條件下最大自由度數為9.91×106，S8條件下最大自由度數為3.30×107。

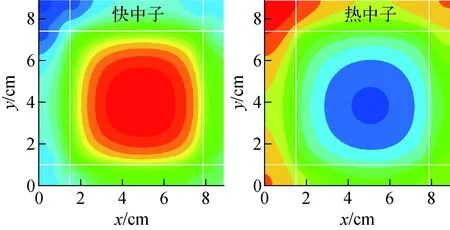
圖5 BWR柵元問題的兩群中子通量密度分布Fig.5 Contours of fast and thermal neutron flux density distribution for BWR cell problem

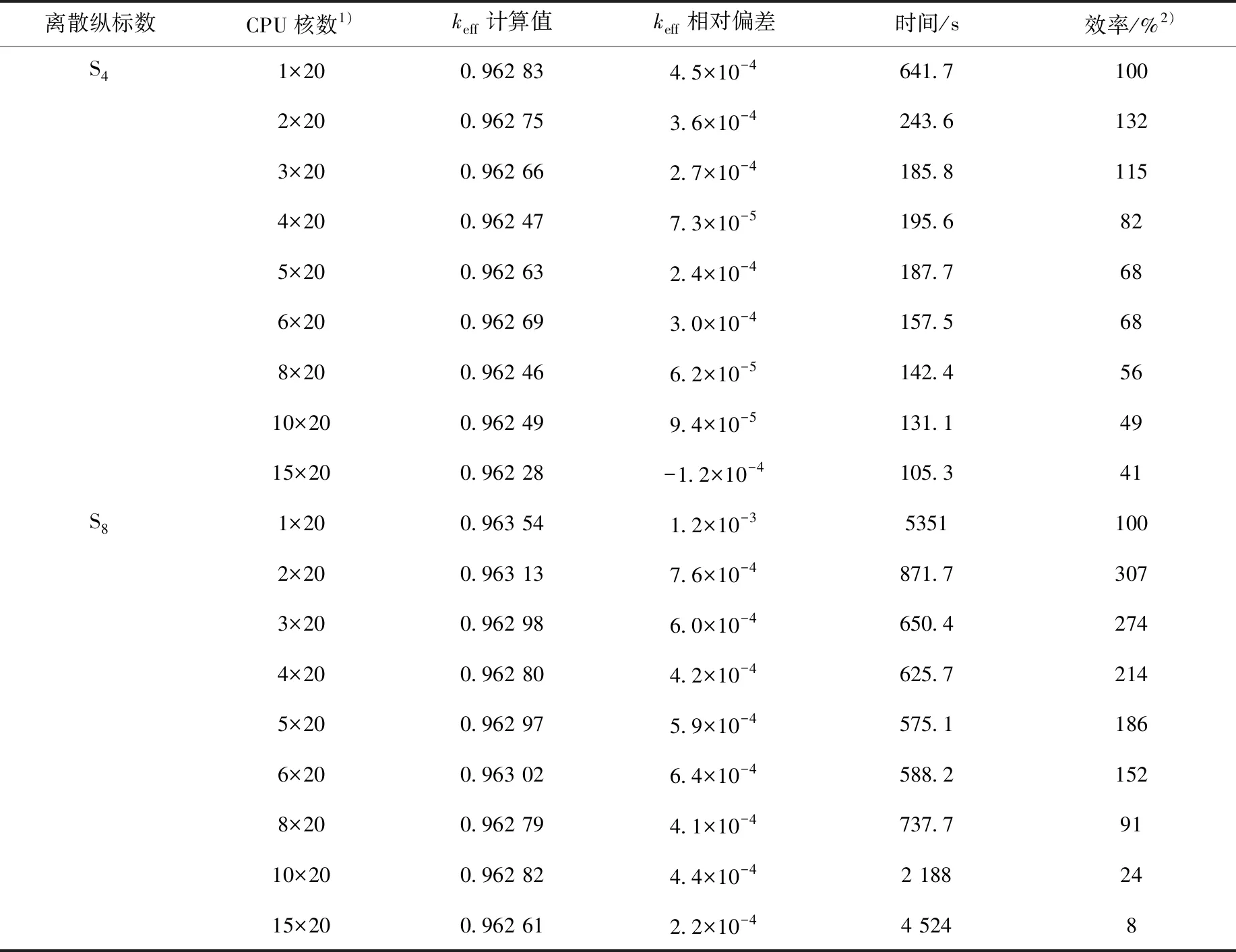
表3 小型LWR堆芯基準題計算結果及并行效率分析(keff參考值為0.962 4±0.000 5)Table 3 Simulation result and parallel efficiency analysis for small LWR benchmark problem(reference value of keff is 0.962 4±0.000 5)

注：1) CPU核數記為NP，表示使用N個節點，每個節點使用P個進程，每個進程處理1個網格片

2) 以最少CPU核數(CL)時的計算時間(TL)為參考，設定并行效率為100%，隨著并行CPU核數(CN)的增加，實際計算時間(TN)對應的并行效率為CLTL/CNTN

從表3的結果可見，該問題在S4條件下保持了很好的并行擴展效率，而在S8條件下并行核數高于160后效率下降很快。這主要是兩方面原因造成的：一是離散方向數較多的情況下，當存在反射邊界條件時，網格片之間的依賴關系隨網格片增多而更復雜，掃描算法更耗時間；二是問題規模不大時，劃分網格片越多，每個網格片內部的單元數越少、影像區單元數越多，計算量增加且通信耗時占比更高。

對包含169個六棱柱組件的FBR三維堆芯基準題(控制棒半插入)[28]進行全堆芯輸運計算，采用4群、P0階散射截面，離散縱標數S8。基于三棱柱網格，并采用1次全局網格自動加密(將所有的網格邊二分，三維下1個單元被切分為8個小單元)和不同的CPU核數，各區域平均的中子通量密度列于表4，獲得的各群中子通量密度剖面分布如圖6所示，計算得到的keff結果和耗時列于表5。

從表4、5可見，基于ENTER并行程序對該大規模問題的模擬結果是準確的，區域平均的中子通量密度與SN文獻值相比，ENTER的計算精度顯著更高，與MCNP參考值符合很好，最大偏差出現在控制棒區域第4群，這可能是該能群的局部吸收率較大而ENTER求解時局部網格密度不夠造成的。對問題的計算時間是可接受的，計算結果的精度對網格密度較敏感，這主要是由于控制棒周圍的中子角通量密度梯度較大，目前采用的是一階線性/雙線性單元，高網格密度才能準確描述通量的空間分布。后續需進一步考慮引入高階單元和局部自適應加密技術，以實現較少網格量下獲得高精度結果。

表4 區域平均中子通量密度與參考值[28]的比較Table 4 Comparison of zone-averaged neutron flux density between simulation results and reference values

注：表中( )內的值，對于MCNP參考解為統計誤差，其他則為與MCNP參考解的相對偏差

圖6 六棱柱FBR堆芯的中子通量密度二維剖面分布Fig.6 Contours of neutron flux density distribution for hexagonal FBR core

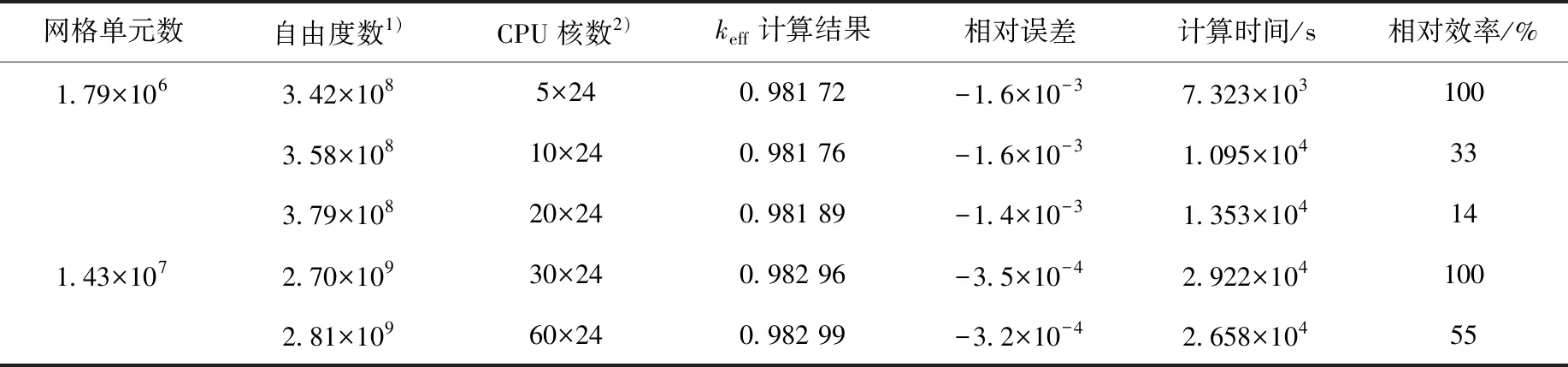
表5 六棱柱FBR堆芯計算結果及時間(keff參考值為0.983 3±0.000 4)Table 5 Simulation result and time cost of hexagonal FBR core(reference value of keff is 0.983 3±0.000 4)

注：1) 網格片數增多會使得影像區的總結點數增加，因而在相同的網格下，劃分網格片越多，自由度數越大

2) 天河Ⅱ號單個節點的CPU核數為24

4 討論及結論

區域分解是對輸運方程的空間變量的并行處理，并不排斥對離散角度變量的并行求解，并行掃描算法融合了空間和角度兩個變量的并行度，因而當網格片上有多個方向同時具備求解條件時，這些方向之間也是可并行求解的。目前的ENTER程序是基于MPI的空間并行，每個網格片每步只能求解1個方向，因而網格片上的角度并行需采用第2級的OpenMP方式實現。

非結構網格最小二乘有限元方法在區域分解并行機制下可解決大型復雜結構堆芯的輸運計算問題，獲得準確的堆芯參數分布，在2.81×109自由度規模下計算時間約7.4 h是可接受的，具有一定的工程應用價值。但該方法尚不能獲得大規模的并行擴展，特別是在方向數較多(S8以上)的情況下，隨著劃分網格片數量的增多，網格片之間的依賴關系變得復雜，并行效率急劇下降。同樣由于該原因，在并行條件下的計算結果與串行結果沒有取得完全一致。

間斷有限元方法是克服以上困難的有效途徑，因為間斷有限元方法以單元與方向的組合為基本求解單位，且單元邊界平直，不存在兩個單元互相依賴的問題，因而有望在這種小的粒度下實現大規模的并行，借助有向圖掃描算法可能獲得較高的并行效率。網格局部自適應加密和高階形函數的應用，也是后續值得研究的內容，可減少初始網格量并快速獲得網格無關解。

在學習和使用JAUMIN框架的過程中，得到了中國工程物理研究院高性能數值模擬軟件中心的楊章等的指導和幫助，在此對其編程框架團隊表示感謝。