壓裂水平井產能預測方法研究進展

李旭飛

（1.西安石油大學石油工程學院，陜西西安 710065；2.陜西省油氣田特種增產技術重點實驗室，陜西西安 710065）

常規油氣資源供給越來越少，油氣資源供給與需求的矛盾日益突出。國內外開發實踐證明，水平鉆井技術和大型壓裂技術是成功開發低滲透油藏的核心技術[1]。目的是改善儲層的導流能力、擴大泄油半徑，在現場得到了廣泛應用。壓裂技術成本高、工藝復雜，壓裂后對油氣井的產能預測具有重要的理論意義和經濟價值。也成為目前國內外石油工程領域熱門研究方向。壓裂水平井產能預測的研究對象為流體在裂縫內流動及裂縫外區域流動的描述以及影響因素分析等。影響壓后水平井產能因素眾多，如：裂縫空間分布、應力敏感、啟動壓力梯度、油藏內外邊界條件、完井方式等，這些因素相互影響致使壓后水平井產能預測十分困難。而壓裂后產生的高滲透水力裂縫是水平井增產的主要影響因素，因此壓裂后裂縫在地層中的空間分布模型及滲流規律是研究的重點。為準確描述壓裂后基質與裂縫間的滲流規律，國內外學者根據壓裂附近區域的改造程度提出了多種線性流模型（見表1）。求解壓后水平井產能的方法有：解析法、半解析法、數值模擬法等。本文詳述了各方法的優缺點及未來壓裂水平井產能預測的方向。

1 壓裂水平井產能求解方法

1.1 解析法

解析法多用于分段壓裂水平井的產能預測，為便于求解需對油藏和裂縫模型進行假設簡化，因此求解的模型較為理想。重點解決單井多條裂縫單相滲流問題，采用各種數學方法通過嚴謹的推導得到簡化模型的精確解。郎兆新等[5]首次基于位勢理論和勢的疊加原理，在求出單條裂縫的壓力分布后采用疊加原理建立了多條等流量裂縫壓裂水平井產能預測方程，開啟了國內壓裂水平井產能預測的先河。之后寧正福等[6]，李廷禮等[7]，羅懿等[8]在此基礎上考慮了裂縫內的滲流阻力和壓力損失、有限導流水平井筒、啟動壓力梯度和應力敏感等因素對產能的影響，這些模型是對郎兆新的產能公式的修正。該方法求解思路清晰，但求解手段較為單一，因此研究重點是尋找新的解法，如：范子菲等[9]，張建軍等[10]，Chen 等[11]應用保角變換、丁一萍等[12]應用當量井徑法、徐嚴波等[13]應用離散裂縫法分別求解了分段壓裂水平井的產能模型，促進了解析法的發展。由于低滲儲層的非均質性極強，壓裂形成的裂縫在長度、角度、導流能力等方面不盡相同，需要考慮的影響因素越來越多，方程的求解難度加大，目前使用解析法求解的文獻已不多見。

不同學者得出的結論基本一致：（1）受裂縫間相互干擾的影響兩端裂縫的產量高，中間裂縫產量最低，且存在最優的裂縫條數；（2）由于摩阻的存在水平段井筒長度并非越長越好；（3）隨著對壓裂造縫機理研究的深入，普遍認為裂縫在地下的分布具有一定傾角并與天然裂縫相互交叉形成復雜縫網；（4）需對影響壓裂水平井產能的因素綜合考慮。

不足：（1）解析法會采用一系列假設簡化實際油藏參數來建立數學模型，因此可得到簡化模型的精確解但簡化過的模型實用性有限；（2）不能考慮開發時間對產能的影響，求解方法較為單一；（3）所使用的裂縫模型較為簡單多為雙翼對稱裂縫模型且未能考慮天然裂縫網絡；（4）只能解決穩態單相達西滲流問題，在低滲儲層中計算誤差較大。

1.2 半解析法

半解析法采用點源函數理論，將裂縫離散為有限個點源，采用疊加原理、紐曼積分等方法，建立有限個點源同時存在時井底壓力分布。重點解決非穩態單相滲流問題，優點是裂縫的線性離散可以充分描述裂縫的非均質性、裂縫傾角、裂縫間相互干擾對滲流的影響。目前主要應用的源函數有：（1）1973 年Gringarten 等[14]首次將熱傳導方程里的點源函數引入滲流力學這一領域，為單重介質油藏滲流問題壓后水平井的壓力分布及產能預測提供了新思路；（2）1988 年Ozkan[15]在Gringarten源函數的基礎上應用拉普拉斯變換與數值反演方法優化了計算過程，給出了雙重介質油藏在不同邊界條件下的點源函數，得到了國內外學者的廣泛使用；（3）2007 年Valko 等[16]提出體積源函數，可以考慮源的尺寸對滲流的影響即考慮三維裂縫模型，對解決復雜縫網滲流問題也有較好的適用性。目前分段壓裂及體積壓裂是現場廣泛應用的壓裂工藝，因此國內外學者研究重點是水平井應用這兩種壓裂工藝后的產能預測。

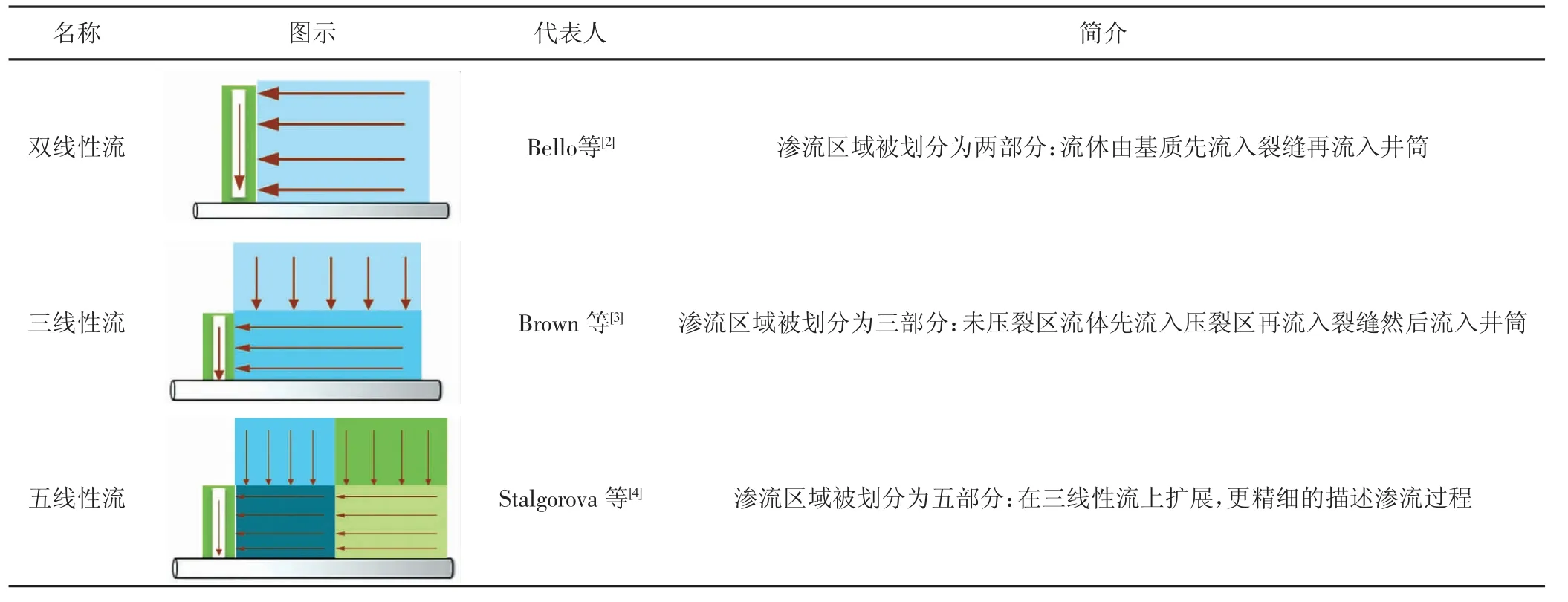
表1 線性流模型

1.2.1 半解析法求解分段壓裂水平井產能模型 分段壓裂水平井多采用多條雙翼裂縫模型進行研究，重點解決非垂直裂縫、不穩定滲流、多因素相互影響等對產能的影響。由于地層的非均質性以及鉆井和完井過程引起的應力場變化，壓裂時會出現傾斜裂縫，國內外學者基于Gringarten 及Ozkan 源函數對傾斜裂縫模型進行了研究，并通過雙對數坐標來分析試井曲線的斜率劃分不同滲流階段[17]。Luo 等[18]、任宗孝等[19]分別基于Ozkan 源函數和Gringarten 源函數，應用坐標轉換法及坐標平移原理，解決了裂縫傾角對產能的影響，建立了裂縫與水平井筒任意夾角的分段壓裂水平井產能模型。王本成等[20]基于Ozkan 源函數、正交變換法更詳細的討論了裂縫在任意傾角，非等高、非等間距條件下多段壓裂水平井壓力分布方程，認為裂縫半長越長或間距越小，裂縫間的相互干擾現象出現的越早。

在實際生產中，裂縫導流能力會隨著生產時間推移逐漸衰減，而非穩態研究中多數學者認為裂縫導流能力不變。楊正明等[25]研究了裂縫導流能力隨時間衰減及多條裂縫間干擾對分段壓裂水平井非穩態條件下對產能的影響。低滲透儲層存在應力敏感效應，嚴重影響儲層物性、流體滲流特征及井底壓力動態。Jiang 等[26]考慮分段壓裂后流體在裂縫中的非達西流且天然裂縫與水力裂縫具有不同的應力敏感系數對井底壓力動態的影響，認為非達西流對早期滲流階段影響較大，應力敏感現象對中后期滲流階段影響較大且水力裂縫中非達西流使得應力敏感效應更加明顯。

上述學者建立的裂縫模型是二維的，無法考慮裂縫內部壓力變化。Larsen 等[21]首次計算三維裂縫下的壓裂水平井產能方程，但將裂縫在z 方向上用平均壓力代替裂縫中的壓力。而Wan 等[22]認為這并不準確，在二維解析解的基礎上在z 方向上應用無窮傅立葉余弦級數將其轉換到三維裂縫模型中求解了產能方程。Lin 等[23]建立了一種平板源方法應用疊加原理求解壓裂水平井壓力分布方程，同時考慮源內部壓力變化，但它是在實空間中推導的，無法將井筒存儲效應、表皮系數等因素考慮在這種板源中。在此基礎上Jia 等[24]應用Ozkan 源函數建立了傾斜板源函數，并在拉氏空間中考慮在井筒存儲效應、表皮系數等因素影響下的有限導流傾斜裂縫井底壓力分布模型。

1.2.2 半解析法求解體積壓裂水平井產能模型 水平井體積壓裂后天然裂縫與水力裂縫縱橫交錯形成復雜縫網，在裂縫交叉處產生流體流向重定向及流量重分配的問題，這對流體的滲流規律影響很大。目前主要應用的方法是節點分析法、“星-三角形”變換法來消除縫網交叉點。Chen 等[27]總結了水力壓裂后引起的裂縫分布的多種幾何結構，包括張開型裂縫網絡、樹狀裂縫網絡、徑向多重裂縫網絡和相互正交的裂縫網絡，使用節點分析法來消除在裂縫交匯處流動相互作用。Karimi等[28]基于“星-三角形”變換方法建立了復雜縫網內裂縫間傳導率計算公式，為多裂縫交叉裂縫間傳導率的計算提供了依據。在此基礎上任宗孝等[29]考慮多條非垂直裂縫相互交叉引起的“劈分”流動，通過“星-三角形”變換計算出裂縫傳導率通式，建立了Y 字型裂縫交叉、十字型裂縫交叉以及多條裂縫交叉復雜縫網滲流模型。

不足：（1）目前廣泛使用的Ozkan 及Gringarten 源函數，難以描述復雜邊界條件的油氣藏、多相滲流以及地層的非均質性；（2）大部分文獻對分段壓裂水平井滲流模型只進行了敏感性分析如裂縫角度、長度等，而沒有對影響壓裂水平井產能的多參數進行組合優化，而體積壓裂水平井使用的縫網形狀過于簡化；（3）大部分模型為單口壓裂水平井二維滲流模型，沒有考慮多口壓裂水平井同時生產、起伏井筒中的變質量管流等。

1.3 數值模擬法

油田的開發具有不可逆性，數值模擬是油藏開發方案設計中最為重要的參考資料。在解決多相流、多井、復雜縫網模型、非常規儲層生產動態預測等方面優勢明顯。數值模擬法應用網格模型模擬油藏幾何空間形態及流體分布關系，其核心在于網格劃分和差值函數的選取，根據基質與裂縫間滲透率的巨大差異，在對裂縫和基質進行適當的網格離散后，建立壓力和飽和度方程，并進行相應的離散得到網格間的傳導率來模擬地層流體的滲流規律。數值模擬法從算法上進行區分可分為三種（見表2）。

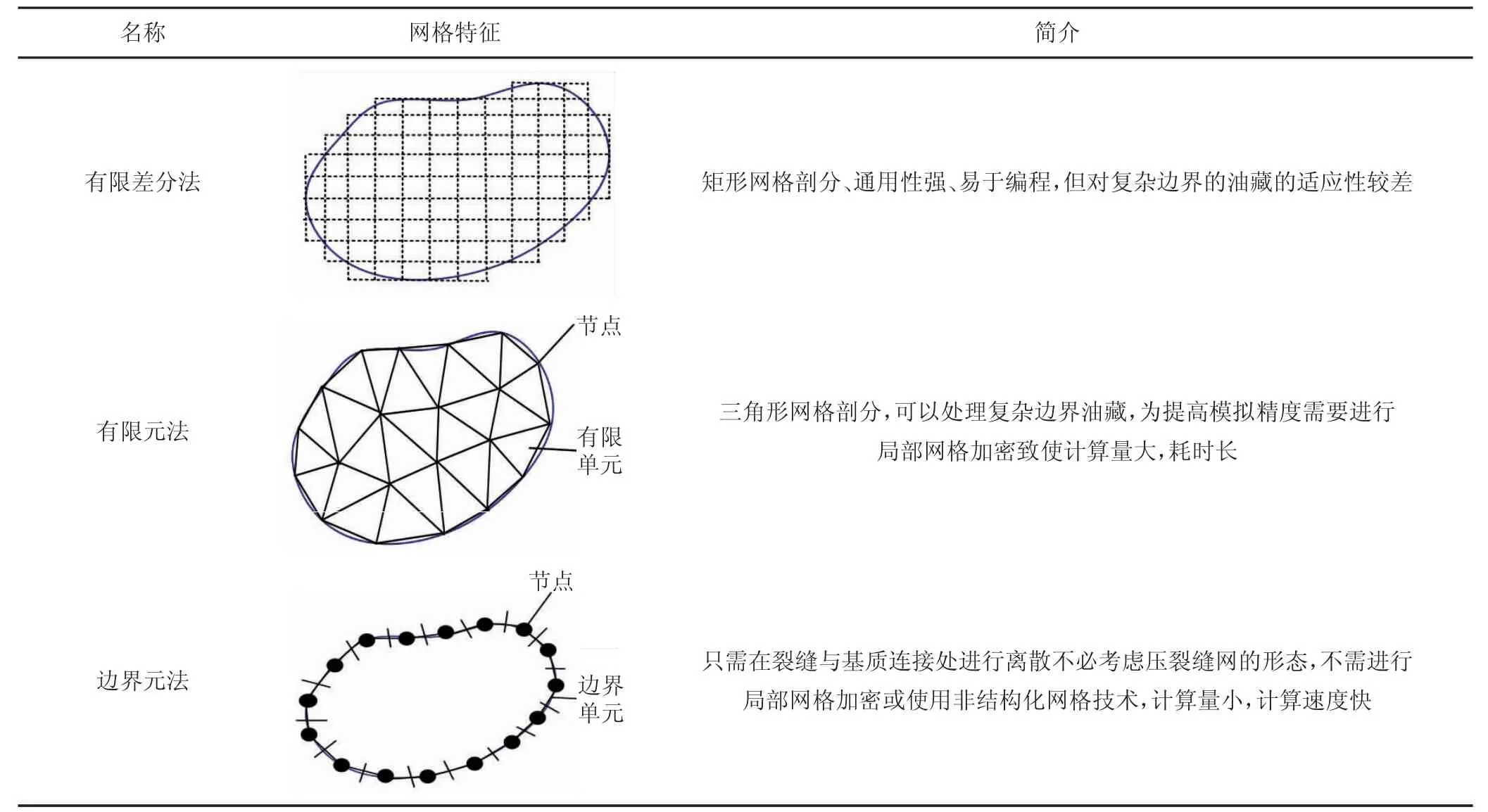
表2 數值模擬法分類

1.3.1 數值模擬法求解步驟 數值模擬法采用時間差分的方法進行油藏開發動態變化過程描述，采用數值解法求解微分方程即數值模擬法可以得到精確模型的近似解，基本步驟：（1）將裂縫和基質進行離散化處理，為了使計算效率提高，需要優化網格數量、大小、形狀等；（2）選取各網格內滲流方程的近似差值函數，為了計算機求解方便，一般選取具有不同次方的多項式；（3）分析簡化得到各網格內滲流方程的特性矩陣方程；（4）將各網格矩陣方程組合形成整個油藏的矩陣方程（包括裂縫和基質），編程求解。

1.3.2 數值模擬法常用數學模型 數值模擬目前常使用的數學模型有：雙重介質模型、等效連續介質模型、離散裂縫網絡模型。雙重介質模型要求基質和裂縫是連續的，所以應用范圍有限；等效連續介質模型主要用于解決地層非均質性對產能的影響；離散裂縫網絡模型計算精度高、適應性強近年來發展迅速。但常規的離散裂縫模型依賴于對井筒及縫網局部進行網格加密處理以實現精準耦合，這就導致計算量的成倍增加。為解決這個問題學者們提出了嵌入式離散裂縫模型Li 和Lee[30]和非結構化網格技術，進一步促進了數值模擬技術的發展。

1.4 有限差分法求解產能模型

有限差分法是一種成熟的數值計算方法，是油藏數值模擬中最早、最常用的方法。主要應用矩形網格對油藏進行離散，為了提高模擬精度需要對裂縫周圍的網格進行加密處理，然后在網格點上選用適當的插值函數，把原問題離散化為差分格式，進而求出數值解，計算方便，易于編程求解。該方法屬于區域型數值模擬方法，需要對整個研究對象進行離散，致使網格數量大、計算速度慢。因此國內外學者的研究重點是優化求解精度及網格數量。

通常數值模擬在求解過程中將裂縫考慮為一個高滲流帶，任嵐等[31]認為假設具有較大的誤差，為此引入了天然差分法求解裂縫與油藏系統單獨滲流時的問題。求解過程中采用隱式壓力-顯式飽和度方法（IMPES），即通過隱式求解地層和裂縫壓力，再通過顯式求解地層和裂縫含水飽和度，從而計算出未來任意時刻壓裂井的產量變化。黃濤等[32]認為傳統的有限差分法基于相鄰網格中心點的壓力值求取網格單元驅替壓力梯度，而低滲透油藏的非均質性極強，在不同區域甚至不同網格單元的啟動壓力梯度不盡相同。基于模擬有限差分法（MFD）采用IMPES 方法（對壓力方程應用MFD 法，對飽和度方程應用有限體積法）對油水兩相流問題進行了模擬，并考慮因儲層的非均質性引起啟動壓力梯度是非線性的問題。

為提高計算效率，國內外學者采用多種方法減少網格數量。Moinfar 等[33]在求解復雜縫網模型中采用嵌入式離散裂縫模型，在對基質進行網格離散后，將壓裂形成的裂縫系統作為單獨的控制體嵌入至油藏網格中，并記錄裂縫與網格之間的相對位置，優點是在劃分網格時不需要考慮油藏內的裂縫形態，對復雜縫網模型較為適用，可大大降低網格數量。由于低滲透油藏在基質、裂縫間的物性參數在數量級上相差很大，具有多尺度特征，由此多尺度數值模擬方法被提出。該方法在網格劃分時先劃分大網格然后將大網格分為有限個小網格，在大網格求解控制方程，小網格上求解局部流動方程獲得多尺度基函數，該方法保持了傳統尺度升級法的計算效率又可降低運算量。張慶福等[34]應用多尺度模擬有限差分法研究嵌入式離散裂縫模型滲流問題，通過在粗網格上求解局部流動問題計算多尺度基函數來捕捉裂縫與基巖間的相互關系，反映單元內的非均質性的同時保證求解精度和求解速度。

1.5 有限元法求解產能模型

有限元法是近年來廣泛使用的數值計算方法，由最初的力學領域擴展到滲流力學。該方法采用三角網格對油藏進行離散，并假設網格內油藏均質，然后選取差值函數，應用Galerkin 計算格式建立有限元方程，并將局部有限單元方程組合成區域內有限元方程組，求解整體有限元方程組，從而得到區域內壓力場、滲流場等特征。相比于標準五點有限差分網格具有線性插值的三角形單元網格更有利于復雜邊界油藏和多相流的模擬[35]。

Langsrud[36]基于有限元法模擬了油氣兩相流動產能模型，開啟了有限元法在油藏數值模擬中的應用。Charles 等[37]對比有限差分法詳細闡述了有限元法的優點：（1）處理復雜邊界問題更加靈活，克服了有限差分法對油藏邊界的限制；（2）網格取向性較弱，可以更好逼近突變面；（3）隱式求解，求解過程更穩定，結果更光滑。這些優點推動了有限元法在油氣藏數值模擬中的應用。

該方法同樣屬于區域型數值模擬方法，為提高計算效率國內外學者應用多種方法簡化網格數量。Karimi-Fard 等[38]采用復合網格離散方法即基質采用三角形離散，裂縫采用線單元離散并進行降維處理，提高了計算速度。在此基礎上萬義釗等[39]考慮了裂縫不等長，不對稱，不等間距等對壓力分布的影響。為進一步優化網格數量，通常使用網格粗化法，但粗化后的大尺度網格不能充分模擬油藏小尺度特征[40]。為此姚軍等[41]基于多尺度混合有限元方法研究了強非均質油藏中的油水兩相滲流問題，建立了油水兩相滲流問題的多尺度混合有限元計算格式，與傳統有限元法相比該方法通過大網格捕獲小尺度特征，在精度與網格數量間得到了平衡，同時也減少了模型求解時間。在此基礎上張娜等[42]對強非均質油藏油水兩相非線性滲流進行研究。

體積壓裂會在地層中產生復雜縫網、為解決開發過程的應力敏感問題，考慮流固耦合效應成為現階段熱門研究方向。徐加祥等[43]對致密油藏中水平井井筒、水力裂縫和天然裂縫的分布進行建模，建立了基質-裂縫-井筒耦合流動模型對壓裂后致密油藏產能進行模擬，并分析不同水力裂縫長度和間距對產能的影響。任龍[44]基于有效應力原理及改造區多重孔隙介質流體流動特征，建立考慮基質、天然裂縫和網絡裂縫系統特征的流固耦合數學模型，進行應力場-滲流場全耦合有限元數值求解。

1.6 邊界元法求解產能模型

邊界元法分為直接和間接邊界元法，在石油工程領域，間接邊界元法多用于解決壓裂過程中裂縫擴展問題，直接邊界元法多用于解決油藏滲流問題的求解。由于有限差分和有限元法應用時需要對整個研究對象進行離散，致使在求解時難以同時兼顧計算速度和精度。而邊界元法只對油藏邊界進行數值離散，優點是：能大幅降低離散單元數量，計算速度快；求解誤差僅來自邊界的離散，對油藏內滲流物理量的求解，采用精確的基本解進行計算。目前應用最廣泛的基本解有：（1）Gringarten 基本解用于解決單重介質油藏滲流問題；（2）Ozkan 基本解用于解決雙重介質油藏滲流問題。

Tiab 等[45]詳細的闡述了邊界元法的優點：（1）劃分的單元格更少且能夠對裂縫進行降維處理；（2）沒有網格取向和數值分散效應；（3）計算速度和精度有很大提高；（4）可以處理復雜邊界油氣藏和邊界條件，靈活性強。

現有文獻主要集中應用于直井和分段壓裂水平井二維滲流模擬。劉青山等[46]認為邊界元法是處理非規則油藏邊界的有效手段，對比有限元法闡述了邊界元法的優點，認為邊界元法在油藏數值模擬和試井領域有廣闊的應用前景。張烈輝等[47]認為邊界元法不僅能求解復雜邊界油藏滲流問題，在非均質油藏滲流方面也具有較好的適用性，并采用復合油藏理論模型建立了縫洞型非均質油藏直井井底壓力分布模型。Idorenyin等[48]將直井等效為二維點源，裂縫為點源沿裂縫幾何形狀的數值積分。詳細的論證了邊界元法不同完井類型（直井、水力壓裂直井、分段壓裂水平井）及邊界條件（封閉、定壓和混合邊界條件）中的應用。Wu 等[49]將油藏分為壓裂波及區（SRV）和未波及區（USRV），在壓裂波及區采用雙孔介質模型及點源函數求解，在未波及區采用單孔介質模型結合運動方程、狀態方程、連續性方程求解，通過對兩個邊界進行線性離散，建立了分段壓裂水平產能模型。

數值模擬法不足：（1）有限差分和有限元法雖已有方法簡化網格離散，但實際油藏尺寸巨大，網格的離散時需兼顧尺寸大小和計算機運算時間。離散后的網格在每個時間步都需要循環計算壓力、網格間的傳導率，致使模型求解時間長，尤其在進行多種方案優化時；（2）目前，邊界元法都是二維滲流模型，不能解決壓裂水平井三維滲流問題；（3）基于網格間傳導率來模擬流體的流動，很難模擬低滲儲層的滲流機理；（4）數值模擬需要提供大量的參數，而油田開發初期部分參數獲取較為困難。

2 結論及發展趨勢

總體來看目前所使用的產能研究方法各有優缺點，國內外學者對此做出了巨大貢獻。而尋找高效、準確的產能預測方法仍是目前致密油氣開發面臨的難題，未來需在下面幾個方面深入研究：

（1）壓裂水平井產能預測最重要的兩點：①滲流模型是產能預測的基礎，占主導地位，但目前還沒有形成統一的滲流模型；②求解方法各異，在對求解精度、速度、復雜度對比時各方法優缺點明顯。不同的學者利用不同的數學模型及求解方法，推導出來的公式有一定差異。因此需要繼續改進并尋找新的滲流模型和求解方法。

（2）壓裂水平井產能預測模型考慮的影響因素越來越全面，圍繞流體在基質、裂縫間的滲流規律不斷有新的理論提出，但目前解析法和半解析法大多考慮單個壓裂水平井、對復雜邊界條件油藏、多口壓裂井間的相互干擾仍需進一步研究；由于致密油藏在壓裂后存在多尺度滲流特征而雙重介質模型對基質與天然微裂縫做“糖塊型”高度簡化的處理無法準確描述多尺度滲流介質的非均質性；現有文獻大多進行單因素的敏感性分析而少見多參數組合優化。

（3）目前數值模擬法對油氣水三相的模擬依然少見，為提高計算效率和精度，未來要在模型建立、網格劃分、算法上進行優化。致密儲層中流體的滲流規律不僅是線性流且往往存在天然裂縫，壓裂后形成的復雜縫網對流體的滲流規律影響很大，如何建立考慮儲層裂縫特征的滲流模型并進行有效模擬是目前研究的重點。