快鏈條模型下落運動的探究
李恩溢 高 博 金偉秋 盛裕杰
(西安交通大學 1理學院,大學物理國家級實驗教學示范中心;2電氣學工程學院,陜西 西安 710049)
在傳統的下落鏈條的力學模型[1]中,認為從一定高度釋放的鏈條的各部分均做自由落體運動,即認為鏈條各部分間不存在拉力。該模型對一般概念下的鏈條有很好的解釋效果,但若拓寬對鏈條的定義,那么只要構造的鏈條足夠特殊則傳統的鏈條模型將不再適用。
目前,國外已有一些研究表明了這一點:R.H.Plaut等人發現一種特殊構造的鏈條,其下落快于自由落體,從而得出下落時鏈條懸空部分存在拉力的結論[2],并稱這類鏈條為快鏈條。Rod Cross等人通過研究不同的幾何形狀的物體落地時的能量耗散,得出了一定條件下剛性桿落地后桿的機械能不守恒的結論[3]。Anoop Grewal等人亦通過理論分析給出了幾種下落速度快于自由落體的鏈條模型[4]。
但目前國外文獻對快鏈條下落過程進行數學描述和計算時,一般采用連續模型對整段鏈條的下落過程進行描述,即認為快鏈條在下落過程中速度是連續變化的,而實際上,快鏈條在下落過程中運動的模式是反復切換的,速度變化曲線也存在跳躍間斷。因此,為補充已有研究的不足,本文將針對一種典型結構的快鏈條,對其下落過程的各個階段展開分析,以得出描述快鏈條下落的一般方程,并通過實驗驗證該模型的合理性。
1 快鏈條下落過程的定性分析
本節定性分析快鏈條的下落過程,通過證明快鏈條落地后存在局部的速度突增,說明鏈條下落時,連接繩將繃緊而產生拉力,從而也就說明了快鏈條下落時速度快于同高度釋放的自由落體運動的速度。
本文研究的快鏈條是一根由若干與水平面有一定角度的木棍以及兩條連接繩構成的鏈條,如圖1所示。

圖1 快鏈條示意圖
由于快鏈條結構的特殊性,快鏈條在以一定速度撞擊桌面后,鏈條會有一個速度的突增,使得懸空部分鏈條的連接繩拉緊產生拉力,從而使得懸空部分以大于重力加速度的加速度下落。下面證明這一點。

圖2 木棍落地前以及落地瞬間的受力分析圖
如圖2所示,先取快鏈條最下端的木棍進行分析,假設木棍與地面的碰撞是完全非彈性的,在該木棍與地面碰撞的極短的時間內,左端的速度突變為零,木棍開始做繞左端點A的定軸轉動運動。由于在極短的時間內可認為木棍受到外力的沖量矩為零,則由角動量定理[5]可得:
其中,V(x)為鏈條與地面剛要碰撞之前鏈條的速度;θ0為木棍與水平面的初始夾角;x為沿桿方向的積分變量;m為單根木棍的質量;l為木棍的長度;ω為鏈條與地面碰撞后,開始繞A點轉動瞬間木棍繞A點轉動的角速度。
由于在與地面碰撞之前,木棍上各點的速度均相等,可以都設為Vb,因此角動量守恒的等式化為
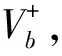
(1)

圖3 木棍落地瞬間鏈條的速度變化
考慮到連接繩不可伸長,則底端木棍右端點速度的豎直分量和懸空部分的速度將很快達到同速,顯然該速度將大于懸空部分原來的下落速度,小于底端木棍右端點原來速度的豎直分量,如圖3(b)所示。下面推導該速度。
該過程所用的時間極短,則重力產生的沖量矩可以忽略,所以可由角動量守恒定理得到如下式:
其中,n為懸空部分的木棍數量;V+為底端木棍和上方鏈條達到同速后的共同速度。求解上式得:
(2)
上式表明了在木棍初始傾角滿足條件的情況下,每當一根木棍落地懸空部分的鏈條都會產生一次速度突增,且原速度越大,速度突增的量值也就越大。
為驗證上述理論推導得出的結論,本文選用木棍和細繩制作了快鏈條,并對其下落過程進行了錄像,從錄像中截取到了如圖4所示的快鏈條下落瞬間的圖像。

圖4 快鏈條下落過程中某一時刻的圖像
從圖4中的標記處可以看出,最底端木棍的一端碰撞地面時,該木棍的另一端與上方未落地鏈條之間的連接繩處于繃緊的狀態。從而驗證了上文推導出的因底端木棍速度突增而使得底端木棍與上方未落地鏈條之間連接繩繃緊的結論。
2 快鏈條下落過程的定量描述
基于上節的定性分析和速度突增的結論,本節建立描述快鏈條下落過程的微分方程。
底端鏈條與地面接觸并開始做定軸轉動的某時刻的鏈條如圖5所示,設在該時刻未落地的懸空部分有n根木棍,底端木棍此時與水平面的夾角為θ。
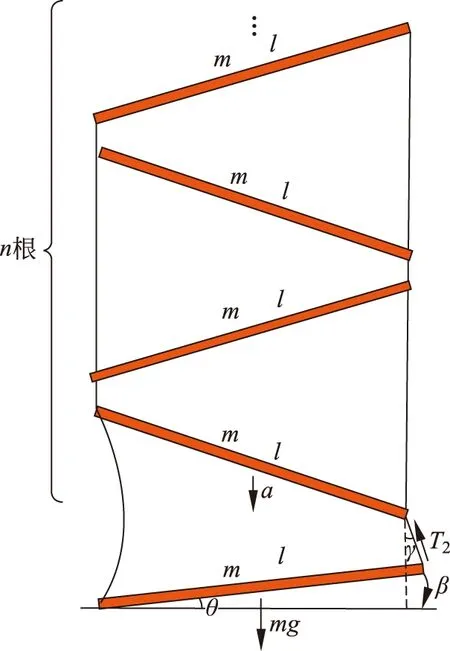
圖5 快鏈條受力分析圖
由上節分析知T2>0,所以對最下端的木棍由轉動定理得:
對懸空部分的鏈條由牛頓第二定理得:
nmg+T2cosγ=nma
由于連接繩拉直所以沿繩方向上上下兩部分的加速度必相等有
acosγ=lβcos(γ-θ)
由上3個式子得加速度為
若每兩根鏈條之間的距離很短,則可認為γ=0,上式化簡為
(3)
可以看出要使加速度大于重力加速度g則需滿足:
化簡得:
該式表明了快鏈條下落快于自由落體的臨界角條件為θ<35.26°,這一結論與第1節的定性分析結果完全一致。
在此基礎上,求解任意時刻快鏈條的位置。考慮到上方木棍數目n是一個離散量,要得到鏈條下落過程中鏈條下落距離與時間的關系,首先需要對n的不同取值進行分段求解,且應考慮到每根木棍落地時的速度突增。
設快鏈條底端木棍碰撞地面的瞬間鏈條的初速度為Vb,木棍與水平面的初始傾角為θ0,懸空部分的木棍數為n。當底端木棍轉過一定角度后,底端木棍與水平面的夾角為θ,底端木棍未落地的一端離地面的豎直距離為X,如圖6所示。

圖6 快鏈求解示意圖
由幾何關系有
將上述兩式代入式(3),則可以得到鏈條下落過程中底端木棍未落地端的豎直高度X關于時間t的微分方程:
結合速度突變表達式(2),可以得到確定底端木棍豎直高度X與時間t的微分方程和定解條件為
(4)
該式表明在初始角度滿足條件的情況下,當某一節木棍以Vb的初速度落地時,上方的鏈條瞬間產生速度突增和加速度的突增,并在底端木棍與水平方向的夾角減為零之前,始終按上述微分方程的形式保持著大于重力加速度的加速度,這也間接證明了快鏈條下落時,鏈條的連接繩間存在拉力。該現象的本質是底端木棍在撞擊地面后動能沒有完全損失,而轉移了一部分能量到上方未落地的鏈條。
需要指出的是,上述微分方程和定解條件的求解結果是,快鏈條的一節木棍落地過程中,快鏈條底端高度隨時間的變化。當求解整個快鏈條的下落過程時,對木棍撞擊地面的過程采用式(4)的微分方程,且由于每節木棍落地時其上方懸空的木棍數目不同,因此每次求解時應改變方程中的n值;對木棍與木棍銜接部分,由于沒有木棍落地,繩中沒有拉力,應按自由落體求解;同時,應考慮到快鏈條每段自由落體運動的末速度按速度突增式(2)處理后,才是下一段微分方程的初速度。
綜上所述,可不失一般性的將快鏈條的下落過程按如下過程理解:鏈條先做自由落體運動,自由落地運動的末速度即為下一節木棍落地前瞬間鏈條的速度,木棍與地面接觸后瞬間鏈條速度按式(2)規律突增,之后鏈條按式(4)的微分方程的規律運動,當木棍繞端點轉動至傾角為零后,快鏈條又開始做自由落體運動,如此反復,直到鏈條落完。
3 數值求解及實驗
為驗證本文模型的合理性,本節將使用自制的快鏈條進行實驗并通過高速攝影機和Tracker軟件對快鏈條的下落過程進行記錄和測量,并將理論計算結果與實驗測得結果進行比較。
為初步了解快鏈條的下落過程,基于本文第1節和第2節所得結論,本文首先針對總木棍數為15根,木棍長度為17.5cm,初始傾角為15°,木棍間間距為1cm的快鏈條進行數值求解。其中對微分方程的求解借助了Matlab軟件的ode45指令。數值求解結果如圖8所示。
從圖7可以看出,由于快鏈條加速度始終大于等于重力加速,因此其位移和速度也始終大于或等于自由落體,從位移圖像上看,快鏈條與自由落體的位移差隨時間增加逐步增大;從速度圖像上看,快鏈條的速度始終增長的比自由落體快,且可以明顯看出由于每根木棍落地時的速度突變;從加速度圖像上看,每根木棍落地瞬間鏈條的加速度瞬間突增,超過重力加速度,且在木棍與水平面夾角逐漸減小的過程中木棍的加速的不斷增大,但到夾角完全等于零后,加速度又變回重力加速度,并在下一根木棍落地之前做自由落體運動,加速度保持重力加速度不變。
為驗證本文模型的合理性,本文針對具有不同尺寸參數的快鏈條進行了實驗,快鏈條的結構參數包括木棍間距d,棍長l,初始傾角θ0,因為確定了這3個參數,即可確定快鏈條的尺寸結構,3個參數的示意圖如圖8所示。
同時,由于鏈條速度突增的量值與原速度有較大的關系,因此本實驗分別以木棍間距d,的棍長l,初始傾角θ0以及初始速度V0為參數進行實驗,通過高速攝影機拍攝快鏈條的下落過程,將慢速回放的錄像導入Tracker軟件,再選定快鏈條頂端的一點進行追蹤,并記錄該點位置隨時間的變化,即可得出快鏈條下落過程中位置隨時間的變化,實驗結果如圖9到圖13所示。其中實驗組2到實驗組5分別與實驗組1形成改變不同參數的對照。
實驗組1:木棍數15根,棍長101.63mm,木棍間距8.26mm,初始傾角25.24°,初速度0m/s。
實驗組2:木棍數15根,棍長101.63mm,木棍間距16.03mm,初始傾角25.24°,初速度0m/s。

圖7 快鏈條位移,速度,加速度圖像(a) 位移圖像; (b) 速度圖像; (c) 加速度圖像
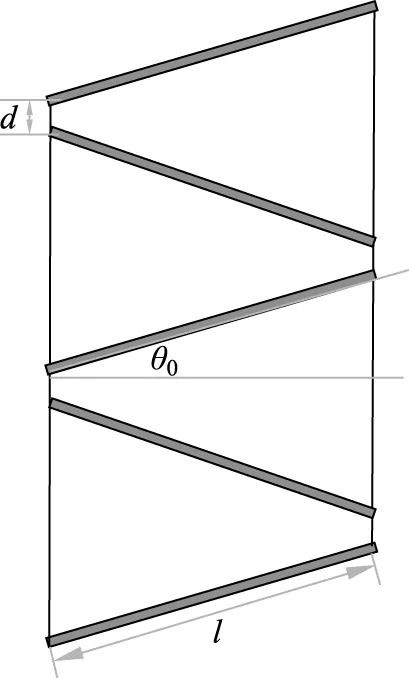
圖8 快鏈條尺寸參數示意圖
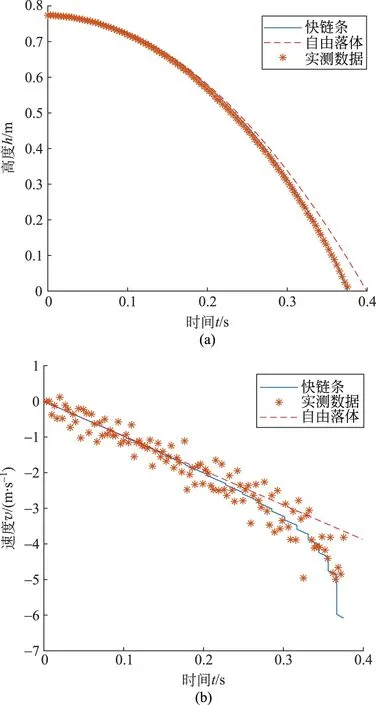
圖9 實驗組1的求解結果與實測數據對比圖(a) 高度與時間的關系圖; (b) 速度與時間的關系圖
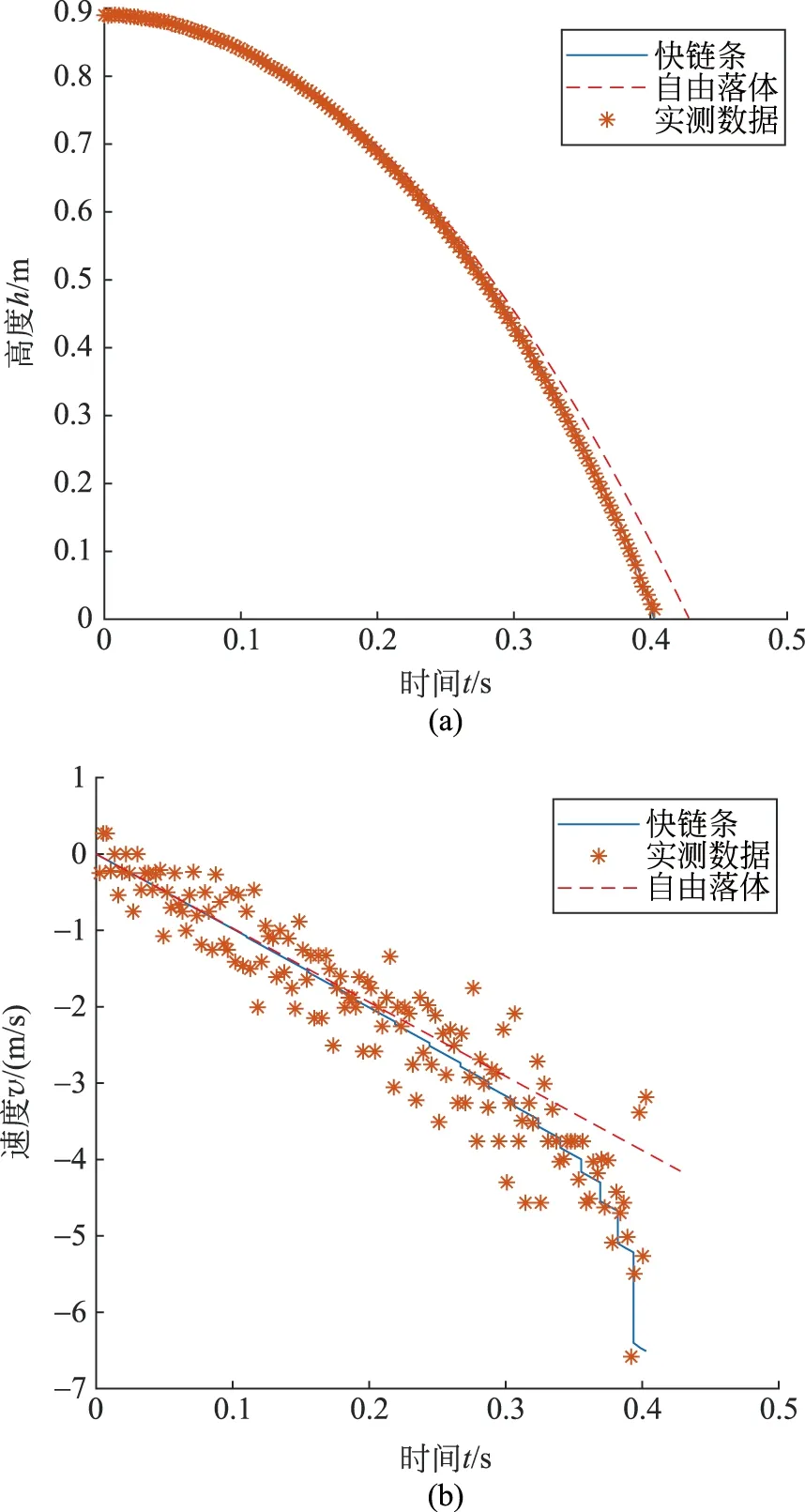
圖10 實驗組2的求解結果與實測數據對比圖(a) 高度與時間的關系圖; (b) 速度與時間的關系圖
實驗組3:棍數15根,棍長101.63mm,木棍間距8.26mm,初始傾角32.83°,初速度0m/s。
實驗組4:棍數15根,棍長201.67mm,木棍間距8.26mm,初始傾角25.24°,初速度0m/s。
實驗組5:棍數15根,棍長101.63mm,木棍間距8.26mm,初始傾角25.24°,初速度-0.65m/s。
1) 實驗組1與實驗組2形成以木棍間距為變量的對照試驗
由理論分析可知,在木棍與木棍銜接部分由于沒有木棍落地,加速度為重力加速度,不及有木棍落地時的加速度大。所以,棍間的距增大會導致鏈條在下落過程中有更多的時間處于自由落體,因此在下落了相同距離的情況下,速度小于棍間距較小的鏈條。實驗結果也符合上述的分析。
2) 實驗組1與實驗組3形成以初始傾角為變量的對照試驗
由實驗結果可以看出,當初始傾角增大,快鏈條的位移圖像更加接近自由落體,說明了初始傾角的增大會使得快鏈條下落變慢。對此可做如下解釋。
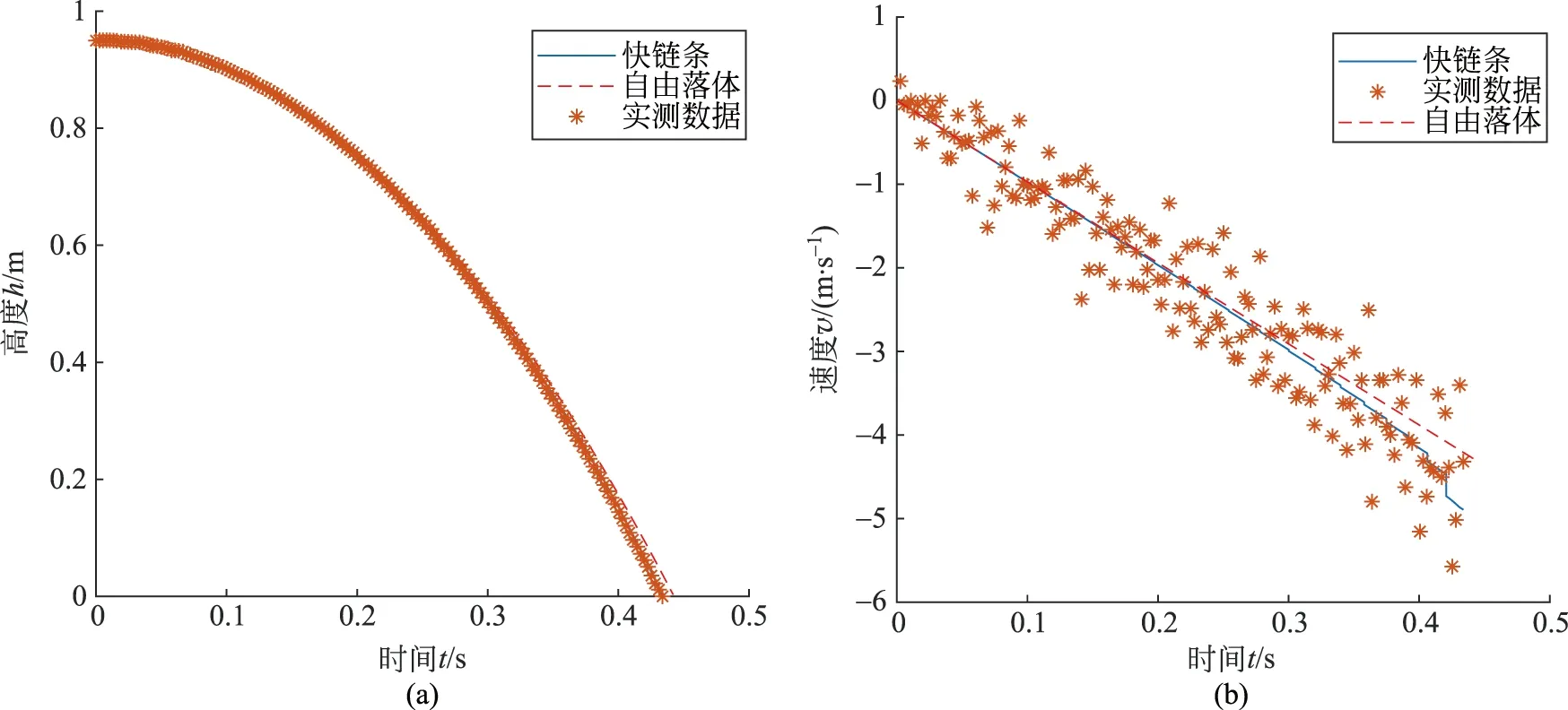
圖11 實驗組3的求解結果與實測數據對比圖(a) 高度與時間的關系圖; (b) 速度與時間的關系圖
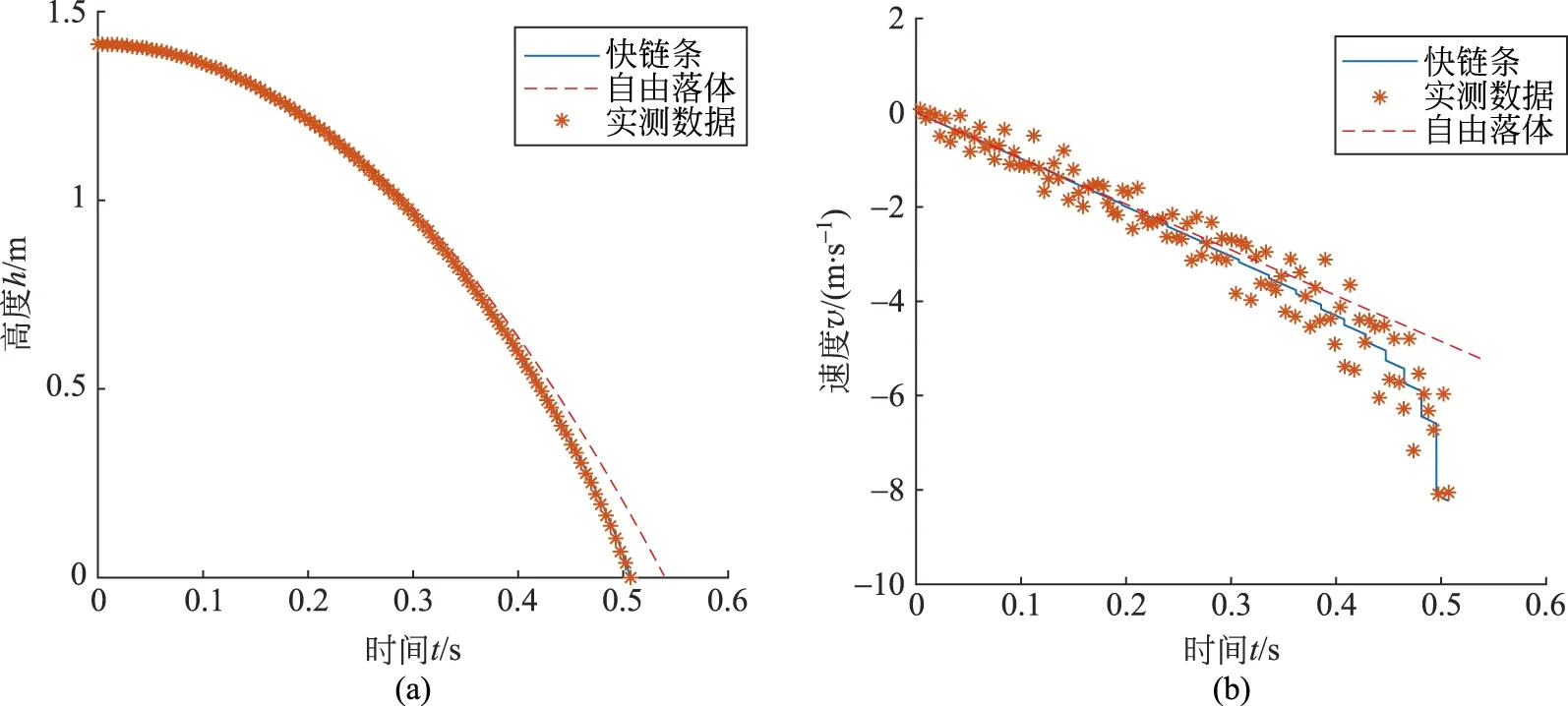
圖12 實驗組4的求解結果與實測數據對比圖(a) 高度與時間的關系圖; (b) 速度與時間的關系圖
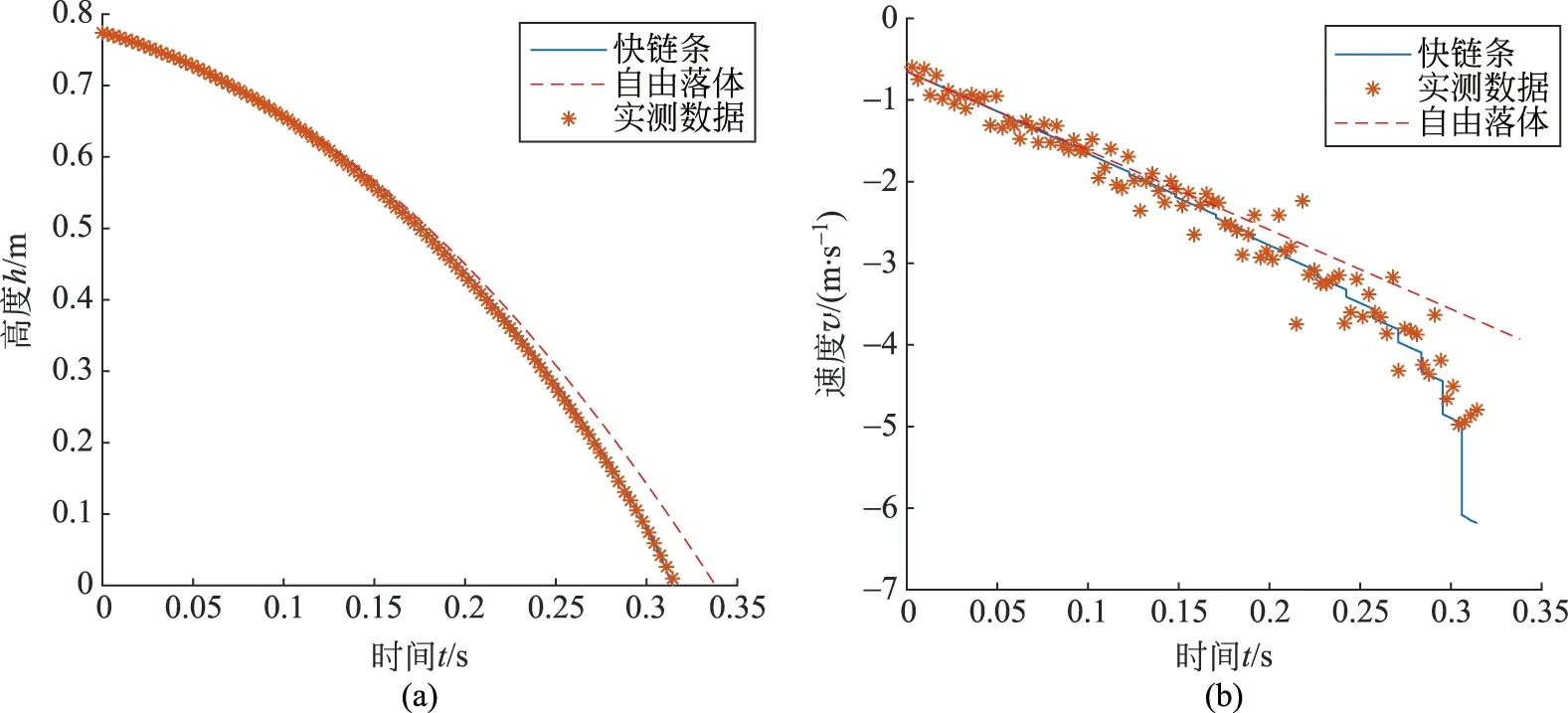
圖13 實驗組5的求解結果與實測數據對比圖(a) 高度與時間的關系圖; (b) 速度與時間的關系圖
由第2節推導出的加速度公式:

3) 實驗組1與實驗組4形成以棍長為變量的對照試驗
棍長l的增長帶來影響,主要體現在兩個方面。一方面是,l增大時,會使得每節木棍落地后,木棍未落地一端端點距地面距離lsinθ0增大。另一方面是,由上述加速度的計算公式可以看出,在高度X取值相同的情況下l越大則cos2θ的值越大,從而加速度a越大。
4) 實驗組1與實驗組5形成以初速度為變量的對照試驗
由于在其他參數不變的情況下,每節鏈條落體時的突增后的速度與原速度成正比,如第1節所推導的公式:
則初速度的增大會導致快鏈條的速度與自由落體運動速度的差值更快的增大。實驗結果也符合上述分析。
4 結論
由上述實驗以及理論計算結果,可以明顯看出快鏈條的理論計算曲線相比一般自由落體曲線,可以更好地擬合實測數據點,這很好地說明了在初始角度滿足要求的情況下,快鏈條在下落過程中始終快于自由落體,從而也就間接地說明了快鏈條下落過程中,鏈條的連接繩存在拉力。同時實驗及理論結果也說明了,快鏈條的下落過程主要受以下參數的影響,分別為棍長,木棍間距,初始傾角以及初速度。
快鏈條作為一種結構特殊的鏈條模型,是對傳統鏈條模型的補充和修正。且由于結構特殊,相比普通鏈條,快鏈條與剛性平面碰撞后,快鏈條機械能的損耗小于普通鏈條,因此,快鏈條的鏈條結構對于如何通過改良物體結構,減少物體在碰撞過程中的動能損耗具有一定啟發作用。該實驗也可作為中學、大學實驗中的運動學趣味實驗進行演示,以提高學生的學習興趣和創新思維。

