基于共因失效貝葉斯網絡的魚雷現場使用可靠性評估

王新鵬，張靜遠，王 鵬，徐振烊

(海軍工程大學兵器工程學院，武漢 430033)

現代魚雷是復雜的水下精確制導武器，組成魚雷的部件種類繁多，包含電子、機械、機電、橡膠等[1]。魚雷從出廠到壽命終結分貯存、裝載和實航3種典型的狀態，在服役過程中，魚雷會經歷多次的貯存、裝載和實航過程[2]。對于部件而言，不同的狀態條件下環境不同，部件承受的應力不同，造成部件的故障規律不同，且部件之前經歷的狀態也會對其可靠性變化規律產生影響。目前在對魚雷或部件進行可靠性分析時，單純考慮魚雷在某種狀態下的可靠性規律，沒有結合魚雷現場使用實際[3-4]。例現場使用條件下，魚雷貯存一段時間后經技術準備檢查完好后，轉入裝載后的可靠性與單純在轉載狀態的可靠性相比，雖均是從1開始變化，但變化規律發生變化。因此，有必要研究實際現場使用條件下魚雷系統可靠性。

本研究按照由部件到系統的思路，在已知部件單一狀態故障規律的基礎上，研究現場使用條件下部件的可靠性變化規律。在此基礎上，建立基于傳統貝葉斯網絡和考慮共因失效的貝葉斯網絡的魚雷系統可靠性評估模型，分別利用兩種分析方法對系統故障概率、部件重要度和后驗概率，并進行對比分析。該方法為分析魚雷系統現場使用的可靠性變化規律和確定系統的薄弱環節提供指導。

1 經歷多個狀態的部件可靠性分析

1.1 條件可靠度

條件可靠度的定義：當故障時間為T的一個產品單元在t=0時開始工作，一直正常工作到時間t，那么該產品單元再正常工作x時間的可靠度為[5]

R(x|t)=Pr(T>x+t|T>t)=

(1)

對于魚雷裝備而言，設某類型部件在貯存狀態的可靠性變化規律為R1(t)，在裝載狀態的可靠性變化規律為R2(t)，在實航狀態的可靠性變化規律為R3(t)。

根據條件可靠度的定義，假定貯存時間t1后，經技術準備檢查完好，魚雷轉入裝載狀態，則該部件在裝載狀態的可靠性變化規律變為

(2)

其中，R2(t20)=R1(t1)。

假定貯存t1時間后，經技術準備轉入裝載狀態，裝載t2時間后，經檢查魚雷功能正常，轉入實航發射狀態，其在實航狀態下的可靠性變化規律變為

(3)

以此類推，可以計算任意時刻在任意狀態的部件的可靠性變化規律。

特別地，當部件可靠性變化規律為指數分布時，設在貯存狀態下滿足R1(t)=e-λ1t，在裝載狀態下滿足R2(t)=e-λ2t，在實航狀態下滿足R3(t)=e-λ3t。貯存時間t1后經技術準備轉入裝載，則在裝載狀態下的可靠性變化規律為

(4)

貯存時間t1后，經技術準備后裝載時間t2，功能正常，轉入實航狀態，其在實航狀態下的可靠性變化規律變為

(5)

由此可見，可靠性變化規律服從指數分布的部件在某種狀態下的可靠性變化規律沒有發生變化，與之前的經歷無關。

1.2 參數估計

對于故障分布函數F(t)為威布爾分布和對數正態分布的部件，需根據式(1)進行計算，然后利用最小二乘法對其分布進行參數估計。

1) 威布爾分布的參數估計

威布爾分布的分布函數為

F(t)=1-e-tm/t0,m>0,t0>0,t≥0

(6)

(7)

2) 對數正態分布的參數估計

對數正態分布的分布函數可寫為

式中：Φ(Z)指標準正態分布的分布函數，有

(8)

令x=lgt，則x=σZ+μ等同于y=b0+b1x。因此，對于Z和x的一組數據，同樣可以用最小二乘法計算回歸系數b0,b1和相關系數r，并得到對數正態分布參數的估計為

(9)

求得經歷多個狀態后的部件故障分布函數后，利用考慮共因失效的貝葉斯網絡模型對魚雷系統的可靠性進行分析。

2 考慮共因失效的貝葉斯網絡模型

共因失效(Common Cause Failure，CCF)是一種源于某種共因的多重故障，這種故障普遍存在于工程系統中，增大了系統各故障模式的聯合故障概率，降低了冗余系統可用度，若忽略系統部件之間的相關性，假設部件故障相互獨立的條件下對系統進行可靠性評估容易造成一定的誤差[6-7]。目前用于處理共因失效的模型主要有α因子模型、β因子模型、MGL模型等[8-10]。

貝葉斯網絡是一個有向無環圖(directed acyclic graph,DAG),它由代表變量的節點及連接這些節點的有向邊構成[11-13]。貝葉斯網絡不但可以實現正向推理,由先驗概率推導出后驗概率,即由原因導出結果,還可利用公式由后驗概率推導出先驗概率,即由結果導出原因。

1) 傳統的貝葉斯網絡模型

設系統由部件X1,X2,…,Xn組成，建立傳統的貝葉斯網絡模型如圖1所示。

圖1 傳統貝葉斯網絡模型示意圖

計算不考慮共因失效情況下系統的故障概率為

(10)

計算系統故障條件下，各部件故障的后驗概率為

(11)

利用貝葉斯網絡計算各部件的重要度為

概率重要度：

(12)

結構重要度：

(13)

關鍵重要度：

(14)

2) 考慮共因失效的貝葉斯網絡模型

建立考慮共因失效的貝葉斯網絡模型的關鍵時將系統中的共因失效部件的故障率分為獨立故障率和相關故障率每個部件串聯了一個共因失效部件，此共因失效部件的故障率為兩個獨立部件的共因失效概率。如圖2所示，設系統由部件X1,X2,…,Xn組成，共因失效部件為M，每個獨立故障部件和共因失效部件的子節點為M1,M2,…,Mn。

考慮共因失效的貝葉斯網絡的系統故障概率計算公式為

(15)

考慮共因失效的部件后驗概率及部件的重要度計算，可先求得系統的故障概率，再代入相關公式進行計算。

圖2 考慮共因失效的貝葉斯網絡模型示意圖

目前處理共因失效的模型較多，采用β因子模型只需確定一個參數，且不存在數據丟失的問題，故本文采用β因子模型對共因失效事件進行定量分析。假設某部件的總故障率Qt可以分解成獨立概率QI和相關概率Qc，通過引入參數β表示相關故障率與組件總故障率的比值：

Qt=QI+Qc

(16)

(17)

對以往共因失效數據的分析研究，得出β因子的一般取值范圍為0～0.25(0表示不發生共因失效)，硬件β的因子取值一般為0.01～0.1。在相關部件對外部條件相對敏感的情況下，β的因子取值一般相對較大。此外，為了簡化計算分析，當考慮共因失效對系統的影響時，認為共因失效對系統影響是決定性的，即當部件受到共因失效的影響時，部件完全故障。

3 實例分析

假定某魚雷系統有2個分系統組成，每個分系統由2個關鍵部件組成，各部件在貯存和裝載狀態下的故障分布函數和參數，如表1所示。

3.1 經歷貯存狀態后的部件的裝載可靠性分析

該型魚雷出廠后，在倉庫經歷1年的貯存后，經技術準備的環節，檢查完好，轉入裝載狀態，研究各個部件在裝載狀態的可靠性的變化曲線。

利用1.1節和1.2節相關內容進行計算和參數估計，得到經歷貯存后，在裝載條件下部件故障分布函數參數如表2所示。

表1 貯存和裝載狀態下關鍵部件的故障分布函數和參數

表2 經歷貯存狀態后部件在裝載狀態的故障分布

部件X1和X2因故障分布為指數分布，裝載狀態下可靠度函數不變，部件X3和X4的可靠度變化曲線分別如圖3和圖4所示。

圖3 部件X3可靠度變化曲線

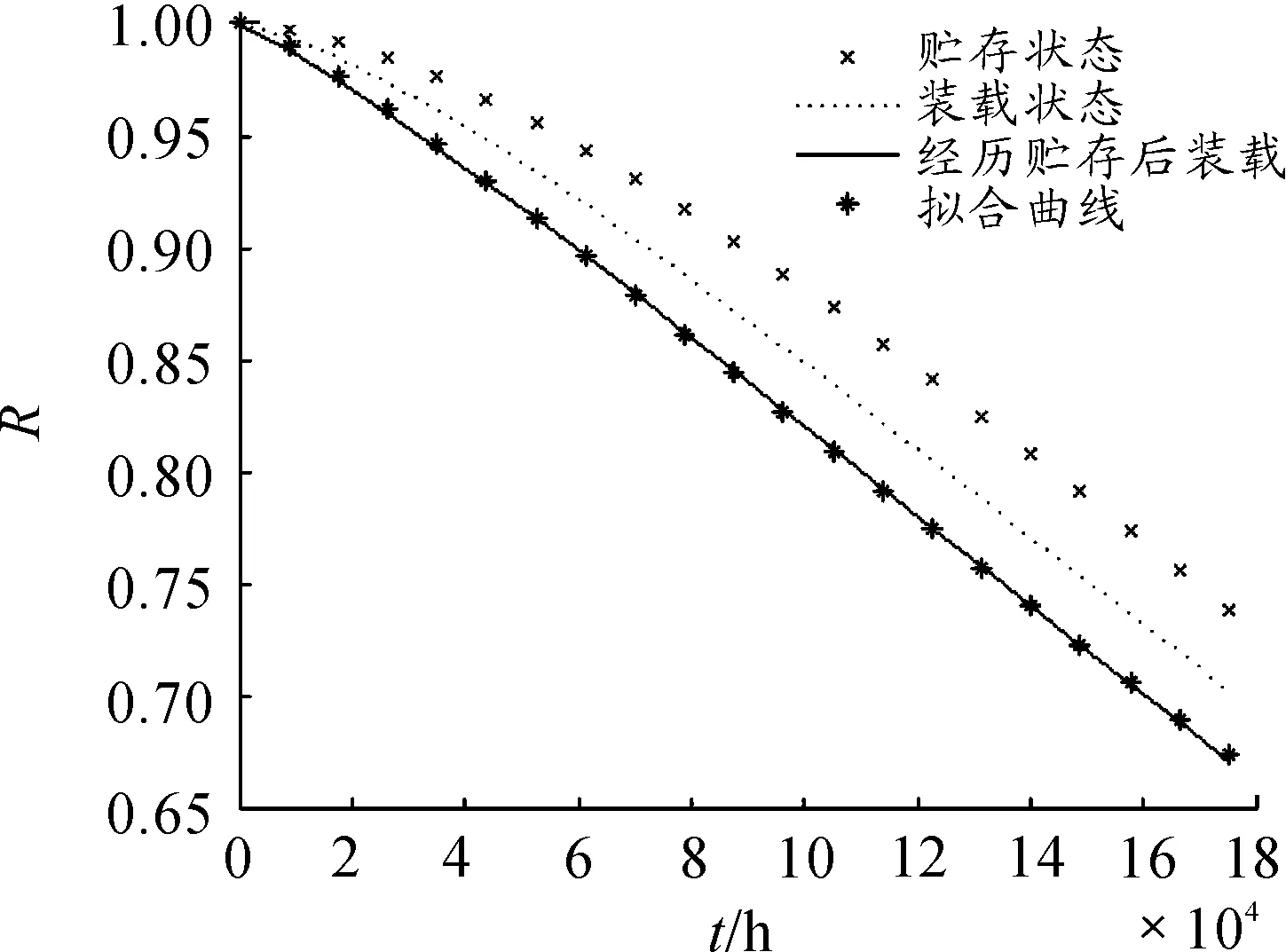
圖4 部件X4可靠度變化曲線

從其中可以看出，部件X3和X4經歷貯存狀態，經技術準備轉入裝載后，裝載可靠度較單純在裝載狀態的可靠度有所下降。

3.2 考慮共因失效的魚雷系統可靠性分析

在裝載狀態下，魚雷系統中任一部件故障，則認為魚雷系統出現故障。因此，任一分系統下的兩個部件邏輯關系為或門，分系統之間邏輯關系為或門。部件之間是否存在共因失效可以根據故障數據等方法進行分析，假定部件X1和部件X2存在共因失效，建立傳統貝葉斯網絡模型和考慮共因失效的魚雷系統貝葉斯網絡模型，如圖5和圖6所示。

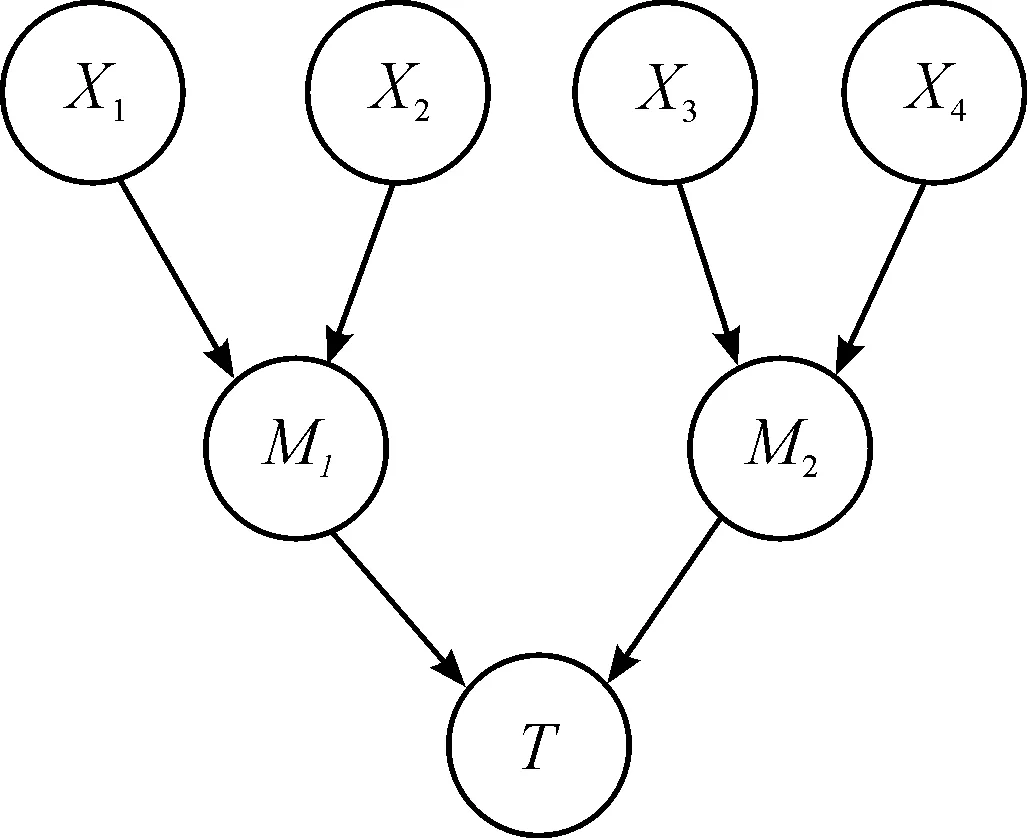
圖5 傳統的貝葉斯網絡模型示意圖

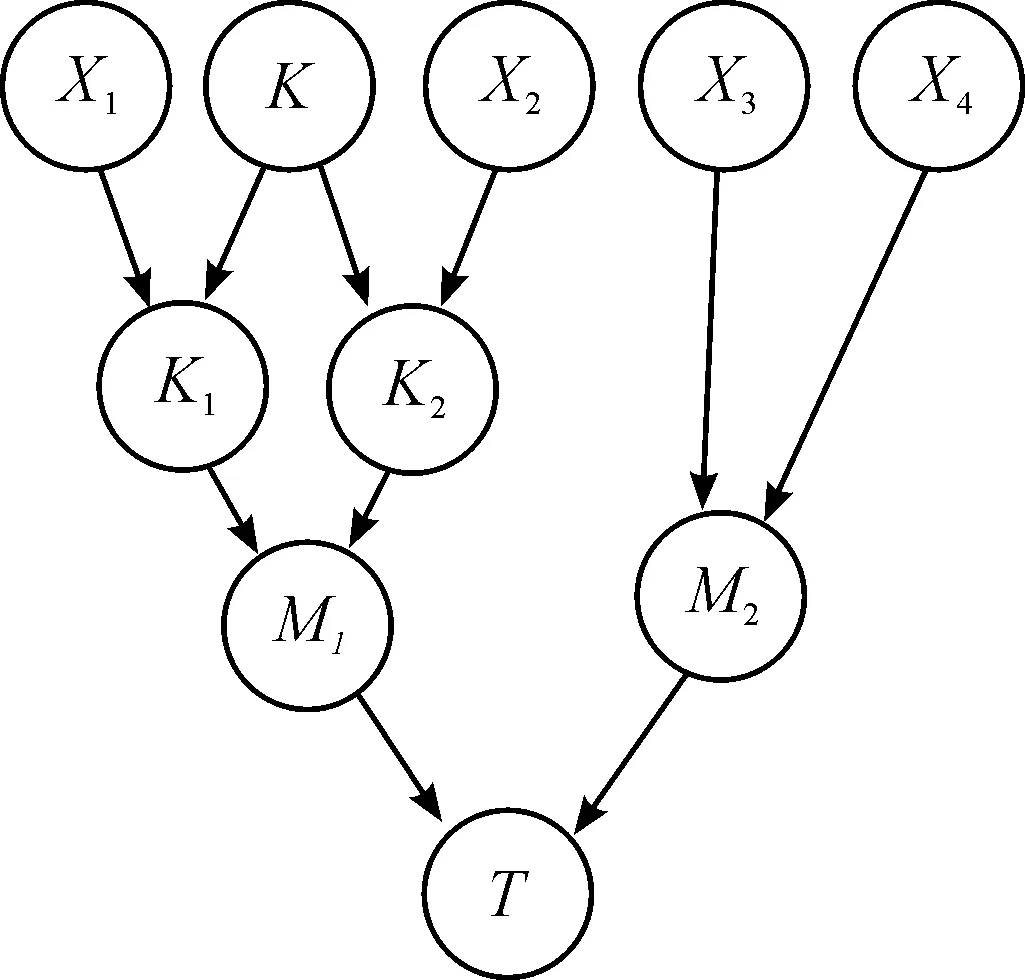
圖6 考慮共因失效的系統貝葉斯網絡模型示意圖

部件X1和X2的故障分布均為指數分布，故障率分別為λ1=5.32×10-6/h和λ2=4.93×10-6/h。采用整合部分法(unified partial method,UPM)對β因子的值進行估計，取部件X1和X2的共因失效因子為0.1。根據β因子模型，部件的獨立故障率λ和共因失效率λm的關系為

β=λm/λ

(18)

根據式(18)可以計算出部件X1和X2的共因失效率分別為λ1m=0.532×10-6/h和λ2m= 0.493×10-6/h。因此，部件X1和X2的共因失效率為λm=0.493×10-6/h。

利用傳統的貝葉斯網絡和考慮共因失效的貝葉斯網絡分析方法對魚雷系統裝載1年時的可靠性進行分析。

1) 系統故障概率

傳統貝葉斯網絡分析方法和考慮共因失效的貝葉斯網絡分析方法計算魚雷系統的故障概率如表3所示。

表3 魚雷系統故障概率

從表3中數據可以看出，在考慮共因失效的情況下，系統的故障概率高于傳統的不考慮共因失效情況下的故障概率。這是因為在考慮共因失效的情況下，共因失效因子會對系統產生影響，因此，考慮共因失效情況下，系統的故障概率計算結果更加精確，更加符合實際。

2) 部件的重要度計算

利用傳統貝葉斯網絡分析方法和考慮共因失效的貝葉斯網絡分析方法對魚雷系統的部件的概率重要度和關鍵重要度進行計算，如表4和表5所示。

表4 部件的概率重要度

表5 部件的關鍵重要度

由于裝載狀態下，任意部件故障都會導致魚雷系統故障，所以4個部件的結構重要度是相同的，本節沒有進行特別計算。從其中可以看出，傳統的貝葉斯網絡分析方法計算的概率重要度和關鍵重要度要比考慮共因失效情況下的貝葉斯網絡分析方法計算的結果要大。部件的故障概率越大，計算得到該部件的概率重要度和關鍵重要度也越大。

3) 部件故障的后驗概率

利用貝葉斯網絡的反向推理，計算魚雷系統故障的條件下，各部件故障的后驗概率，結果如表6所示。

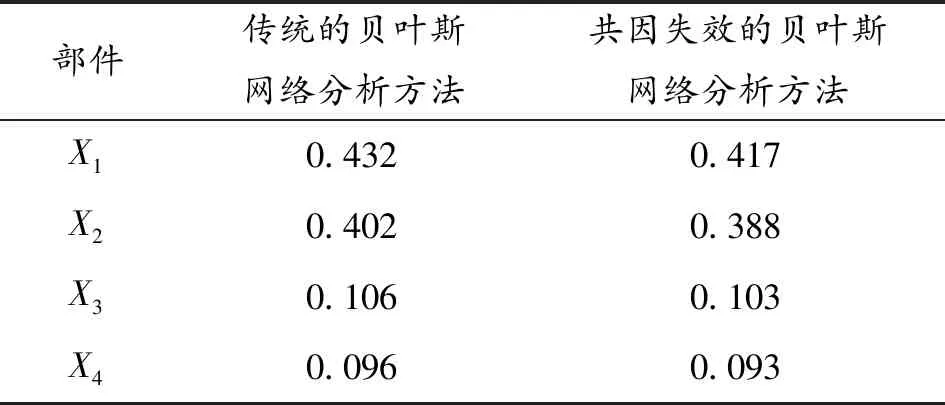
表6 部件故障的后驗概率

從表6中可以看出，假定系統故障的條件下傳統貝葉斯網絡分析方法計算的部件故障后驗概率值要大于共因失效的貝葉斯網絡分析方法計算的結果。

綜上，比較傳統貝葉斯網絡分析方法和共因失效的貝葉斯網絡分析方法的計算結果，可以看出：

1) 考慮共因失效的貝葉斯網絡分析方法的魚雷系統的故障概率升高了，部件的概率重要度、關鍵重要度和后驗概率降低了；

2) 部件X4的先驗概率、概率重要度、關鍵重要度及假設系統故障條件下的后驗概率相對來說都是最大的，因此可以判斷部件X4是控制系統相對的薄弱環節。

3) 不考慮系統存在共因失效的影響時，會對系統故障概率的計算結果造成誤差，共因失效的貝葉斯網絡分析方法更符合實際情況，具有更高的計算精度。

圖7表示裝載1年時，魚雷系統故障概率隨β因子值的變化而發生變化的情況。從中可以看出，隨著β因子值的增加，魚雷系統的故障概率呈線性增加。因此可以通過改善共因失效因子β的值來降低系統故障概率。

圖7 β因子值與系統故障概率的關系曲線

4 結論

利用考慮共因失效的貝葉斯網絡分析方法可為魚雷系統可靠性設計、狀態維修和故障診斷提供依據，對求解可靠度等指標、發現潛在隱患和薄弱環節，保證系統的運行安全可靠、避免重大事故發生都具有重要的現實意義。