三維Lieblattice模型的能譜結構

劉書言, 于 靜

(遼寧石油化工大學 理學院, 遼寧 撫順 113001)

在凝聚態物理中,材料的宏觀性質與能帶結構有著密不可分的聯系。根據能帶的填充情況,可以將材料劃分為金屬、半導體和絕緣體[1]。隨著對拓撲物態研究的不斷深入,傳統意義上的能帶理論也被極大地拓展,材料的類別被更詳細地劃分。對拓撲物態的研究已成為凝聚態物理學的重點研究方向之一[2]。Lieb lattice模型不僅具有獨特的簡立方對稱結構,在該模型上可以研究量子霍爾效應[3]和量子反常霍爾效應[4],探究拓撲量子相變所需要的條件還具有其他有趣的性質,如非線性衍射、超導躍遷、自旋漲落與超導配對對稱性[5],磁霍爾效應,磁相圖,分數階chern絕緣子[6]等。近年來,已有多個研究團隊對二維(2D)Lieb lattice模型進行深入研究并取得突破性的進展[7-10],但對三維(3D)的研究還處于初級階段。本文研究了3D模型的能譜特征,并在模型上施加自旋軌道耦合作用,分析了對其能譜產生的影響。

1 3D Lieb lattice模型

2D Lieb lattice模型是一種具有各向同性最近鄰躍遷的正方邊心格子[11]。由于其特殊的拓撲結構和物理性質在近些年得到了研究者們廣泛的關注與研究。2D Lieb lattice模型上的每個原胞中都含有3個不同的原子,其幾何結構如圖1(a)所示,3個原子分別標記為A,B,C,2個最近鄰格點間的晶格常數為a[12]。在Lieb lattice模型上可以實現對拓撲物質狀態的研究。其能譜是由在單個Dirac點上接觸的2個色散帶和1個零能平帶組成的具有對稱性的三能帶結構,這也是Lieb lattice模型最為顯著的特點。對于2D Lieb lattice模型,在沒有自旋軌道耦合作用時,其能譜中的2個色散帶始終有1個接觸點位于零能平帶上,也就是說其能帶間隙始終是閉合狀態。而若想打開其能帶間隙則必須要施加1個非零的自旋軌道耦合作用[13]。這不禁引起了本文思考,這一特性在3D Lieb lattice模型中是否也同樣適用。

本文在2D Lieb lattice模型中施加層間耦合作用,可以得到如圖1(b)所示的立方結構,該立方結構仍然是由A,B,C 3種原子構成,模型的晶格常數為a。

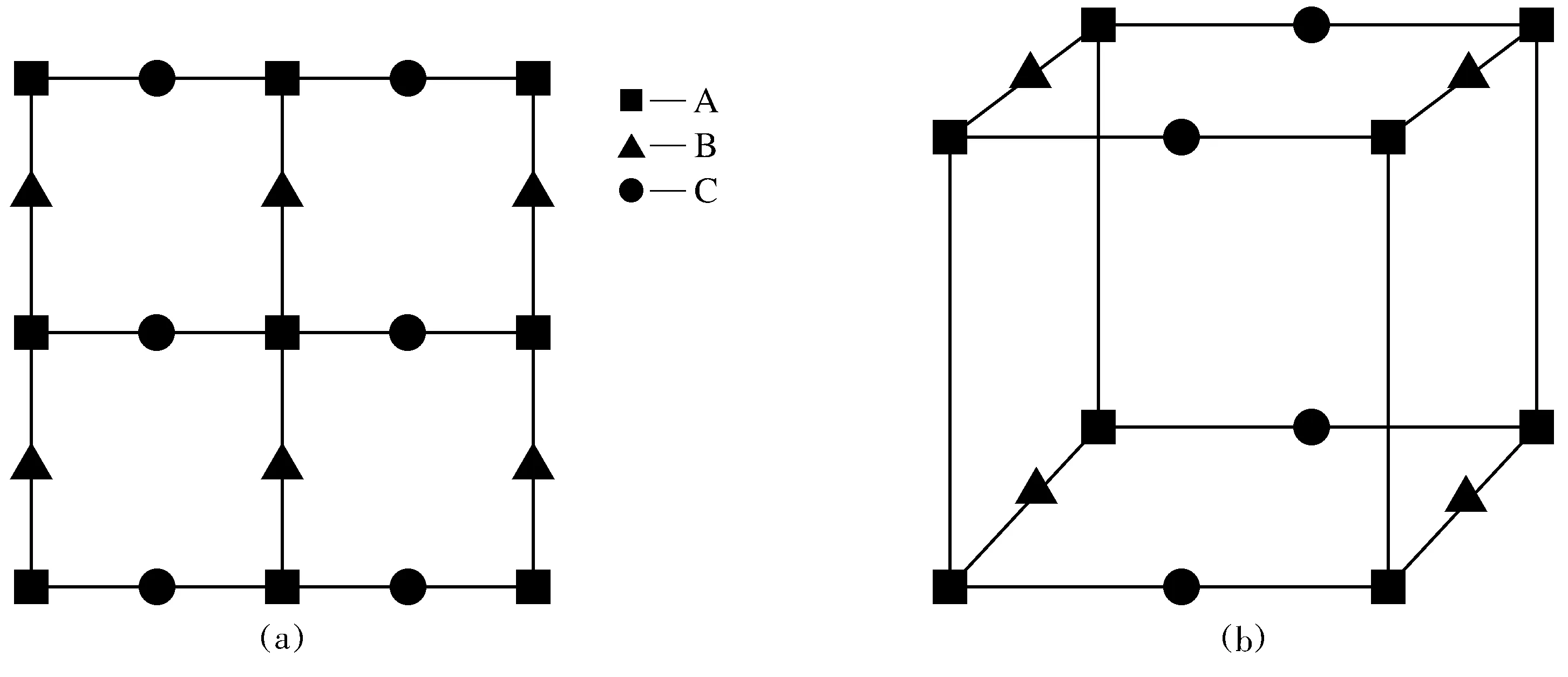
(a)—2D Lieb lattice模型; (b)—3D Lieb lattice模型圖1 Lieb lattice模型Fig.1 Lieb lattice model

在緊束縛近似下,該模型的哈密頓量由以下幾部分組成,可以表示為

H=H0+H1+H2+HI

其中:H0為化學勢項;H1為最近鄰格點之間的躍遷項;H2為次次近鄰格點之間的躍遷項:

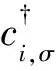
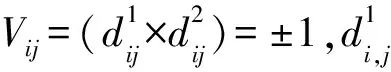
模型的哈密頓量在動量空間可以表示為

基矢為Ψk=(cA,k,↑,cB,k,↑,cC,k,↑,cA,k,↓,cB,k,↓,cC,k,↓)T,在此基礎上,其哈密頓量可以展開成為矩陣的形式:

為方便計算,均取晶格常數a為單位長度1,其中h±(k)可以表示為

其中:Cu=cos(ku);u=x,y,z;Cu/2=cos(ku/2);Su/2=sin(ku/2)。

對此哈密頓矩陣進行對角化,可以得到該立方格子模型的體能帶表達式為

其中Cx±y=cos(kx±ky)。若不考慮次次近鄰躍遷,3D Lieb lattice模型將退化成2D Lieb lattice模型,取λ=0,t′=0,ky=kz=π,取t為單位能量,可以看到圖2(a)所示的處于簡并狀態的能帶圖,由圖像可以觀察到中間的能帶為平帶,上下2條色散帶與該平帶相形成狄拉克錐結構,3條能帶有且僅有1個簡并點在(π,π,π)。

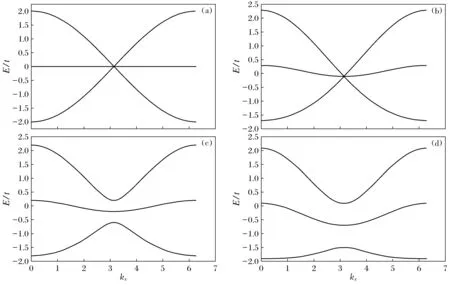
(a)—t=1; μ=0.5;λ=0; t′=0; ky=kz=π; (b)—t=1; μ=0.5; λ=0; t′=0.1; ky=kz=π;(c)—t=1; μ=0.5; λ=0.1; t′=0.1; ky=kz=π; (d)—t=1; μ=0.5; λ=0.2; t′=0.1; ky=kz=π圖2 3D Lieb lattice模型能譜Fig.2 Energy spectrum of 3D Lieb lattice model

若在此基礎上加入層間次次近鄰躍遷的影響,看到如圖2(b)的能帶圖,通過和圖2(a)的對比不難看出其能譜圖像仍為狄拉克錐結構,3條能帶在(π,π,π)點有且僅有一個簡并點。不同的是,加入次次近鄰作用后其中間的能帶在零能附近,為近似平帶。當施加自旋軌道耦合作用在次近鄰躍遷上,即λ≠0時可以得到如圖2(c) 所示的能譜圖像,可以看到當λ≠0時,能帶間打開了一個完整的間隙,并且隨著自旋軌道耦合強度的增加,能隙將越來越大(圖2(d))。

2 3D廣義Lieb lattice模型

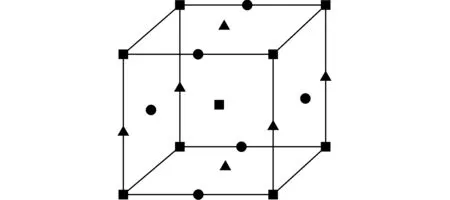
圖3 3D廣義Lieb lattice模型,由A(方形), B(圓形),C(三角形)3個原子組成Fig.3 3D generalized Lieb lattice model, consisting of three atoms: A(square), B(circle) and C(triangle)

上一節本文將2D Lieb lattice模型加入層間耦合從而得到1個新的3D Lieb lattice模型,討論了其能譜隨自旋軌道耦合強度的改變從而發生的變化,得到的結果與2D Lieb lattice模型類似,即要想打開能帶間隙消除簡并點的必要條件是施加非零的自旋軌道耦合作用,那么對于這一結論是否適用于3D廣義Lieb lattice模型呢?3D廣義Lieb lattice模型同樣是由A,B,C 3種原子組成,值得注意的是,3種類型的原子不僅存在于立方體的邊和面心上,在立方體的中心還存在1個A原子(圖3)。

在緊束縛近似下,該模型的哈密頓量可以表示為

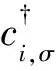
該哈密頓量的基矢為

Ψk=(cA,k,↑,cB,k,↑,cC,k,↑,cA,k,↓,cB,k,↓,cC,k,↓)T,

在此基礎上,哈密頓矩陣可表示為

h±(k)可以表示為

其中:Cu=cos(ku);Cu/2=cos(ku/2),u=x,y,z。

選取參數t1= 1,t2= 0.8,t3= 0.5,t4=0.1,t5= 0.2,ky=kz=π,并對角化該矩陣得到圖4(a),由圖像可知,在未施加自旋軌道耦合作用時,廣義三維Lieb lattice模型的能譜圖像仍是由3條能帶構成且在低能下呈狄拉克錐結構,上下2條色散帶與中間帶有1個簡并點, 中間帶在零帶附近為近似平帶。

若只在該模型其中1個平面(如XY平面)的次近鄰躍遷上施加自旋軌道耦合作用時,

其中:Sx/2=sinx/2;Sy/2=siny/2;λ為自旋軌道耦合強度。

選取參數kz=π,t3=t4=t5時對矩陣進行對角化可以得到三維廣義Lieb lattice模型的能帶表達式為

其中:Cu=cosku,Cx±y=cos(kx±ky)。

取各個躍遷項躍遷強度參數為t1=1,t2=0.8,t3=0.5,t4=0.1,t5=0.2,λ=0.2,且kz=ky=π時,可以得到圖4(b)所示的能譜圖。

(a)—無自旋軌道耦合作用; (b)—在XY平面施加自旋軌道耦合作用圖4 3D廣義Lieb lattice模型能譜圖Fig.4 Energy spectrum of 3D generalized Lieb lattice model

在XZ與YZ平面的次近鄰躍遷上施加自旋軌道耦合作用得到的帶隙結構與在XY平面施加自旋軌道耦合作用相似。因此,若要在能帶中間打開1個完整的帶隙,可以通過在模型空間中的任意1個平面施加自旋軌道耦合作用來實現。

3 結 論

本文在自旋軌道耦合作用存在的情況下研究和討論了2種3D Lieb lattice模型的能譜結構。研究結果表明,在3D Lieb lattice模型中,加入次次近鄰躍遷會影響其能譜圖像中的零帶,使其產生帶寬成為近似零平帶。若在模型中加入自旋軌道耦合作用,當自旋軌道耦合強度為零時,其能譜由3條能帶組成,且3條能帶有且僅有1個簡并點,只有在自旋軌道耦合強度不為零時,才能打開其能帶間隙,并隨著自旋軌道耦合強度的增加,能帶間隙會逐漸變大。

Lieb lattice模型為研究拓撲物質的特性和拓撲量子相變提供了可能,在該模型上施加自旋軌道耦合作用時其能帶間隙被打開,這一研究有助于實現物質由其拓撲半金屬性到拓撲絕緣體性的轉變。