多元研讀促設計 深入理解創靈動

高暉

研讀教材一直是教師工作的重要內容，它關系到教師的課堂設計、課堂組織與實施，更關系到教學目標的實現、教育目標的達成。教材也是學生從事數學學習的基本素材，它為學生的數學學習活動提供了基本線索、基本內容和主要的數學活動機會。

本文以人教版數學六年級上冊“數學廣角——數與形”為例，通過發現、質疑、創造式的多元化研讀方式和對教材縱橫向對比聯系，將教學設計做了大刀闊斧的“改革”。

一、內容背景的發現與滲透

人教版數學六年級上冊“數學廣角——數與形”例1的教學內容是：

基于小學生的年齡特征和認知特點，教材編排時通常只呈現相應知識點以及相關數學思想方法的滲透，而知識點背后一些深層次的原理或相關背景等教材在編排時進行了取舍。研讀教材時如果能挖掘發現這些背后隱藏的部分，從而可以讓教師立足于“高觀點”理解教材。

例1是讓學生運用數形結合探究“正方形數”的規律。“正方形數”“三角形數”等統稱為“形數”。古希臘畢氏學派對“形數”就已經有著深入的研究。基于此背景，設計時我在開篇加入了畢氏學派“萬物皆數”思想和“形數”的介紹，讓學習建立在數學史的基礎上了解知識的產生和發展的過程，激發學習數學的興趣。

二、內容編排的對比與聯系

“數與形”的內容是2013年人教版義務教科書修訂版新增的內容，而在北師大版數學五年級上冊“數學好玩”的板塊中編排了“點陣中的規律”。（如下圖）

兩個版本的編排設計有著異曲同工之妙，人教版“以形助數”，北師大版“以數解形”。通過對比和聯系兩個版本教材的編排，我將北師大版點陣中的規律和“形數”相結合，形成教學設計。

片段一：

（課件出示：9）

師：同學們還記得剛才老師介紹時9所代表的含義嗎？

生：理性。

師：在研究9的時候，學者撿了9顆石子并擺成了一個我們很熟悉的圖形，猜猜是什么圖形？

生：三角形，正方形……

師：用你們手中的圍棋子試著擺一擺。

生：正方形。

師：觀察這個圖形，你能從中發現與9相關的一些算式嗎？

生：3×3=9，1+3+5=9，1+2+3+2+1=9…

師：從這些算式中，你發現什么特點？

生：3×3就是3的平方，1+3+5是連續的奇數相加，1+2+3+2+1是連續自然數再倒回去相加……

師：當時學者們也發現了這樣的特點，1+3+5=3×3=32=9。

師：你們還能找到和9有著相同特點的數字嗎？

生：1=1×1=12=1，1+2=2×2=22=4，1+3+5=3×3=32=9…

師：觀察這些算式，你能發現什么規律嗎？

生： 從1開始的連續奇數的和等于奇數個數的平方。

師：1、4、9、16…這些數字學者們還給它們起了個名字——“正方形數”。

數形結合思想的運用可以說一直貫穿于小學數學的學習中，在學生已經擁有了很多數與形結合的經驗后，通過觀察和計算1、1+3、1+3+5、1+3+5+7…既能發現加數的規律（從1開始的連續奇數相加），又能發現和的規律（都是連續的正方形數），在發現規律的基礎上，通過推理，再引導學生把規律應用于一般的情形，解決問題。

三、內容資源的選擇與整合

創造性地使用教材，做到尊重教材和靈活處理教材，充分發揮教材資源作用，有機結合教材的例題資源和練習資源等可以讓教學設計更加靈動。設計中，我將例1和教材第109頁練習二十二的第2小題結合，進一步對“形數”進行探究，深化數形結合思想。

片段二：

課件出示：10

師：它代表什么含義？

生：完美。

師：你能用剛才的方法發現10的特點嗎？

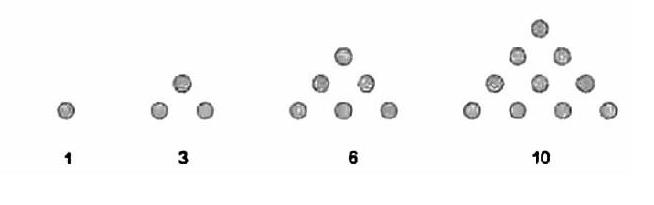
生：我們把10顆棋子擺成了一個三角形，從而得到10=1+2+3+4，是連續自然數的和。

師：還有和10有著一樣特點的數嗎？

生：還有1、3、6、15…都可以寫成連續自然數的和。

師：你們能給這些數也起一個名字嗎？

生：三角形數。

師：觀察兩個相鄰的“三角形數”的和是？

生：是“正方形數”！把一個數補到另一個數空缺的地方就形成了一個正方形。

師：我們已經認識了“三角形數”“正方形數”，那么還有像它們一樣有特點的數嗎？

生：五邊形數、六邊形數……

師：對，這樣的數我們都稱之為“形數”，這些“形數”的特點等著大家下來去探究、去發現。

通過例1“正方形數”的探究學習，學生自主探究練習二十二第2小題“三角形數”的規律，并建立兩種數的聯系發現“相鄰兩個三角形數之和等于一個正方形數”的規律。探索過程中學生充分經歷了數形結合思想的運用，感受到數與形的緊密聯系，同時埋下了繼續探究的種子。

教材作為教師進行教學活動的主要依據，也是學生進行學習活動的主要基礎，故對教材多元化研讀、深入理解教材內容不僅是教師駕馭教材、駕馭課堂，促進完善教學設計的有力保證，也是創設靈動智慧的數學課堂的前提基礎。