基于FPGA的柔性機械臂多路無刷直流電機控制系統設計*
吳鵬飛,祖鳳丹,陳景元,李昃雯,宛俊偉
(上海航天控制技術研究所·上海·201109)
0 引 言
無刷直流電機(Brushless DC Motor,BLDCM)具有結構簡單、長壽命、效率高、低噪聲的優勢[1],廣泛應用于機械臂的關節驅動,工業中的剛性機械臂通常擁有3~6個自由度,驅動電機通常設置于關節處,這導致剛性機械臂比較笨重,自由度較少和靈活性差。
柔性機械臂憑借其特殊的柔性結構和超冗余自由度的特點,使得它在狹小的作業空間中游刃有余,本文研究的鋼絲繩索驅動的柔性機械臂各關節共由16個無刷直流電機驅動,具備狹小空間靈巧運動的功能,可應用于航空航天、國防安全、搶險救援等狹小領域作業[2]。16個無刷直流電機設置于柔性機械臂的底部驅動箱中,從而減小了各個關節的質量。傳統的電機控制通常采用數字信號處理(Digital Signal Processing,DSP)芯片,文獻[3]中提出采用DSP作為無刷直流電機控制器,雖然DSP能快速運行較為復雜的電機控制算法,但DSP外圍電路較為復雜,并且用戶接口數量少,單個DSP芯片無法保證16個無刷直流電機高精度、協調運動。文獻[4-5]提出采用多個DSP芯片進行協同控制電機運動,這種方法雖然可以彌補DSP用戶接口數量不足的缺陷,但是多個DSP勢必導致外圍電路更加復雜,并且不同的DSP控制柔性機械臂不同關節的電機,各個電機的同步精度較低,設計程序時還要兼顧其它DSP的控制,增加了軟件設計的難度。可編程邏輯門陣列(Field Programmable Gate Array,FPGA)具有現場可編程、并行處理的優勢,并且具有幾百個I/O引腳可供用戶分配,一片FPGA芯片可以同時控制多路電機,提高了繩驅柔性機械臂各路電機的同步性。采用傳統的PID算法控制精度低、抗柔性負載擾動能力差,導致各路電機的位置跟蹤精度下降,文獻[6]提出了改進差分進化算法優化的PI控制器用于無刷電機的控制,這種算法是一種自適應全局優化算法,改進的PI控制器具有收斂速度快、魯棒性更好的優點,這種改進算法也存在一定的缺陷,隨著進化代數的增加,會使得種群的多樣性變小,從而過早收斂到局部極小點。文獻[7-15]提出了許多其它改進PID控制器的辦法,比如自適應PID控制、滑模控制、神經元PID控制,這些控制方式確實能提高PID控制器的參數自適應能力和抗擾動能力,在衛星飛輪、壓電驅動平臺、機器人控制器中得到了驗證。文獻[12]中采用神經元PID控制器用于解決PID參數調節困難的問題,取得了較好的仿真效果。神經元PID控制算法具有結構簡單、抗非線性負載擾動能力強的特點,非常適合在并行處理速度極快的FPGA芯片中運行,因此本文采用一片FPGA芯片作為16路無刷直流電機的主控芯片,使用改進后的有監督Hebb學習算法設計單神經元自適應PID控制器,在線調節PID參數,并且完成了位置插補算法、16路電流信號采集處理、16路旋變位置信號采集處理等功能,程序設計采用自頂向下的設計方法,各個功能進行模塊化設計,便于程序的修改。
1 系統工作原理
本文的柔性機械臂多路無刷直流電機控制系統框圖如圖1所示。
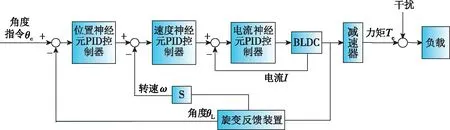
圖1 無刷直流電機控制系統框圖
整個控制系統采用FPGA芯片、電機驅動芯片MSK4300、AD芯片、旋變解碼芯片AD2S80、16個無刷直流電機組成,如圖1所示,位置環、速度環和電流環控制器均在FPGA中實現,其中,三環控制器采用改進型神經元自適應PID控制器。
位置環作為三環控制的最外環,控制周期為5 ms,速度環控制周期為1 ms,電流環追求響應速度,同時要兼顧電流采集芯片AD574的采集速度,電流環控制周期最短,為500 μs。數字PID控制器的功能就是根據電機控制模塊中的控制參數和給定值與反饋值的偏差完成閉環計算的過程,并將計算結果給到速度閉環控制模塊。使用旋變獲取電機的位置,運動過程中不會丟步,保證了位置控制精度。速度環和電流環的設計與位置環的設計方法一致。
傳統的PID算法存在積分飽和現象,即系統存在一個方向的偏差,積分不斷累加增大到很大的值,一旦出現反向偏差,積分很難在短時間內消除,從而產生超調現象[3]。為了解決此問題,本文對位置環、速度環和電流環均進行了限幅,具體實現方法是對積分項進行限幅,當積分項超過一定值時,積分項便不再累加,從而解決了傳統PID超調大的問題。同時本文中沒有使用乘法器,而是靠移位實現乘法運算,這很大地節省了FPGA的資源,提高了運算速度。
電機驅動控制器FPGA功能框圖與對外接口如圖2所示。
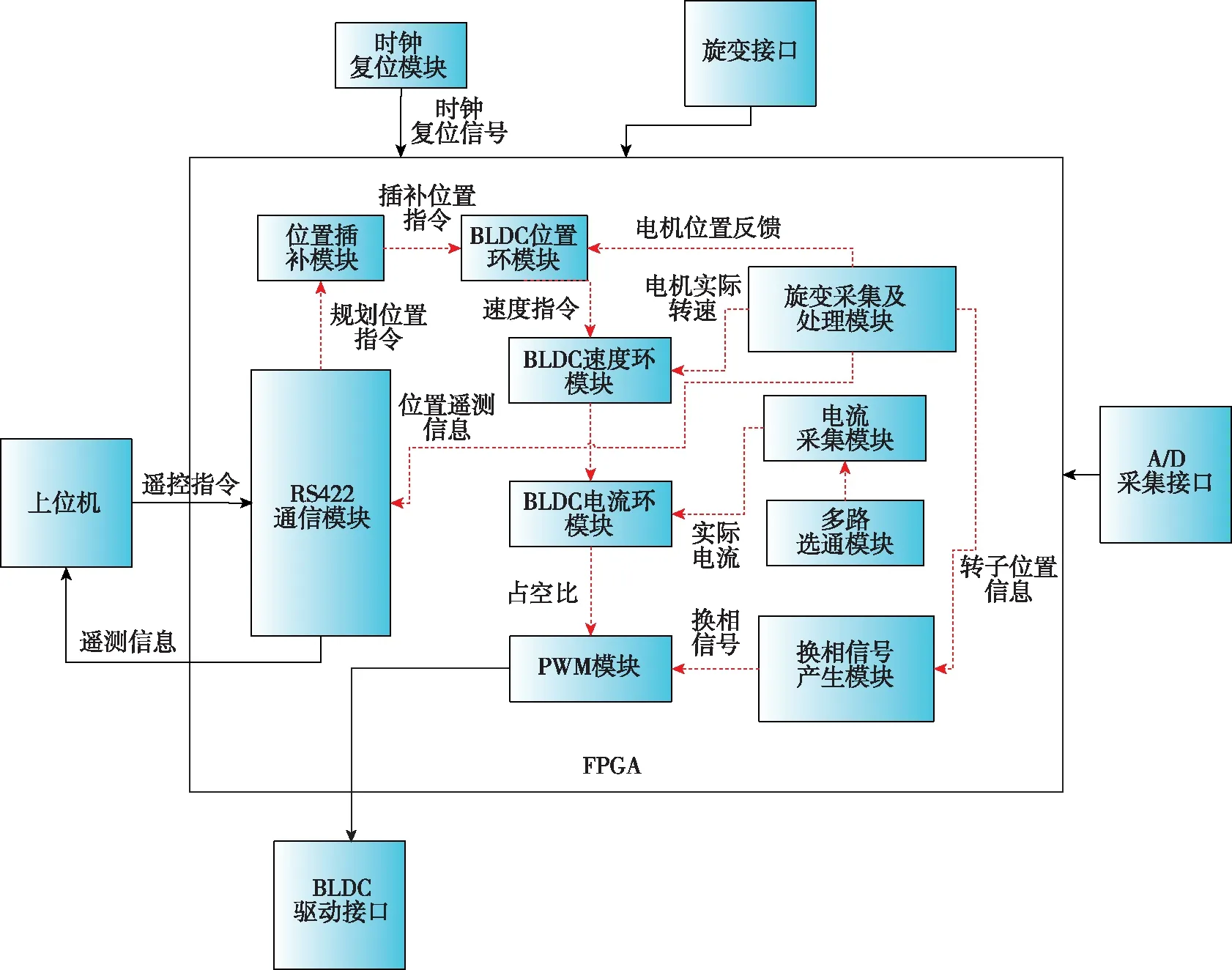
圖2 FPGA功能框圖與對外接口
2 系統方案及控制器設計
2.1 神經元自適應PID控制器設計
為了克服PID算法的抗柔性負載擾動能力差、位置跟蹤精度差的缺陷,運用有監督的Hebb學習算法設計出單神經元自適應PID控制器。
單神經元PID調節器的結構比較簡單,由于PID算法的位置式公式為
(1)
將式(1)中的u(k)減去u(k-1)可以得出PID的增量式算法:
Δu(k)=Kp[e(k)-e(k-1)]+Kie(k)+
Kd[e(k)-2e(k-1)+e(k-2)]
(2)
考慮到有監督的Hebb學習規則更有利于學習結果不停地逼近期望結果,容易實時控制,因此采用有監督的Hebb學習規則更新權值。根據式(2)的形式,單神經元控制器中,輸入層可以設為5個輸入,分別是e(k)、e(k-1)、e(k-2)、u(k-1)、u(k),其中,e(k)為給定和反饋的誤差值;輸出層為u(k);權值為w1(k)、w2(k)、w3(k)。控制器的輸出為
(3)
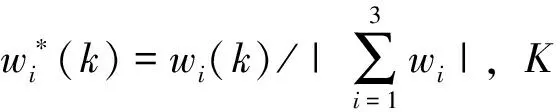
x1(k)=e(k)
(4)
x2(k)=e(k)-e(k-1)
(5)
x3(k)=e(k)-2e(k-1)+e(k-2)
(6)
對式(3)進行改進,在傳統的有監督的Hebb學習規則中引入實際經驗,即將xi(k)=e(k)改為xi(k)=e(k)+Δe(k),其中Δe(k)=e(k)-e(k-1)。
在設計單神經元自適應PID控制器時,需要注意學習規則的選取、神經元比例系數的選取、學習率的選取等。
2.2 電流采集方案
整個電流采集設計流程為:收到采樣起始信號后打開計數器使能,并設置模擬多路選通使得每個模擬多路選通開關都選擇1通道。計時40 μs至模擬多路選擇完成,啟動AD574模塊進行采樣,進入內層狀態機讀取4個AD芯片的電流數據。采樣完一輪(4個)電機電流后,多路開關切換到第2通道,繼續等待40 μs至多路開關穩定,再進行第二輪電機電流的采集,總共進行4輪電機電流的采集,從而完成16路電機電流的采集,FPGA程序設計流程如圖3所示。
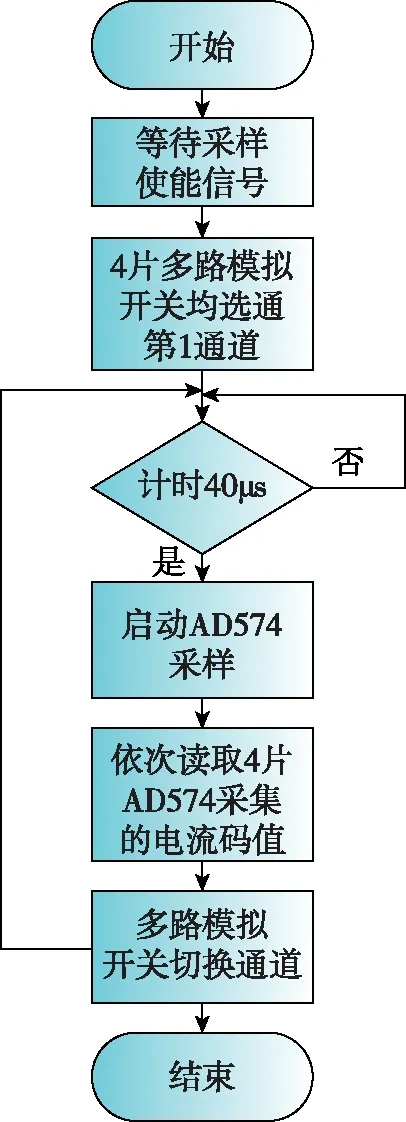
圖3 16路無刷直流電機電流采集流程圖
2.3 旋變位置信號采集方案
旋變位置信號由AD2S80解碼芯片解碼得到,16路無刷直流電機的位置數據可以采用輪詢的方式讀取到FPGA中,因為位置環周期是5 ms,16路旋變輪詢一次的周期是9.6 μs,足以滿足位置環的計算。這種方案可以有效減少總線隔離芯片的使用,并且16路旋變解碼芯片可以復用相同的數據引腳,從而極大地減少FPGA的I/O引腳使用。
旋變角度采集模塊主要用于16路無刷直流電機位置角度的采集和處理,用于16路無刷直流電機的換向控制和電機位置和速度閉環控制,根據AD2S80的采樣時序,設計FPGA程序。
旋變采集模塊軟件設計流程圖如圖4所示。
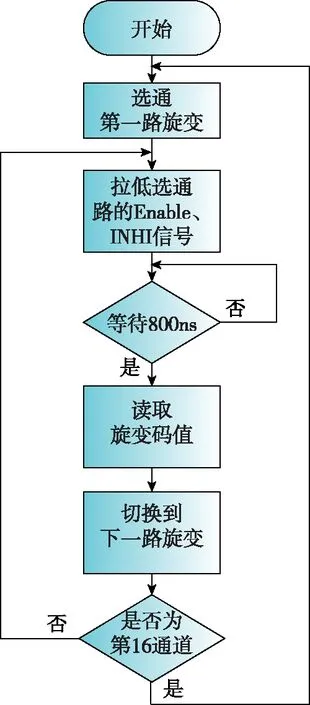
圖4 旋變采集流程圖
2.4 運動插補方案
運動插補主要應用于數控機床和機器人運動控制中,插補方式有直線插補、圓弧插補、樣條線插補等,在本文中,考慮到FPGA的邏輯資源有限,選擇使用較為簡單的直線插補算法。
運動插補模塊主要目的是為了讓電機運動更加柔順,在柔性機械臂運動控制中,CPU負責運動規劃算法,每100 ms給電機控制FPGA發送一個位置規劃指令,FPGA負責各個關節無刷直流電機的三環(位置環、速度環和電流環)控制,假設沒有使用運動插補模塊,由于位置環的控制周期為5 ms,因此每次CPU發送一個位置規劃指令,位置環接收到后,由于該位置規劃值較大,因此電機達到速度限幅值以最大速度運轉,電機以最大速度運行一定的時間后到達期望位置(規劃位置),此時電機會停下來,電機實際運行的時間可能只用了幾十毫秒(假設30 ms)就運行到了期望位置處,那么剩下的時間里(70 ms),電機是處于不運動的狀態。
如果使用運動插補模塊,將100 ms時發送的位置分成20個位置點,FPGA每間隔5 ms發送一個位置點給位置環,這樣一來,就可以有效避免電機提前運動到CPU發送的期望位置處。FPGA進行運動插補時,CPU控制周期為100 ms,位置環計算周期為5 ms,因此,首先需要設計一個5 ms計數器子模塊,FPGA每次接收CPU發送的位置規劃指令后產生一個觸發信號,觸發5 ms計數器進行計數。為了進行位置細分,需要設計一個除法器子模塊,為了節省FPGA邏輯資源,采用移位減法的方式進行除法器設計,被除數為位置細分模塊產生的位置增量,除數為細分數20,計算得到商和余數,輸出給位置細分模塊。設計一個位置細分子模塊,當接收到新的位置指令后,將新位置減去上一個控制周期接收到的位置,即計算出100 ms的位置增量,該位置增量作為輸出量給到除法器模塊,細分時,如果除法器模塊存在除不盡的情況,那么該位置細分子模塊需要將余數均分到細分后的位置。
舉例說明,如果第100 ms時,CPU發來一個規劃位置指令為100,第200 ms時,發送第二個規劃位置指令為203,位置細分接收到該指令后,將這兩個位置進行作差得到103,作為被除數傳給除法器模塊,除以20后得到的商為5,余數為3,該計算結果傳給位置細分模塊,每間隔5 ms產生一個細分后的位置指令給位置環模塊,即:5,5,5,5,5,5,5,5,5,6,6,6,5,5,5,5,5,5,5,5。
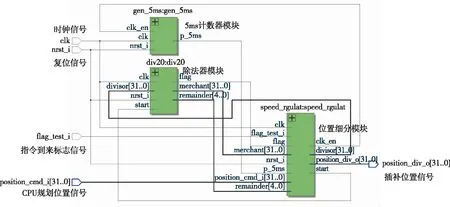
圖5 插補模塊RTL原理圖
3 仿真驗證
搭建改進型Hebb神經元自適應PID控制器Simulink仿真模型,該控制器采用S函數的形式完成。
仿真條件參數設置如下:所選BLDC電機極對數pn=4,定子電感Ld=Lq=30mH,定子電阻r=7 Ω,電機轉矩常數fm=0.12256(Nm/A),轉動慣量1.39×10-6(kg·m2)。
輸入正弦信號y=5.41sin(2πt/250),運動期間引入外部干擾,對比經典PID控制和改進型Hebb神經元自適應PID控制器的控制效果,仿真結果如下:
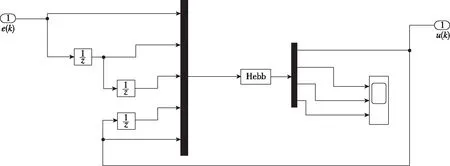
圖6 神經元PID控制器
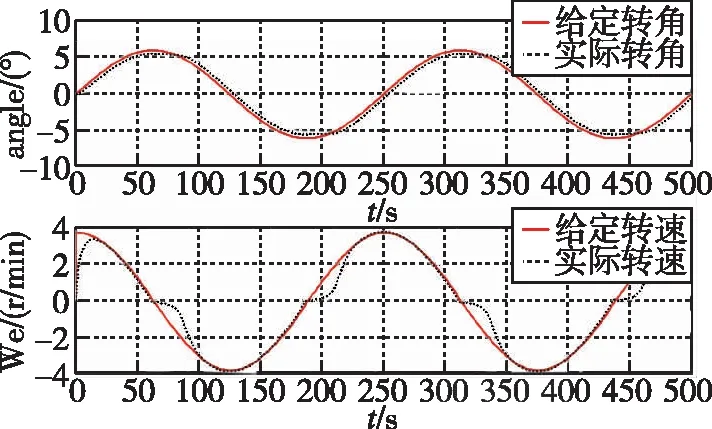
圖7 經典PID控制的位置追蹤和速度追蹤情況
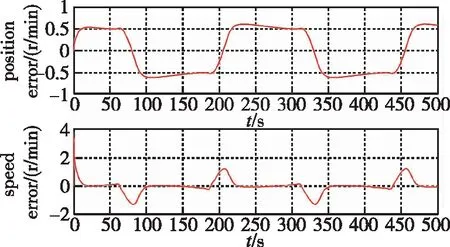
圖8 經典PID控制的位置與速度跟蹤誤差情況
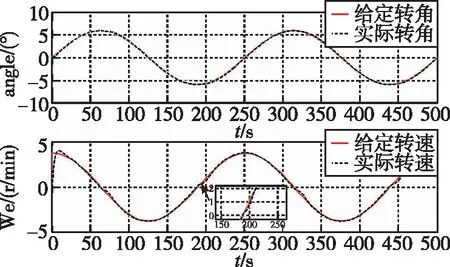
圖9 改進型Hebb神經元自適應PID控制器的位置追蹤和轉速追蹤情況
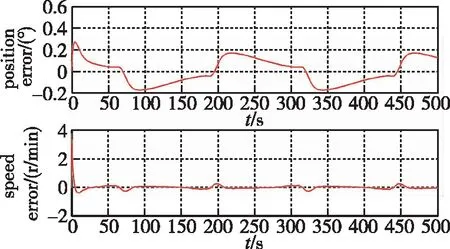
圖10 改進型Hebb神經元自適應PID控制器的跟蹤誤差情況
從圖7~圖10看出,采用神經元自適應PID控制器的跟蹤精度更高,相比于傳統的PID控制,位置誤差縮小了50%,引入擾動時,轉速波動大幅降低,抗擾動能力明顯提升。
4 實驗驗證
為了驗證控制方案的正確性和系統的性能,搭建柔性機械臂實驗平臺,整個柔性機械臂分為驅動箱和臂兩大部分,臂由關節、臂桿、鋼絲繩索組成,驅動箱包含了16個無刷直流電機和驅動控制器,主控芯片采用一片ALCTEL的FPGA。實驗中選用的無刷直流電機額定電壓為31 V,其它參數選取和上一節仿真時設置的一致。
測試各路電機運行效果,通過CPU發送階躍位置規劃指令給電機控制FPGA,上位機實時繪制各路電機位置、誤差、電流、轉速曲線。
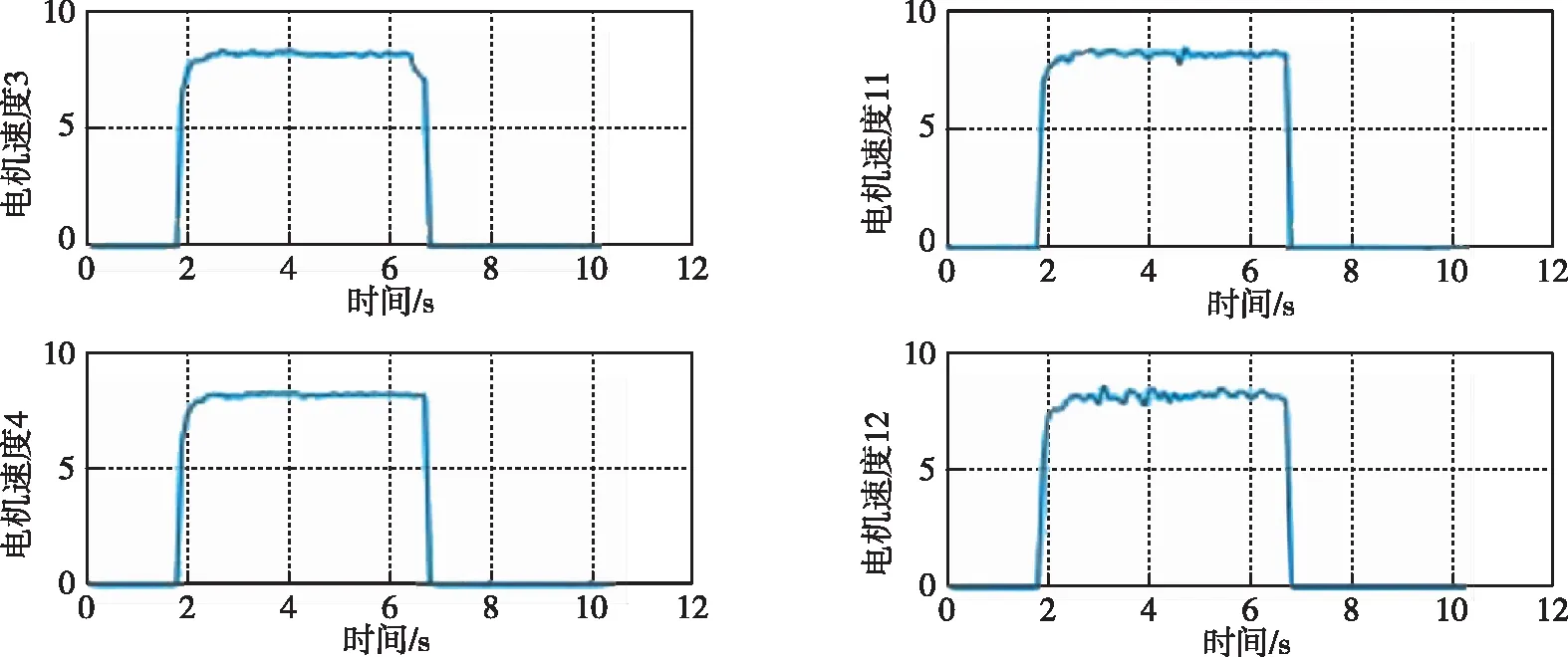
圖11.部分電機速度曲線
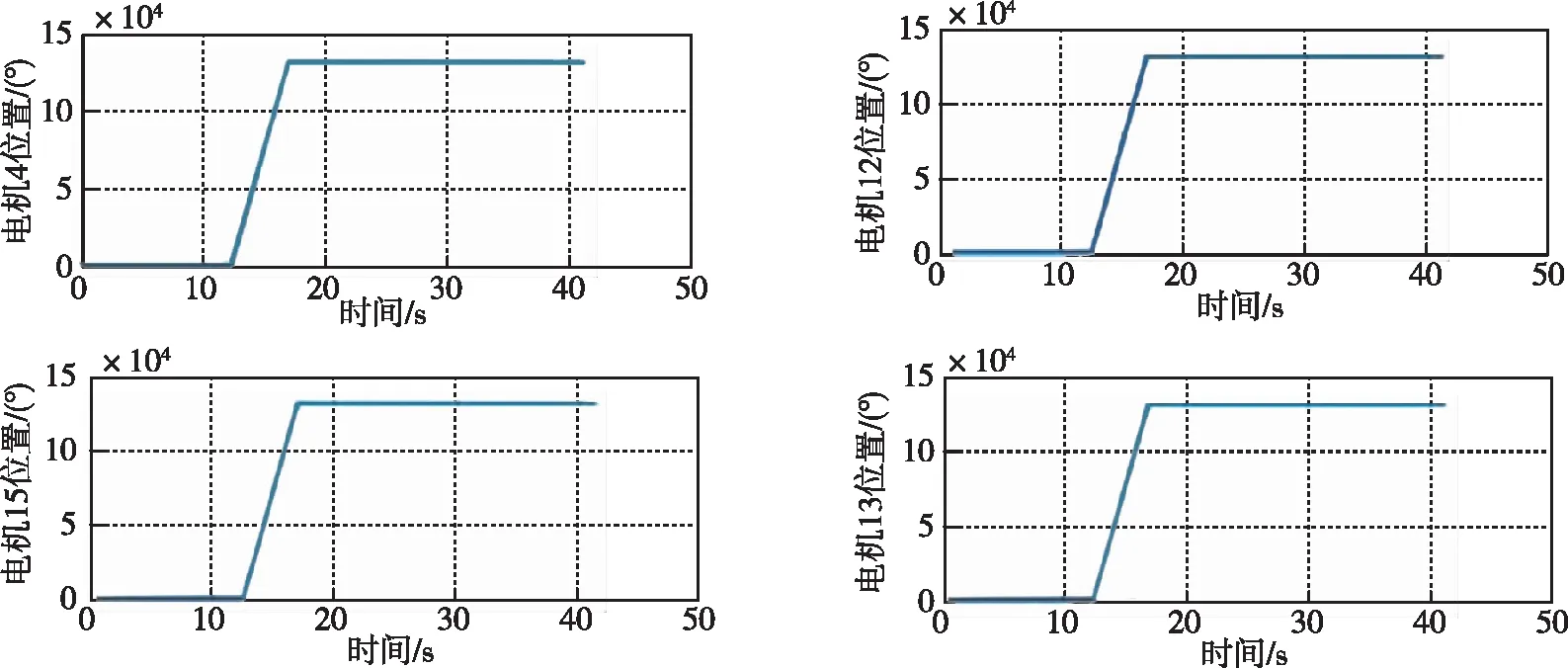
圖12 部分電機位置曲線
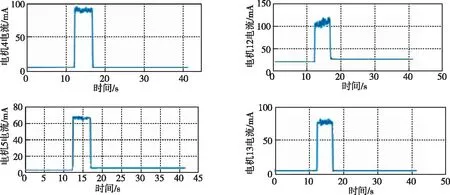
圖13 部分電機電流曲線
從圖11~圖13的實測結果可以看出,速度波動較小,電機運行平穩,各路電機同步性較好,穩態位置誤差為25碼值,轉換為角度誤差為0.137°。
5 結 論
本文提出的基于FPGA實現的多路無刷直流電機控制方案可以適應柔性機械臂的驅動,每個關節的無刷直流電機運動同步性、協調性良好,力矩輸出平滑,可以確保柔性機械臂運動過程的柔順性,實驗驗證了本文設計的驅動控制器能確保在0~0.35(Nm)不同負載下,各個關節的電機定位精度優于0.2°。

