含砂天然氣節流閥沖蝕仿真模擬及結構改進

錢東良, 田輝芳

(山西省燃氣規劃設計研究院有限責任公司，山西太原030024)

1 概述

由于天然氣中含有泥砂，管道輸送介質為氣-固兩相流，在運行過程中，節流閥內部長時間受到氣-固兩相流(特別是其中的砂粒)的沖擊，易發生沖蝕和刺漏等現象，嚴重影響生產安全。在節流孔處，由于流通面積減小，其壓力、速度以及粒子的流動軌跡都發生改變，故此處常常是發生沖蝕較嚴重的部位[1]。以楔形節流閥閥芯為例，楔形節流閥閥芯失效現場實物見圖1[2]，閥芯迎流面受到的沖蝕破壞較為嚴重，直接導致其節流功能失效。

圖1 楔形節流閥閥芯失效現場實物

目前，關于節流閥的研究已取得一定的進展，文獻[2-4]中對節流閥進行了流場分析，得出其內部流場的分布規律，但是，針對不同類型的節流閥內部易產生沖蝕的具體位置及防護措施并未全部給出。因此，有必要在已有研究的基礎上做更進一步的仿真模擬。

本文采用Pro/E 5.0軟件建立錐形節流閥和楔形節流閥的幾何模型，利用ANSYS Fluent 14.5軟件建立仿真模型，模擬得到節流閥內產生沖蝕的具體位置，并在此基礎上，針對閥芯進行一定程度的結構優化，通過仿真模擬驗證其有效性，從而實現減緩沖蝕的目的。

2 幾何模型的描述

節流閥主要由閥體、閥芯、彈簧和調節手輪等部件組成，通常情況下豎直安裝，通過閥芯的豎直移動來改變節流孔的流通面積，從而達到節流效果。以規格為DN 50 mm錐形節流閥為例，其簡化三維模型見圖2，結構尺寸見圖3，圖3中標注的尺寸均為內壁尺寸，相應的單位為mm，圖3中設定的開度是某一工況下的開度，本文以此開度為例進行模擬。

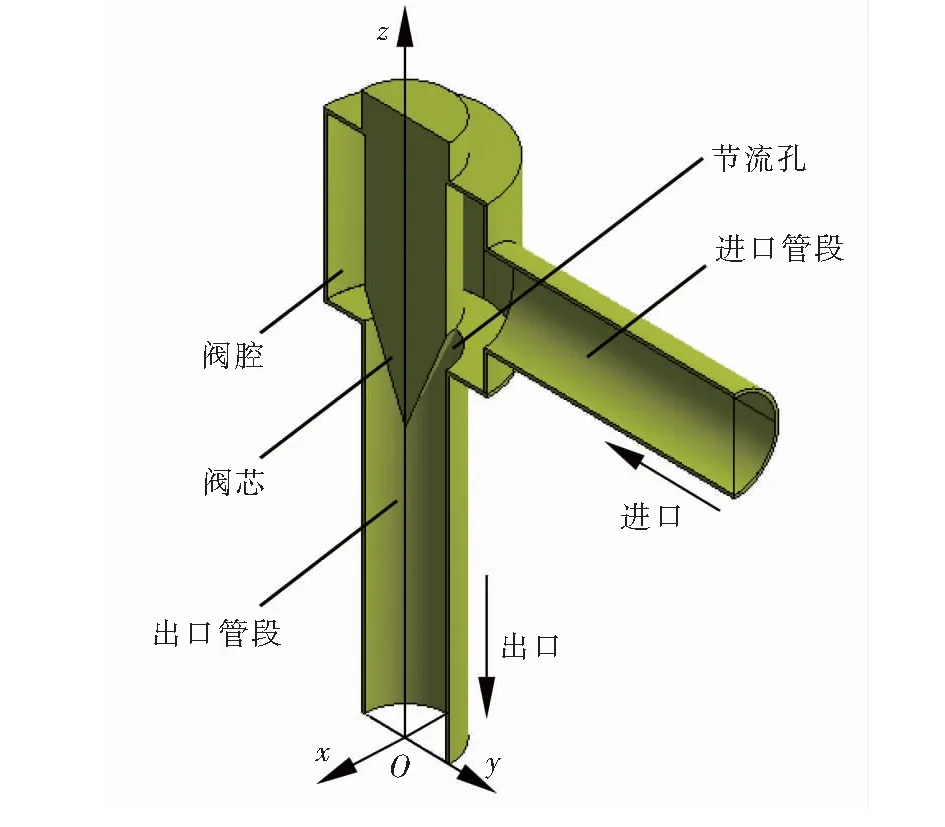
圖2 DN 50 mm錐形節流閥的簡化三維模型

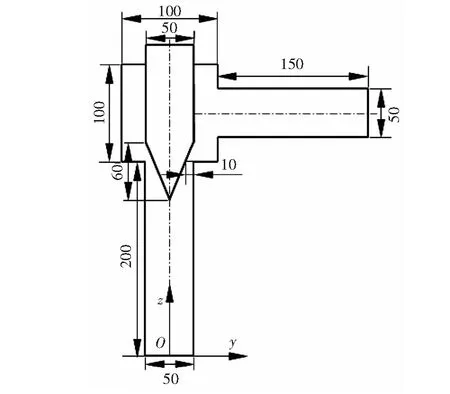
圖3 DN 50 mm錐形節流閥的結構尺寸

圖2中,三維坐標系的建立以出口端面的圓心為原點O，x軸和y軸均在出口端面所在的水平面上，與進口管段中軸線相垂直的是x軸，與進口管段中軸線相平行的是y軸，閥芯中軸線為z軸。為了方便了解簡化模型的內部結構以及節省模擬計算的時間，以yOz平面為中心面進行對稱剖分，取其一半進行分析。在三維模型中，彈簧和調節手輪等部件簡化為圖2中與閥芯相連且凸出閥腔的圓柱部分。節流閥垂直安裝，即重力加速度g的方向為-z方向，流體流入方向為-y方向，流體流出方向為-z方向。進口端面、進口管段內壁、閥腔內壁、閥芯外壁、出口管段內壁、出口端面及yOz平面共同組成的空間區域即為計算域，利用ANSYS Fluent 14.5進行建模分析時，只需研究該計算域即可。

本文以應用比較廣泛的錐形節流閥和楔形節流閥為基礎研究對象，并在其現有結構的基礎上，針對閥芯進行一定的結構改進，其中，將錐形節流閥閥芯的頂端(尖端)改為圓臺狀，將楔形節流閥閥芯改為圓臺狀閥芯或三段式閥芯，得到3種優化的結構形式，分別為圓臺狀閥芯錐形節流閥、圓臺狀閥芯楔形節流閥和三段式閥芯楔形節流閥。利用Pro/E 5.0建立不同類型節流閥的三維幾何模型，錐形節流閥和圓臺狀閥芯錐形節流閥的幾何模型見圖4，楔形節流閥、圓臺狀閥芯楔形節流閥、三段式閥芯楔形節流閥的幾何模型見圖5。

圖4 錐形節流閥和圓臺狀閥芯錐形節流閥的幾何模型

圖5 楔形節流閥、圓臺狀閥芯楔形節流閥、三段式閥芯楔形節流閥的幾何模型

3 網格劃分

將建立的幾何模型導入ANSYS Workbench中的Geometry里，應用Fill功能填充計算域，完成后將其導入Mesh中劃分網格。以進口處的網格劃分為例，進口處網格劃分見圖6。

整個模擬區域可分為湍流核心區和邊界層區。在網格劃分的過程中，湍流核心區采用自動劃分網格，以四面體網格為主。邊界層區添加邊界層網格，對近壁面處的網格進行局部加密，在計算過程中，使用壁面函數法來處理該區域，壁面函數法的具體分析詳見4.5.1條，其目的在于將壁面上的物理量和湍流核心區相應的物理量聯系起來。邊界層網格的劃分方式采用First Layer Thickness，邊界層網格劃分需要設置的參數為：第1層網格高度(First Layer Height)為1.0 mm，邊界層數(Maximum Layers)為5層，網格漸變率(Growth Rate)為1.05，這樣能夠保證無量綱距離y+處于(30，60)范圍。

4 數學模型

4.1 數學模型概述

本文研究的對象是氣-固兩相流，其中，天然氣作為連續相，砂粒作為離散相。為了簡化模擬計算，本文假定天然氣介質為不可壓縮流體且流動是穩態的，天然氣的密度不隨空間位置和時間變化，流場處于完全發展的湍流狀態，忽略流體分子之間黏性的影響，在該假定情況下能夠滿足工程仿真模擬精度的要求。

采用ANSYS Fluent 14.5軟件進行沖蝕仿真模擬需要建立合適的數學模型，它主要包括：內部流場計算、顆粒軌跡計算和沖蝕速率計算。連續相采用RNGk-ε湍流模型，離散相采用離散相模型，通過交替求解連續相控制方程和離散相運動方程來實現連續相與離散相的雙向耦合；沖蝕速率模型采用ANSYS Fluent 14.5中定義的沖蝕速率公式；近壁面區域采用標準的壁面函數法進行處理；采用有限體積法對控制方程進行離散化處理；采用SIMPLE算法求解速度場與壓力場的耦合。

4.2 湍流模型

節流閥連續相計算必須選用合理的湍流控制方程。根據流體動力學理論，RNGk-ε湍流模型對具有分離和二次流的湍流流動具有較好的模擬性[5]，既適應于高雷諾數的湍流流動，也適應于低雷諾數的湍流流動，其模型常數是利用重整化群(RNG)方法精確推導出來的[6]。RNGk-ε湍流模型是半經驗公式。

k方程見式(1)[5]：

Eg+Eb-ρε-EM+Sk

(1)

式中ρ——天然氣(不含砂粒)密度，kg/m3

k——湍流動能，J

t——時間，s

i——取值為1、2、3，分別對應x軸、y軸、z軸

ui——速度分量，分別對應x軸、y軸、z軸上的速度分量ux、uy、uz，m/s

xi——對ui求偏導時對應的x軸、y軸、z軸的坐標，m

Prk——k方程的湍流普朗特數

μeff——有效動力黏度，Pa·s

j——取值為1、2、3，分別對應x軸、y軸、z軸

xj——對k求偏導時對應的x軸、y軸、z軸的坐標，m

Eg——層流速度梯度產生的湍流動能，J

Eb——浮力產生的湍流動能，J

ε——湍流耗散率，J/s

EM——湍流流動中波動對整個能量耗散的貢獻，J

Sk——k方程中與實際問題有關的修正項，由用戶自定義，無因次

需要注意的是：ui、xi、xj均為笛卡爾張量記法，均表示1組分量，1個含有3個與坐標相關的獨立變量集合用1個下標表示，例如，對于坐標x、y、z可表示為xi(i=1，2，3)，即x1表示x軸坐標，x2表示y軸坐標，x3表示z軸坐標；對于x軸、y軸、z軸上的速度分量ux、uy、uz可表示為ui(i=1，2，3)，即u1表示ux，u2表示uy，u3表示uz。以上表示方法為流動方程表達式中慣用的張量記法。在式(1)中關于xi、xj的偏導數表示下標i和j分別為1、2、3時的各項之和，即式(2)和式(3)。

(2)

(3)

ε方程見式(4)[5]：

(4)

式中Prε——ε方程的湍流普朗特數

C1ε、C2ε、C3ε——經驗常數，無因次

Rε——ε的函數

Sε——ε方程中與實際問題有關的修正項，由用戶自定義，無因次

4.3 離散相模型

離散相模型將天然氣作為連續相、砂粒作為離散相進行處理，離散相與連續相間通過實時進行質量、動量和能量交換實現雙向耦合求解。離散相模型在應用中忽略砂粒之間的相互作用以及砂粒的體積對連續相的影響，應用離散相模型的前提是離散相的體積分數應小于10%。文獻[7]針對砂粒運動方程、砂粒受力分析、離散相邊界條件的設置以及離散相與連續相的耦合等方面進行了詳盡的分析。

4.4 沖蝕速率模型

節流閥內壁面的沖蝕失效程度可以通過計算全部砂粒在天然氣攜帶下沖擊節流閥內壁而產生的沖蝕速率來表示，沖蝕速率模型采用ANSYS Fluent 14.5中定義的沖蝕速率公式，該沖蝕速率模型在文獻[5]中已經做了詳盡的分析。

4.5 其他相關數值計算方法

4.5.1 壁面函數法

針對近壁面區域有2種處理方式：① 采用低雷諾數k-ε模型來直接求解黏性影響比較明顯的黏性底層和過渡層區域；② 不直接求解該區域，而是應用壁面函數法，即用一組半經驗公式將壁面上的物理量與湍流核心區內的相應物理量聯系起來。采用低雷諾數k-ε模型時，因黏性底層和過渡層內的物理量變化大，需要劃分較為細密的網格才能滿足計算要求，計算成本較高。與前者相比，壁面函數法能夠處理各種不同壁面流動問題，且具有計算效率高和工程實用性強的優點。因此，在本文的研究中，對近壁面區域采用標準的壁面函數法[7]27-29。

4.5.2 控制方程的離散方法

對控制方程采取不同的離散方式將會產生不同的數值求解方法，根據離散原理的不同主要分為有限差分法、有限元法和有限體積法。有限差分法對復雜幾何體適應性較差，近年來已經逐漸被有限元法和有限體積法代替。有限元法相對有限差分法，能夠處理復雜的幾何邊界條件，在固體力學的仿真計算中使用較多，但在流體力學計算中應用極少。有限體積法不僅具有有限差分法良好的守恒性，而且能夠和有限元法一樣，處理復雜的邊界條件，在流體力學的仿真計算中有著良好的適用性[7]29。ANSYS Fluent 14.5就是使用有限體積法來離散Navier-Stokes方程的。

4.5.3 SIMPLE算法

ANSYS Fluent 14.5中包括3種壓力-速度耦合算法：SIMPLE算法、SIMPLEC算法和PISO算法。前2種主要應用于穩態問題計算，PISO算法在用于計算瞬態問題時具有一定的優勢。在工程實際中，SIMPLE算法一般用于不可壓縮流體的仿真計算，經實踐檢驗是一種求解流體力學中流動問題的十分成功的算法之一。SIMPLEC算法在本質上與SIMPLE算法相同，理論上相當于采用不同的松弛因子的效果，故只要在SIMPLE算法中采用合適的松弛因子，即可達到與其他算法相同的收斂速度。因此，本文在數值模擬過程中選用SIMPLE算法來求解速度場與壓力場的耦合[7]30-31。

5 各項設置

① 模型設置

應用ANSYS Fluent 14.5中的離散相模型，開啟Erosion/Accretion物理模型。計算過程中，對控制方程組的離散采用有限體積法，擴散項采用二階迎風差分格式，壓力-速度耦合采用SIMPLE算法，湍流模型采用RNGk-ε雙方程，利用拉格朗日法對通過流場的顆粒進行逐個追蹤。

② 邊界條件設置

進口設置為速度進口(velocity-inlet)，出口設置為自由出流(outflow)，即在出口處的流動為充分發展的，各個變量(壓力除外)沿流動方向的梯度為0，離散相均設置為逃逸(escape)，壁面設置為無滑移壁面。

③ 其他設置

節流閥的規格為DN 50 mm。

進口處流體的速度為5 m/s，壓力為1.1 MPa，常溫輸送。整個模型重力場加速度為9.8 m/s2。

節流閥的材料采用碳素鋼，碳素鋼密度為7 850 kg/m3，碳素鋼法向反彈系數en的各項取值[7]24為0.993、-0.031、4.75×10-4、-2.61×10-6，碳素鋼切向反彈系數et的各項取值[7]24為0.998、-0.029、6.43×10-4、-3.56×10-6。

砂粒質量流量為0.000 5 kg/s，砂粒密度為1 500 kg/m3，砂粒直徑為150 μm，砂粒形狀系數為0.53，砂粒直徑函數的取值[7]27為1.8×10-9，速度分量函數的取值[7]27為2.6，沖擊角度函數的取值[7]27見表1。

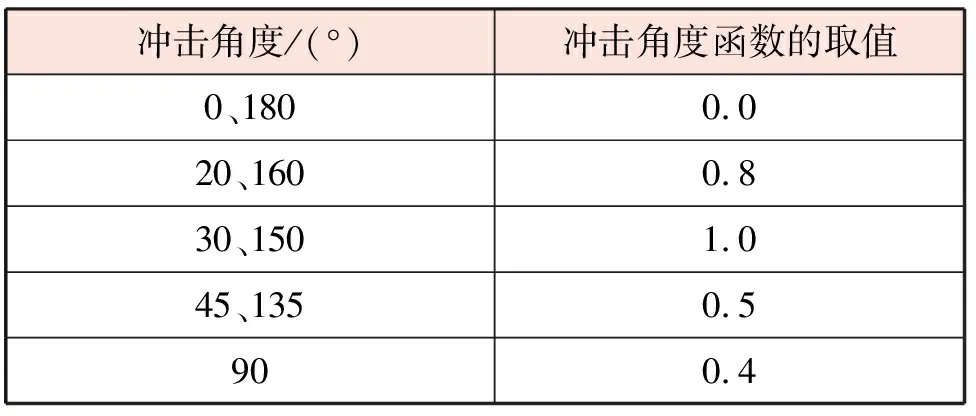
表1 沖擊角度函數的取值

本文假定天然氣介質為不可壓縮流體且流動是穩態的，天然氣的主要組分是甲烷，因此，模擬時連續相選擇甲烷，與甲烷有關的ρ、μeff等參數取系統默認值；Prk、Sk、Prε、C1ε、C2ε、C3ε、Rε、Sε等其他相關參數取系統默認值。

6 求解

求解控制參數：ANSYS Fluent 14.5基于有限體積法對控制方程進行離散和求解，在Solution Methods中，壓力速度耦合選擇SIMPLE。Gradient選擇Least Squares Cell Based，Pressure選擇Second Order，Momentum、Energy、Diffusive Phase均選擇Second Order Upwind。

亞松弛因子：在Solution Controls 中，Pressure、density、Body Force分別取0.3、1、1，Momentum、Energy分別取0.7、1。

殘差設定：Energy為10-5，其他均為0.001。

初始化：初始化方法選擇Standard Initialization，選擇Initialize從進口端面開始計算，經過迭代計算，得到結果。

7 模擬結果分析

7.1 錐形節流閥模擬結果分析

錐形節流閥沖蝕速率云圖見圖7，圖7中的色標右面的標值為沖蝕速率的數值，相應的單位為mg/(cm2·a)。

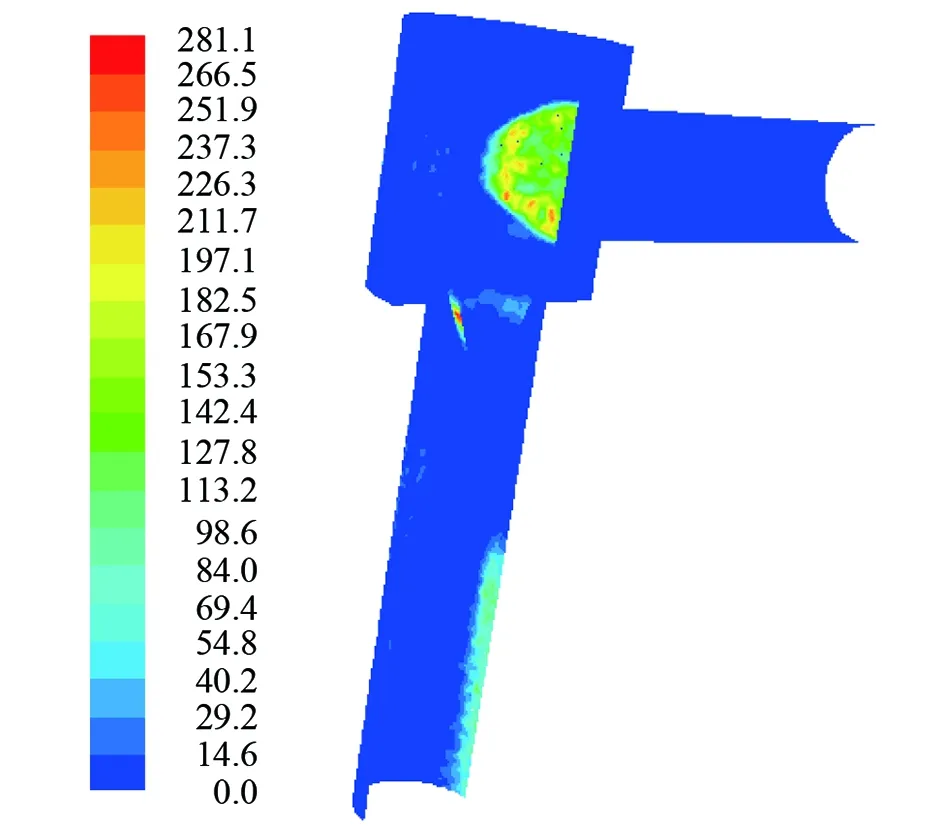
圖7 錐形節流閥沖蝕速率云圖(軟件截圖)

由圖7分析可知，錐形節流閥內部產生沖蝕的具體位置分為3個部分：①閥芯迎流壁面處，呈半橢圓狀區域，沖蝕速率相對較大；②閥芯與節流孔交接處，呈圓環狀區域，其中，在背對閥芯迎流壁面的一側靠近yOz平面的節流孔位置附近沖蝕速率最大；③出口管段內壁面處，呈長條狀區域，沖蝕速率相對較小，沖蝕區域面積較大。

綜合分析以上3個沖蝕位置，本文將出口管段作為沖蝕控制的主要區域，其主要原因包括以下3個方面：①出口管段的沖蝕面積較大，更需要加以控制；②通過采取改進閥芯結構的方式，容易實現對出口管段的沖蝕控制；③雖然閥芯迎流壁面處和閥芯與節流孔交接處的沖蝕速率均比出口管段內壁面處大，但是這兩處的沖蝕不可避免，故本文不做研究。

錐形節流閥粒子跡線圖見圖8，圖8中的色標右面的標值為砂粒編號的數值，以圖8中編號為第5 900號的砂粒的跡線為例，其顏色為紅色，由進口至出口構成其完整的運動軌跡。

圖8 錐形節流閥粒子跡線圖(軟件截圖)

將圖8中砂粒跡線與壁面相交的位置與圖7中的沖蝕位置相對比，兩者的位置基本一致，因此，砂粒跡線與壁面相交的拐點即為沖蝕點，由此可以判定沖蝕產生的原因主要是氣體攜帶的砂粒不斷沖擊和切削壁面所致。

由圖8分析可知，砂粒與閥芯迎流壁面碰撞反彈后，在背對閥芯迎流壁面處產生一定的積聚，積聚后的大量砂粒經節流孔處yOz平面兩側位置進入出口管段，在背對閥芯迎流壁面的一面靠近yOz平面的節流孔位置附近，砂粒與閥芯壁面接觸的相對速度和頻率比其他位置都大，因此，在該位置產生的沖蝕速率最大。

以下圖9～16，類似的云圖中關于色標標值的含義和單位分別與圖7和圖8一致。

7.2 圓臺狀閥芯錐形節流閥模擬結果分析

圓臺狀閥芯錐形節流閥沖蝕速率云圖見圖9，粒子跡線圖見圖10。

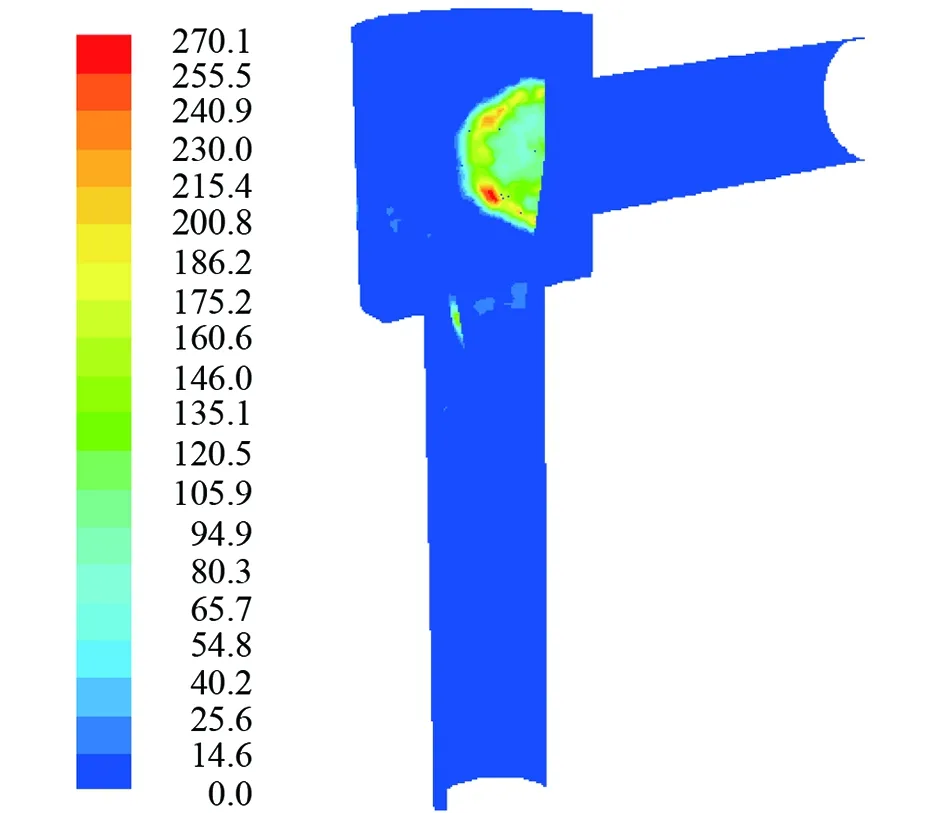
圖9 圓臺狀閥芯錐形節流閥沖蝕速率云圖(軟件截圖)

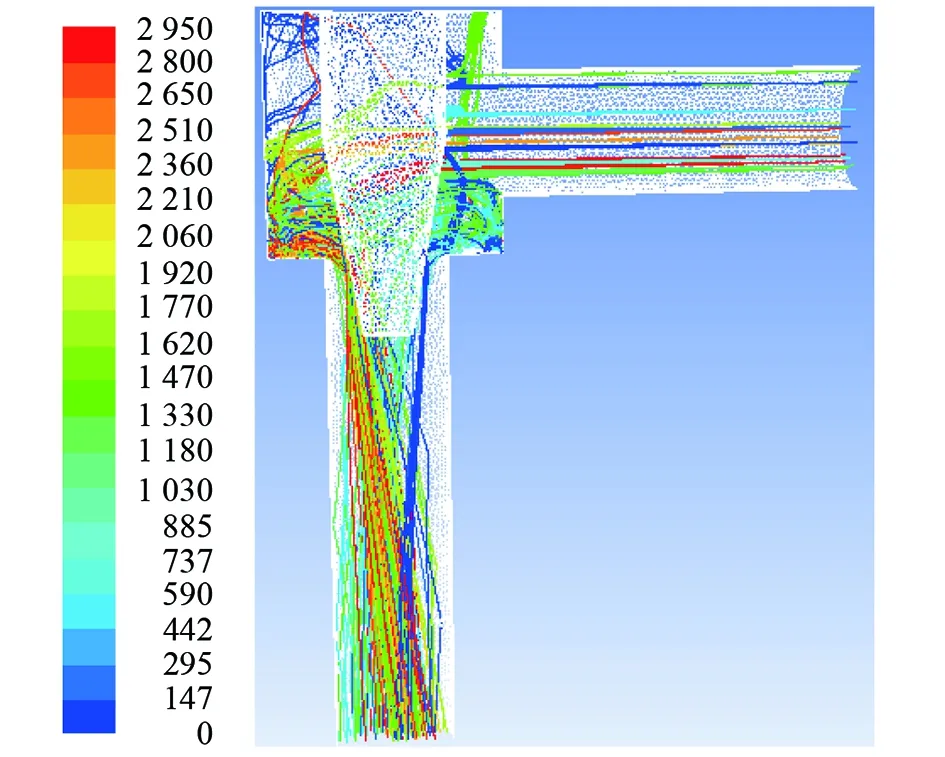
圖10 圓臺狀閥芯錐形節流閥粒子跡線圖(軟件截圖)

由圖9分析可知，閥芯迎流壁面處和閥芯與節流孔交接處產生沖蝕，出口管段基本無沖蝕破壞。與圖7相比，出口管段的沖蝕得到明顯改善。

由圖10分析可知，經節流孔后砂粒的軌跡受到閥芯結構改變的作用順勢向下，只有少數的砂粒碰撞到壁面，避免了出口管段內壁面受到較大沖擊。

圖9、10證明了改進后的閥芯結構既能夠滿足節流效果，又能夠針對出口管段起到一定減緩沖蝕的作用。

7.3 楔形節流閥模擬結果分析

楔形節流閥沖蝕速率云圖見圖11，粒子跡線圖見圖12。

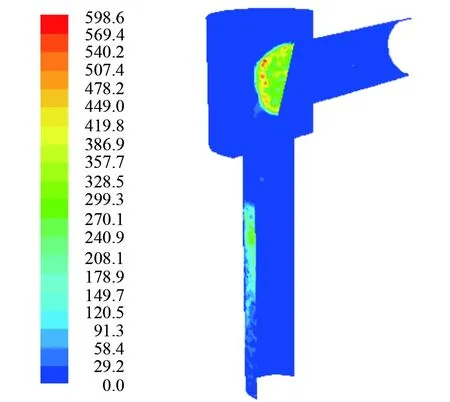
圖11 楔形節流閥沖蝕速率云圖(軟件截圖)

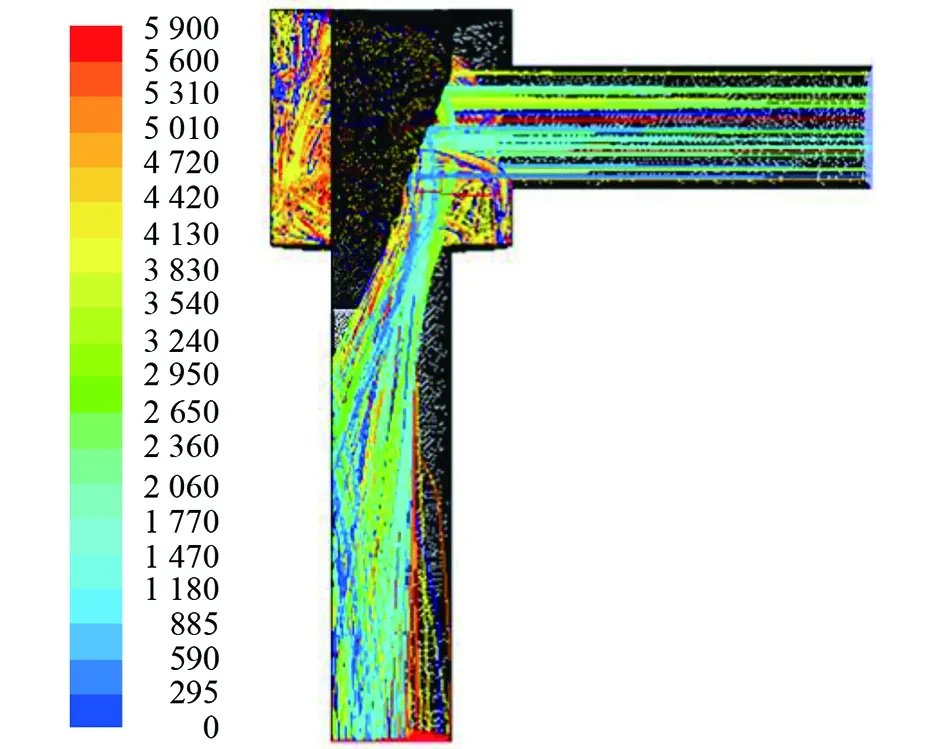
圖12 楔形節流閥粒子跡線圖(軟件截圖)

由圖11、12分析可知，楔形節流閥內部產生沖蝕的具體位置為閥芯迎流壁面處和出口管段內壁面處；最大沖蝕速率發生在閥芯迎流壁面處，是由砂粒與閥芯迎流壁面相碰撞產生較大的沖擊和切削作用所致；砂粒在與閥芯壁面碰撞反彈后直接進入出口管段，在節流孔處無沖蝕破壞，在出口管段內壁面處產生的沖蝕區域較大。

7.4 圓臺狀閥芯楔形節流閥模擬結果分析

圓臺狀閥芯楔形節流閥沖蝕速率云圖見圖13，粒子跡線圖見圖14。

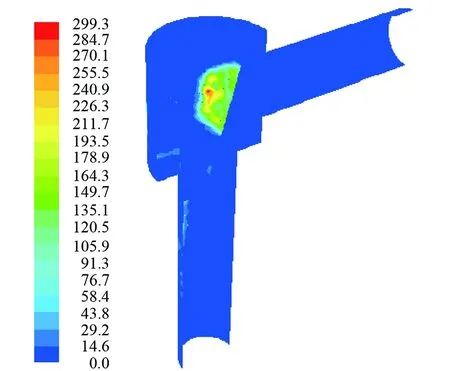
圖13 圓臺狀閥芯楔形節流閥沖蝕速率云圖(軟件截圖)

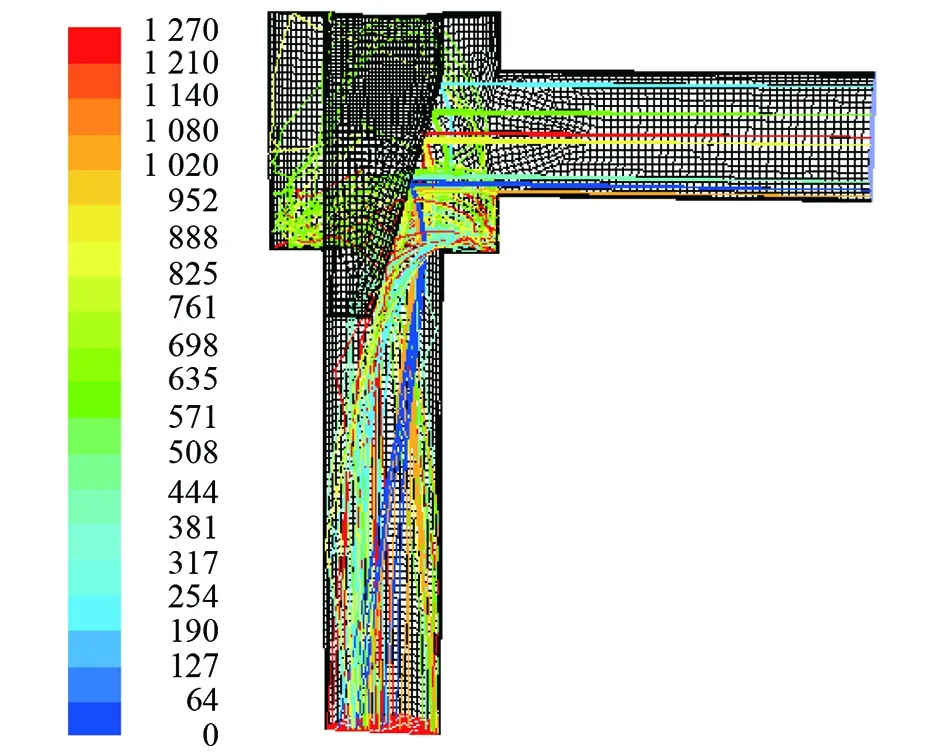
圖14 圓臺狀閥芯楔形節流閥粒子跡線圖(軟件截圖)

由圖13分析可知，產生沖蝕的主要區域為閥芯迎流壁面處，該處的沖蝕速率最大，與圖11的沖蝕情況基本一致，證明了閥芯迎流壁面處受到的沖蝕是不可避免的。

由圖14分析可知，該閥芯結構能夠為氣流及砂粒提供一定的導向作用，經過節流孔后砂粒的軌跡發生了部分改變，對出口管段內壁面的沖擊變小。

與圖11相比，出口管段的沖蝕區域和沖蝕速率都明顯變小，節流閥出口管段的沖蝕得到了一定的控制。

7.5 三段式閥芯楔形節流閥模擬結果分析

三段式閥芯楔形節流閥沖蝕速率云圖見圖15，粒子跡線圖見圖16。

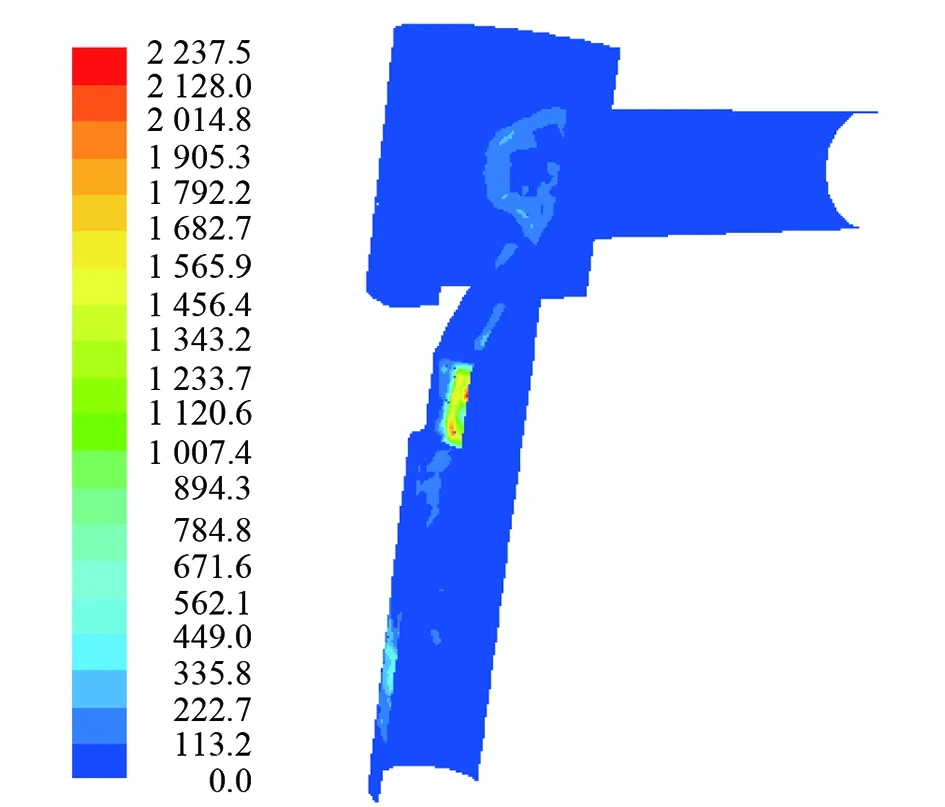
圖15 三段式閥芯楔形節流閥沖蝕速率云圖(軟件截圖)

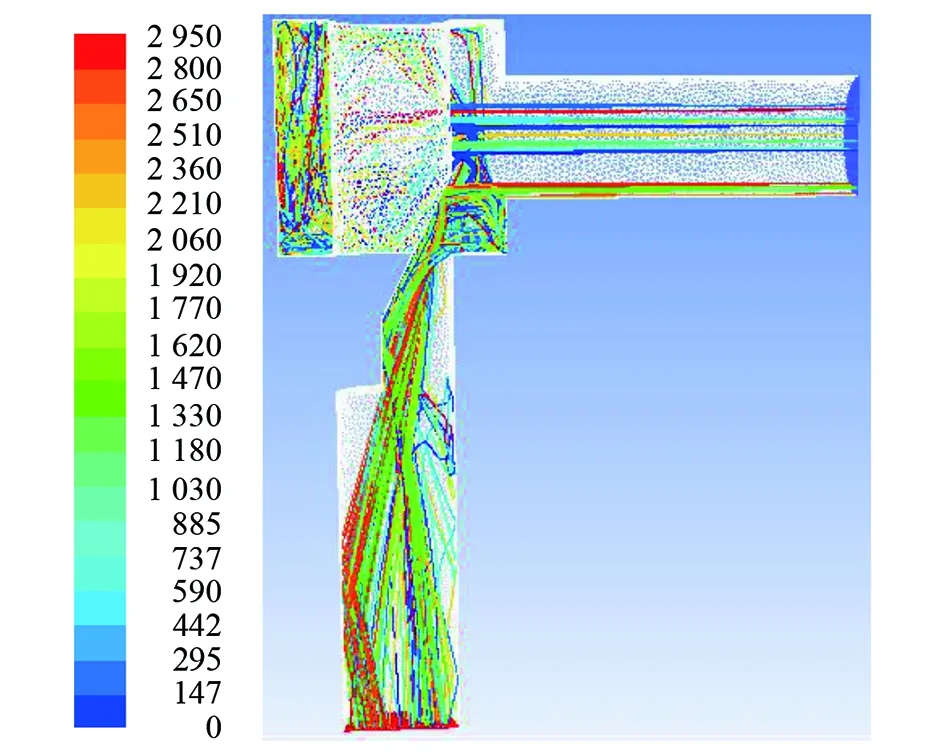
圖16 三段式閥芯楔形節流閥粒子跡線圖(軟件截圖)

為了方便模擬結果的分析，現將三段式閥芯楔形節流閥的閥芯結構分為上、中、下三段，其中，閥芯上部圓柱段為閥芯上段，閥芯中部與閥芯中軸線斜交段為閥芯中段，閥芯下部與閥芯中軸線平行段為閥芯下段。由圖15、16分析可知，沖蝕速率最大的位置為閥芯下段，主要是由于閥芯下段改變了砂粒的軌跡，此處壁面受到的沖擊和切削作用最大，故沖蝕速率也最大；與此同時，閥芯下段對節流效果影響較小，故實現了沖蝕破壞向對節流效果影響較小區域位置的轉移；由于三段式閥芯結構避免了大量砂粒直接沖擊出口管段內壁面，使得出口管段內壁面的沖蝕速率減小，起到了減緩沖蝕的作用。

另外，三段式閥芯楔形節流閥還能夠彌補楔形節流閥不易改變砂粒流向以及圓臺狀閥芯楔形節流閥節流效果差的缺陷。

8 沖蝕的預防和減緩措施

為了預防和減緩沖蝕破壞的發生，在設備構件本身因素方面，除本文中提出的改進閥芯結構的方法外，還可以在閥芯迎流壁面處采用耐沖蝕的材料、涂層保護以及加裝硬質合金套等措施，以提高閥芯的強度和耐磨度來減緩沖蝕。

對于節流閥出口管段內壁面的沖蝕破壞，可以通過結構上的改進來控制。目前最常用的方法是安裝防沖刺短節[8]，用防沖刺短節替代出口管段，在防沖刺短節入口段加裝硬質合金套，加大防沖刺短節的中段腔室，在防沖刺短節出口處加裝硬質合金套球頭[9]。

在流動介質因素方面，可以采取適當措施減少砂粒的含量。

在人為因素方面，關停和再啟動時應注意保持平穩性，不斷更新升級檢測設備，加大檢測頻率，及時發現問題，及時更換，加強預防。

9 結論

① 在氣-固兩相流條件下，節流閥內部的沖蝕破壞不可避免。

② 節流閥內部產生沖蝕破壞的位置為閥芯的迎流壁面處、閥芯與節流孔交接處以及出口管段內壁面處，軟件模擬結果與現場沖蝕失效情況一致。

③ 3種改進后的閥芯結構在一定程度上均改變了砂粒的運動軌跡，減小了對出口管段內壁面的沖蝕，對節流閥沖蝕控制的主要區域起到一定的保護作用。

④ 除采取改進閥芯結構的方法外，還可以通過采用耐沖蝕材料、涂層保護、加裝硬質合金套、加裝防沖刺短節等措施減緩節流閥內部的沖蝕破壞。