較大管徑合流三通局部阻力系數模擬計算
陳佑乾, 崔旭陽, 楊 迪, 雷萬寧,黃 濤, 白 超, 高 琳, 楊俊紅
(1.西安瑞行城市熱力發展集團有限公司,陜西西安710021;2.中低溫熱能高效利用教育部重點實驗室(天津大學),天津300350)
1 概述
三通被廣泛應用于供熱工程的管網系統中。流體在三通內流動時,管壁附近會形成分離區,流體沖擊擠壓等現象易造成局部流動壓力損失和能量耗散[1],直接影響設備的選型、能耗和運行成本[2],三通管結構和應力不連續的區域也會出現疲勞損傷[3]。因此,研究三通內流體的壓力損失對于管道系統的設計分析[4]和流體的安全有效輸送具有重要的意義。
國內外學者對流體通過三通產生的壓力損失流動特性進行了試驗與模擬研究[5-7]。對于三通的模擬,廣泛使用的是計算流體動力學(CFD)k-ε湍流模型[8]、大渦(LES)湍流模型[9]等。已有研究表明,三通的交匯角(側支管與直支管夾角)、流量比、面積比等因素對三通局部阻力具有較大影響[10-11]。不同結構參數、運行工況下,三通的局部阻力也有較大差別。受條件限制,試驗研究多針對DN 100 mm以下的三通,對DN 100 mm以上三通的試驗比較少。然而在供熱工程中,一級管網大多采用DN 400 mm以上的三通。本文采用Fluent軟件,分析主管雷諾數、分流比、管徑比、交匯角對合流三通局部阻力系數、三通內流體速度場的影響。
2 計算模型的建立
2.1 幾何模型及參數選擇
合流三通幾何模型見圖1,流體由直支管、側支管入口進入三通,經過合流處后從主管出口流出。直支管、側支管、主管的壓力及速度計算截面見圖1中面a-a、面b-b、面c-c。保持側支管公稱直徑為400 mm,改變直支管、主管公稱直徑,得到5種規格合流三通(尺寸參數見表1)。表1中,400×400×400表示主管公稱直徑的數值×側支管公稱直徑的數值×直支管公稱直徑的數值,相應的單位為mm,以此類推。
筆者選取主管流體流速、分流比、管徑比、側支管與直支管夾角4個影響參數進行分析,影響參數的變化范圍見表2。分流比q、管徑比d的計算式分別為:
式中q——分流比
qm,B——側支管質量流量,kg/s
qm,C——主管質量流量,kg/s
d——管徑比
dB——側支管內直徑,m
dC——主管內直徑,m
規格1~5合流三通對應的管徑比分別為1.00、0.80、0.67、0.50、0.38。為方便模擬,進行以下設定:認為內直徑等于公稱直徑。水溫度保持25 ℃恒定,忽略流體之間及流體與外界環境的傳熱。水始終充滿管子,管子中無氣相及固相介質存在。
2.2 湍流模型
考慮到流體流經三通合流處時的流動比較復雜,存在旋流及二次流,因此采用realizablek-ε湍流模型。該模型在模擬強逆壓力梯度、射流擴散率以及模擬分離、回流和旋轉時具有較高的精度。分別建立連續性方程、動量方程、湍動能方程、耗散率方程[12]。
2.3 邊界條件
直支管、側支管入口均為速度入口,水流方向垂直于入口截面。湍流定義方法選擇湍動能強度與水力直徑。主管出口采用自由出口邊界條件。設定計算域中全局表壓為0,因管徑較大,考慮重力影響,方向豎直向下,重力加速度為9.8 m/s2。管壁采用無滑移邊界條件,壁面粗糙度設定為0.045 mm。
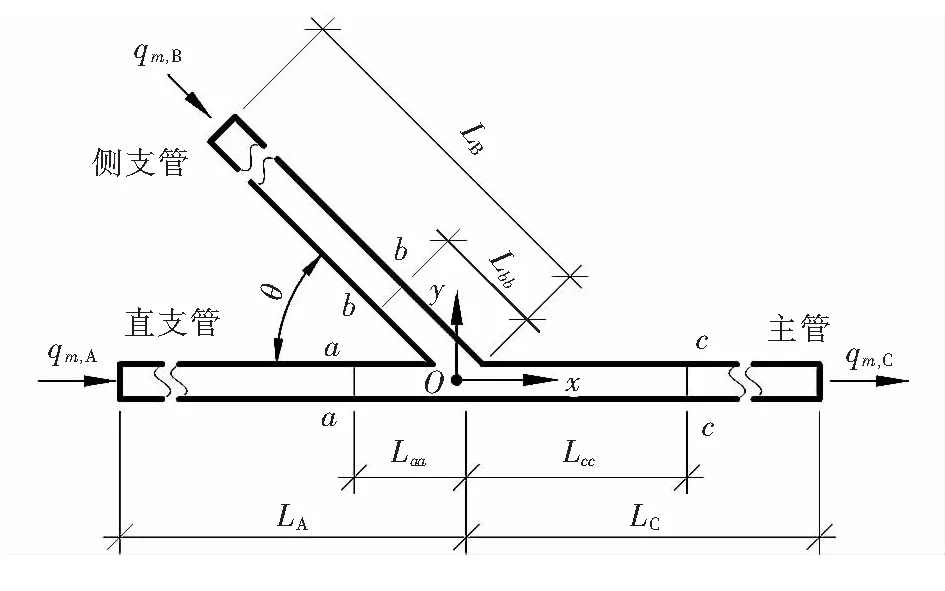
圖1 合流三通幾何模型
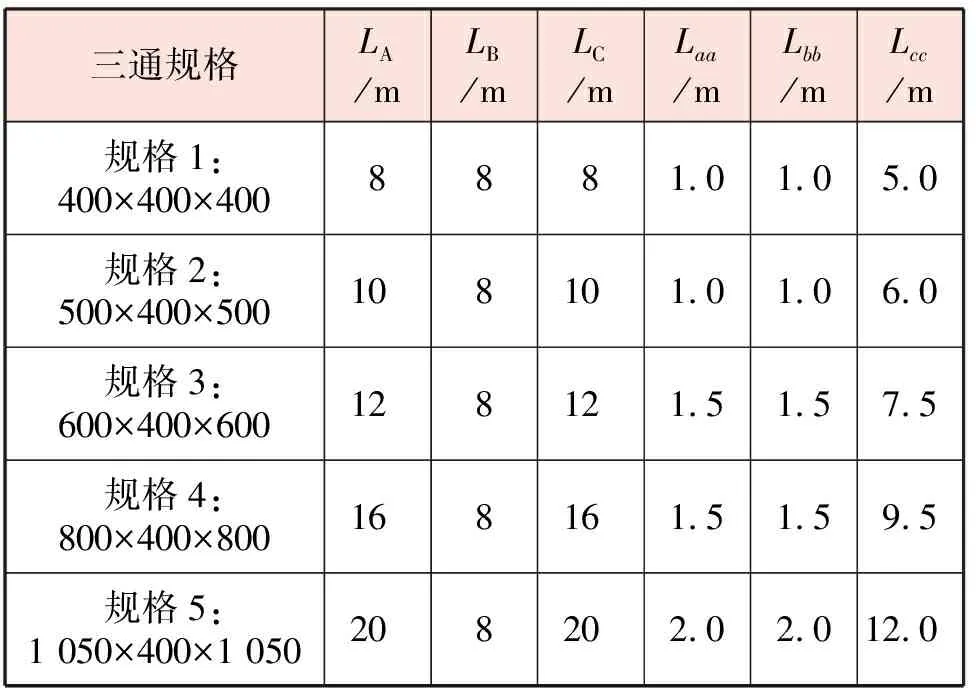
表1 5種規格合流三通的尺寸參數
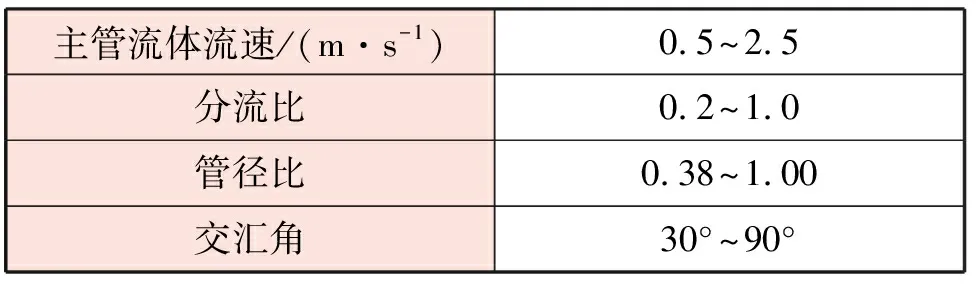
表2 影響參數的變化范圍
2.4 數值求解方法
建立三維模型,模型水平放置。本文研究穩定流動過程,因此采用穩態求解器進行模擬。在控制方程的離散化選項中,壓力項采用標準算法,動量方程及湍動能和耗散率方程均采用二階迎風格式離散,壓力和速度耦合采用SIMPLEC算法,收斂殘差值設置為10-4,迭代步長設置為2 000。
側支管與主管間局部阻力系數(即阻力系數1)ζBC、直支管與主管間局部阻力系數(即阻力系數2)ζAC的計算式為[13]:
式中ζBC——側支管與主管間局部阻力系數
pC、pB、pA——主管、側支管、直支管的平均靜壓,Pa
ρ——水密度,kg/m3,本文取998.2 kg/m3
uC、uB、uA——主管、側支管、直支管的平均流速,m/s
λC、λB、λA——主管、側支管、直支管的摩擦阻力系數
ζAC——直支管與主管間局部阻力系數
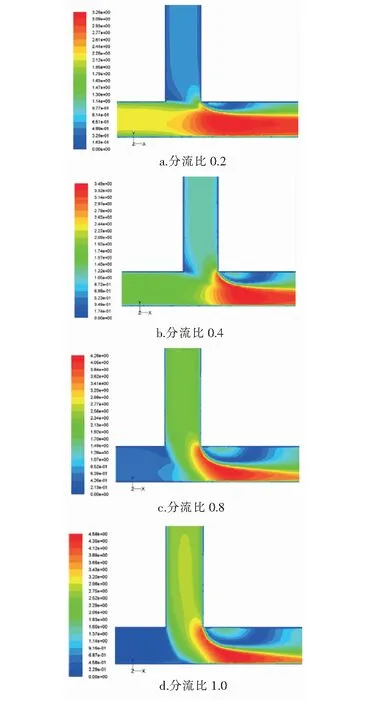
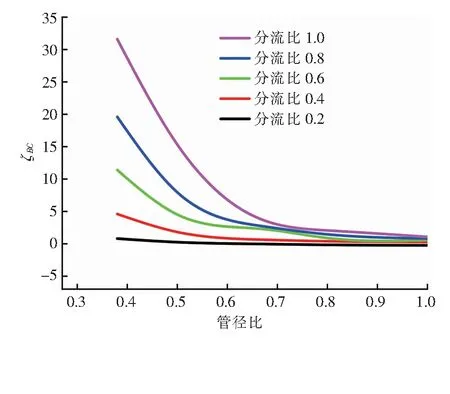
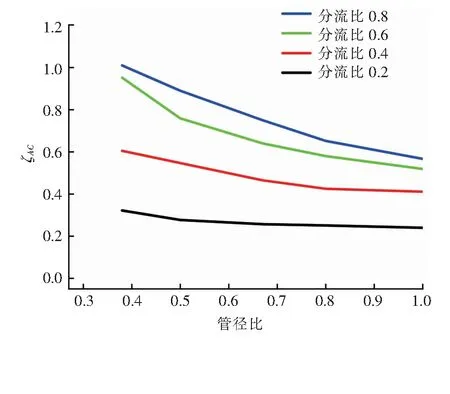
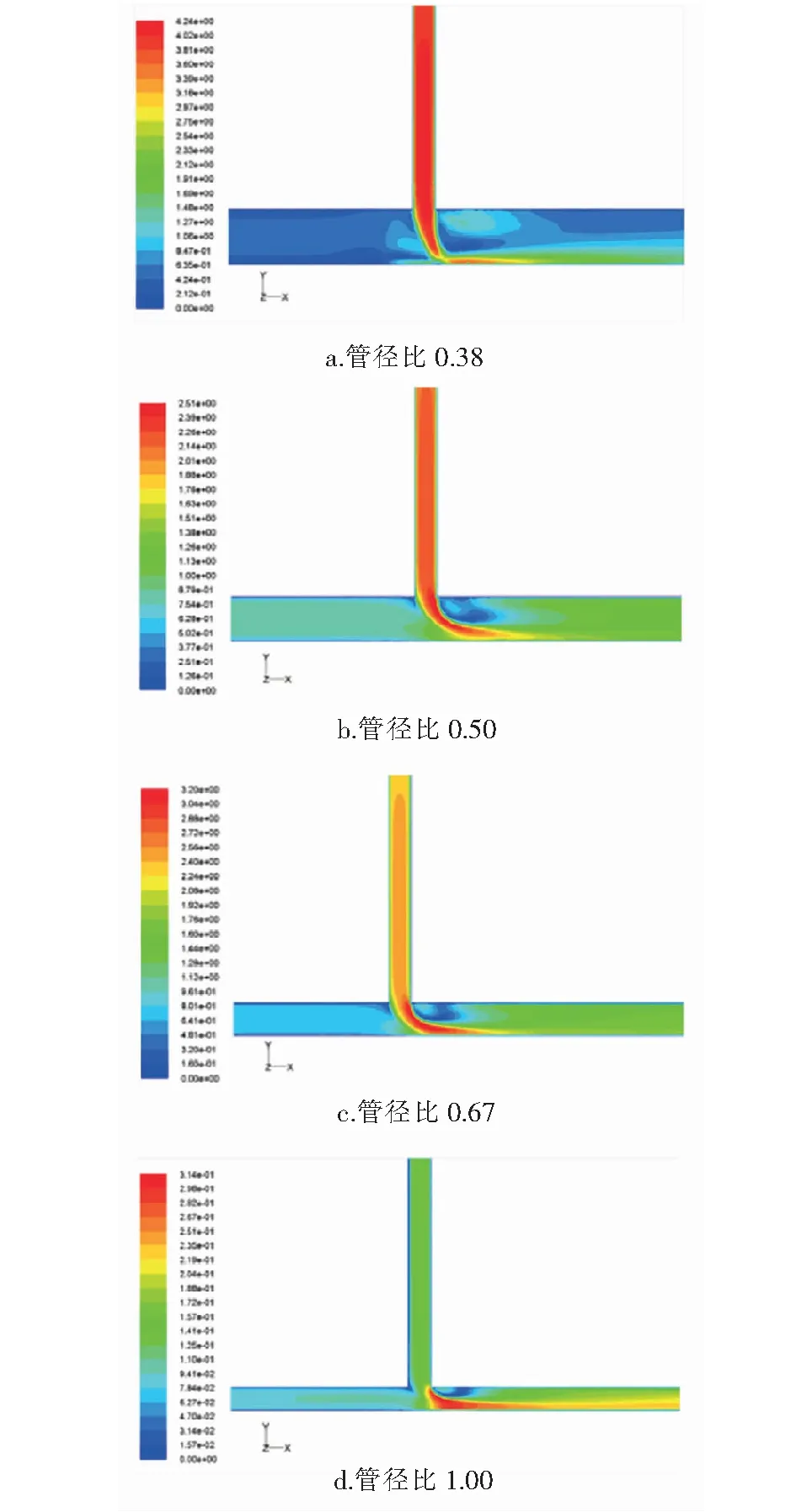
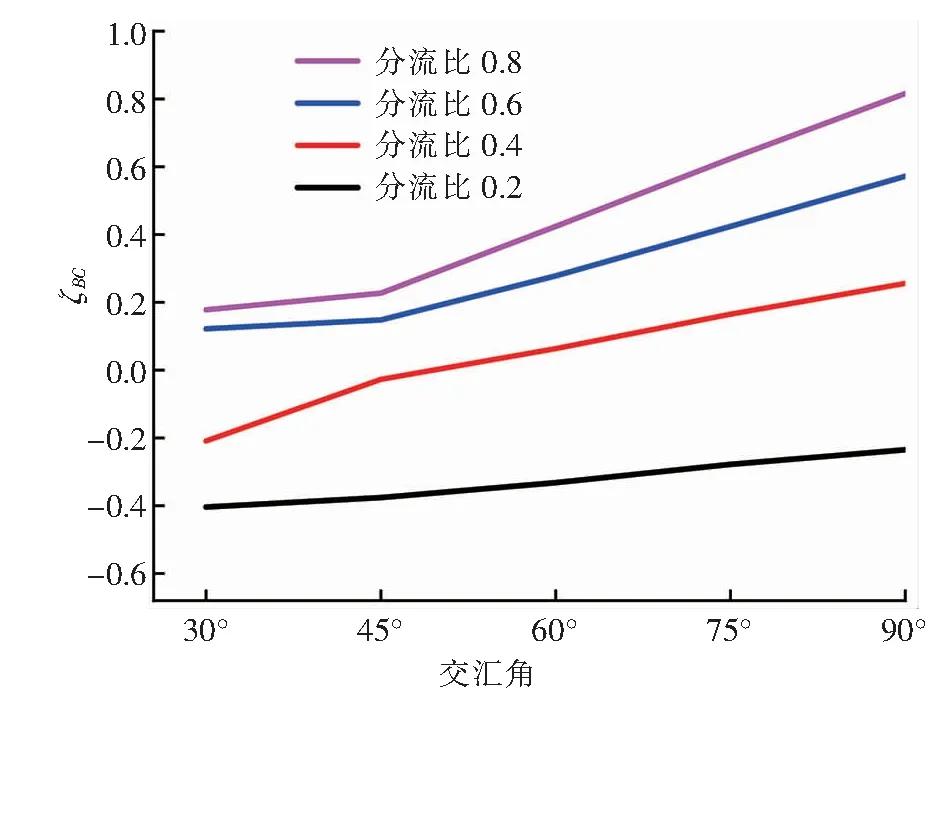
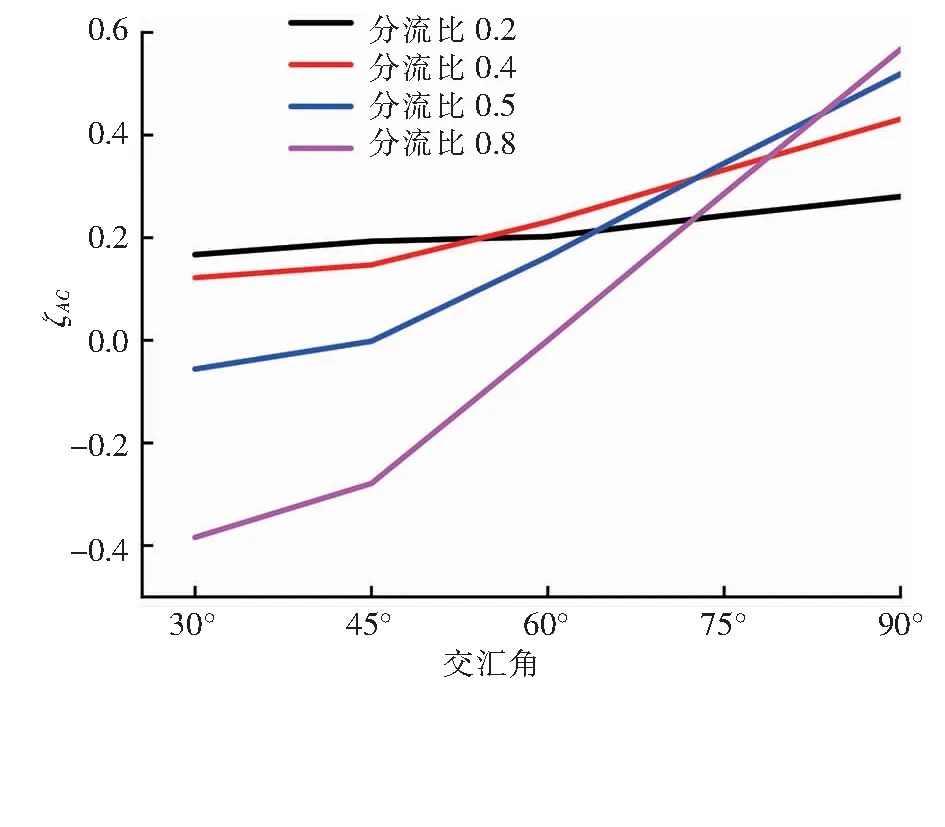
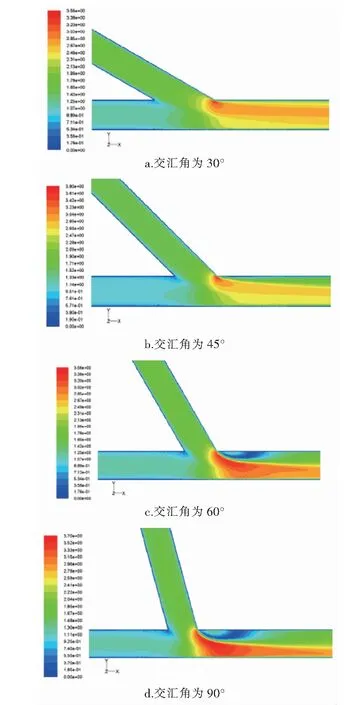
當4×103 λ=0.316 4Re-0.25 當1×105 λ=0.003 2+0.221Re-0.237 主管雷諾數Re的計算式為: 式中Re——主管雷諾數 ν——水的運動黏度,m2/s,取1×10-6m2/s 當主管雷諾數給定后,可計算得到主管平均流速,并根據分流比、管徑比可計算得到斜支管、直支管的進口流速。根據以上已知條件,由Fluent軟件模擬模型計算截面(水平中心截面)斜支管平均流速、直支管平均流速以及斜支管、直支管、總管平均靜壓,從而根據上述計算模型得到局部阻力系數1、2。 采用分塊劃分網格方法,在合流三通合流部分采用貼合性較好的六面體網格進行加密,其余位置采用四面體網格。主管水流速為2 m/s時,3種網格數量下(84 154、1 741 482、3 643 595),對規格1、T型三通(θ為90°)的ζBC隨分流比的變化進行模擬計算。由模擬結果可知,當網格數量為1 741 482時,ζBC的計算結果與網格數量為3 643 595時十分接近,比網格數量為84 154的計算精度高。因此,為兼顧計算精度與運算時間,網格數量最終選取1 741 482。 不同分流比規格1、T型三通的ζBC、ζAC隨主管雷諾數的變化分別見圖2、3。主管雷諾數2×105~106對應主管水流速范圍為0.5~2.5 m/s。 由圖2、3可知,當分流比一定時,當主管雷諾數大于4×105后,ζBC、ζAC基本不隨主管雷諾數的增大發生變化,即局部阻力系數進入阻力平方區,這與文獻[13]、[15]的研究結果基本一致。當主管雷諾數一定時,分流比越大,ζBC、ζAC均越大。 圖2 不同分流比規格1、T型三通的ζBC隨主管雷諾數的變化 圖3 不同分流比規格1、T型三通的ζAC隨主管雷諾數的變化 ζBC在分流比為0.2時出現了負值,而ζAC始終為正值。文獻[16]對這種情況進行了解釋:當兩股不同速度流體作湍流混合時,具有較大速度的流體損失一部分動能轉讓給速度較小的流體,前者的局部阻力系數為正值,后者的局部阻力有可能為負值(當其獲得的能量不足以克服混合時的能量損失時,也會出現正值)。因此,合流時兩分支的局部阻力系數有可能為一正一負,或者是都為正。 主管雷諾數8×105條件下,不同分流比規格1、T型三通截面速度分布云圖見圖4。由圖4可知,當分流比比較大時,特別是分流比為1.0時,在主管上部出現大范圍低速回流區,主管內出現明顯的速度梯度。當分流比比較小時,主管上部低速回流區明顯減小,主管內速度梯度不十分明顯。 主管雷諾數為8×105時,不同分流比T型三通的ζBC、ζAC隨管徑比的變化分別見圖5、6。由圖5、6可知,當分流比一定時,ζBC、ζAC均隨管徑比的增大而減小。管徑比越大,ζBC、ζAC的降幅越小,當管徑比大于0.8后,對二者的影響不再顯著。分流比越小,管徑比的影響越小。 主管雷諾數為8×105時,在分流比為0.6下,不同管徑比T型三通截面速度分布云圖見圖7。由圖7可知,當管徑比為0.38時,斜支管水流速比較高,三通內水流速分布很不均勻。管徑比越大,直支管、斜支管、主管的管徑越趨于一致,流速分布也更趨于均勻,主管上部的低速回流區也有所縮小。 主管雷諾數為106時,不同分流比規格1三通的ζBC、ζAC隨交匯角的變化分別見圖8、9。由圖8、9可知,當分流比一定時,ζBC、ζAC均隨交匯角的增大而增大。 主管雷諾數為106時,在分流比為0.6下,不同交匯角規格1三通的速度分布云圖見圖10。由圖10可知,隨著交匯角增大,主管上部低速回流區增大,出現了明顯的速度梯度。當交匯角減小時,主管上部低速回流區明顯減小,主管內速度梯度不十分明顯。 ① 主管雷諾數的影響:當分流比一定時,當主管雷諾數大于4×105后,阻力系數1、2基本不隨主管雷諾數的增大發生變化,即局部阻力系數進入阻力平方區。當主管雷諾數一定時,分流比越大,阻力系數1、2均越大。當分流比比較大時,特別是分流比為1.0時,在主管上部出現大范圍低速回流區,主管內出現明顯的速度梯度。 圖4 主管雷諾數8×105條件下不同分流比規格1、T型三通截面速度分布云圖(軟件截圖) 圖5 主管雷諾數為8×105時不同分流比T型三通的ζBC隨管徑比的變化 圖6 主管雷諾數為8×105時不同分流比T型三通的ζAC隨管徑比的變化 圖7 主管雷諾數為8×105時分流比為0.6下不同管徑比T型三通截面速度分布云圖(軟件截圖) 圖8 主管雷諾數為106時不同分流比規格1三通的ζBC隨交匯角的變化 圖9 主管雷諾數為106時不同分流比規格1三通的ζAC隨交匯角的變化 ② 管徑比的影響:當分流比一定時,阻力系數1、2均隨管徑比的增大而減小。管徑比越大,阻力系數1、2的降幅越小,當管徑比大于0.8后,對二者的影響不再顯著。分流比越小,管徑比的影響越小。當管徑比為0.38時,斜支管水流速比較高,三通內水流速分布很不均勻。管徑比越大,直支管、斜支管、主管的管徑越趨于一致,流速分布越趨于均勻,主管上部的低速回流區也有所縮小。 ③ 交匯角的影響:當分流比一定時,阻力系數1、2均隨交匯角的增大而增大。隨著交匯角增大,主管上部低速回流區增大,出現了明顯的速度梯度。 圖10 主管雷諾數為106時在分流比為0.6下不同交匯角規格1三通的速度分布云圖(軟件截圖)2.5 網格無關性驗證
3 模擬結果與分析
3.1 主管雷諾數的影響
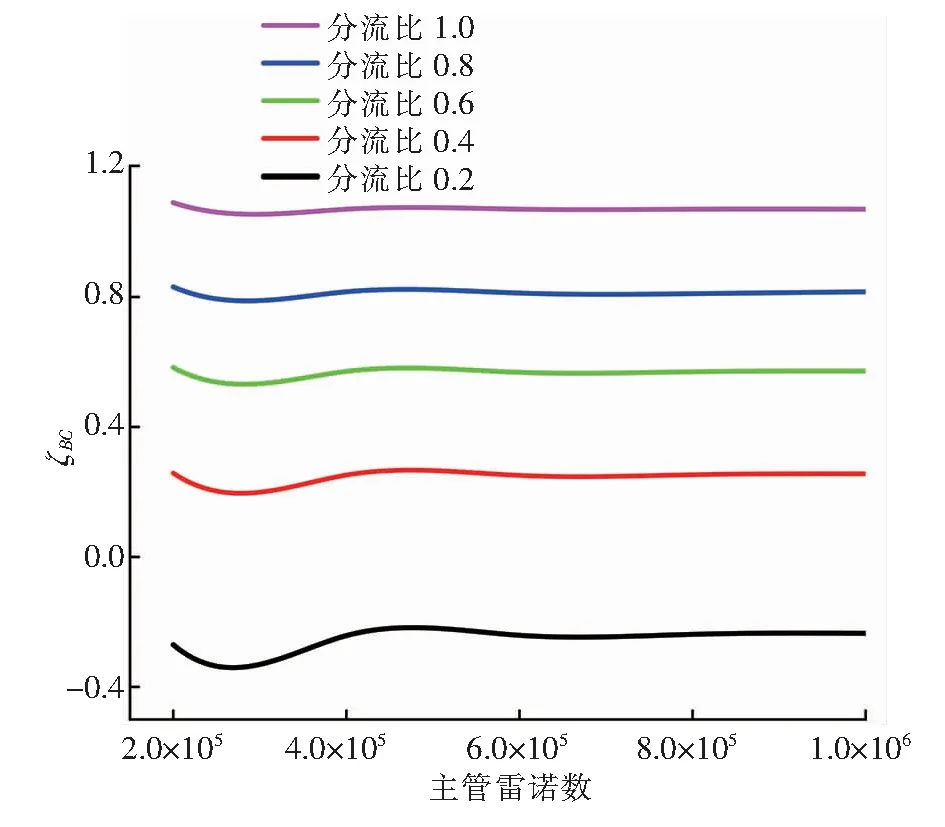
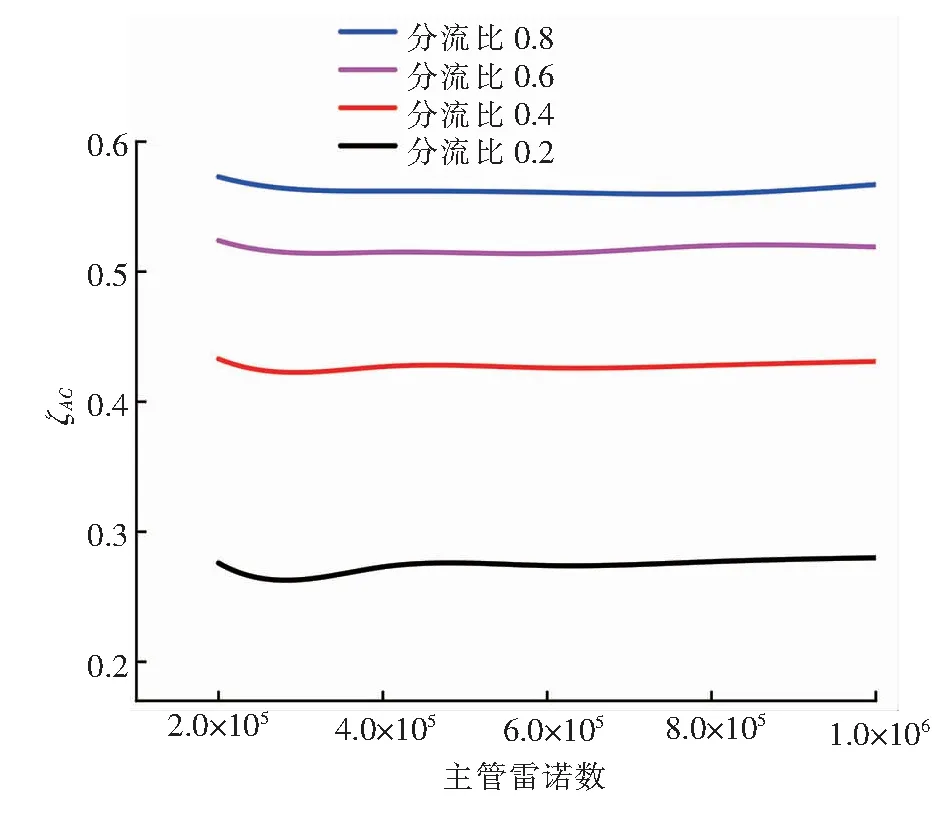
3.2 管徑比的影響
3.3 交匯角的影響
4 結論