機載高度表故障診斷的KPCA-BN方法

孫 擴，吳忠德，吳陽勇，吳昱舟

(海軍航空大學， 山東 煙臺 264001)

機載電子設備故障診斷往往會遇到很多未知性的問題。原因就在于測試對象的故障機理較為復雜、測試項目有限，以及提供的知識經驗不夠準確。針對歷史數據不完備、不確定性的問題，Pearl于1988年在概率推理和貝葉斯理論的基礎上提出了貝葉斯網絡，它適用于具有關聯測試屬性的故障診斷，是當前不確定性知識表達和推理方面最常見的診斷方法之一[1]。針對電網中故障不確定性和模糊性的特點，文獻[2]提出了基于故障區域識別和貝葉斯網絡的新型故障診斷方法。文獻[3]針對故障診斷領域中先驗信息缺乏的特點，提出了一種基于模糊貝葉斯網絡的故障診斷方法。文獻[4]針對故障診斷中的不確定或不完備信息，提出利用故障樹和鍵合圖結合共同構建貝葉斯網絡的故障診斷方法。

1 核主元分析及其特征降維

1.1 基于核函數的空間變換

基于核的方法在去除冗余信息、調整非線性數據結構所表現出的優良特性已被廣范應用并結合故障特征提取的其他方法中。最基本的原理就是通過引入核函數完成數據樣本特征空間的變化使原始數據線性可分，將特征空間的內積運算轉化為核函數的運算，減少了運算量[5-6]。空間的變換過程如圖1所示。

圖1 核空間變換過程

圖1中的xi，xj代表數據空間中的樣本點，以核函數為橋梁進行空間變換：

(xi,xj)→K(xi,xj)=〈φ(xi),φ(xj)〉

(1)

xi∈Rd(i=1,2,…,N)，Rd為數據樣本空間，該空間的維數是d，由Hilbert空間變換可知存在一個非線性映射φ把數據空間轉換為Hilbert空間，即φ∶Rd→H。選取核函數時應滿足Mercer條件，得到任意連續正定的核函數：

(2)

由式(1)、式(2)可以看出：在數據空間變換過程中核函數與特征空間的內積是等價的，因而只需要知道核函數的特征空間點內積，非線性映射φ的具體形式并不重要，只要根據故障特征的特點選擇合適的核函數即可。

1.2 核主元分析的基本原理

核函數主元分析法(KPCA)的基本原理是利用核函數的內積運算將非線性的數據樣本空間映射為線性的高維特征空間[7]，然后再用主元分析法(PCA)的算法進行故障特征分析并提取主元成分，將高維的特征空間投影為低維的數據樣本空間，以便對數據的聚類分析。

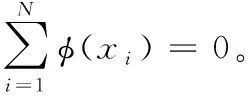
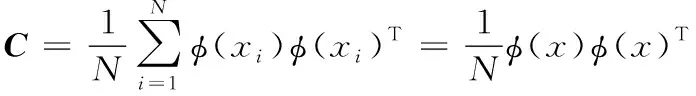
(3)

設協方差矩陣C的特征值為λ，特征向量為α，將協方差矩陣C特征值分解得到：

λα=Cα

(4)

定義一個核函數矩陣K滿足Mercer條件[8]：

K=φ(x)Tφ(x)

(5)

對核函數矩陣K進行特征值分解

λkαk=Kαk=φ(x)Tφ(x)αk

(6)

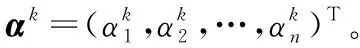
(7)

將特征向量ν單位化得

(8)

進而求得特征空間樣本φ(x)在特征向量ν上的投影，則樣本x的第k個非線性主元為

(9)

1.3 核主元分析算法的實現

KPCA算法的實現步驟如下：

步驟1 假定從數據空間中選取m組數據集，每組數據中包含n個特征屬性。構造出一個m×n維的數據樣本矩陣。

步驟2 選取合適的核函數。為了故障診斷和分類效果，此處選擇簡單可行的徑向基高斯核函數

步驟3 對核函數矩陣中心化，防止經過非線性映射后無法均值化；

步驟4 采用Jacobi矩陣計算式(6)中K的特征值和特征向量。

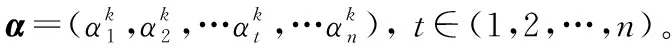
步驟6 計算協方差矩陣的主元貢獻率Bi并按由大到小順序排列有B1≥B2≥…≥Bt≥…Bn，i∈(1,2,…,n)，令Bt≥P，通常取P=85%，所以前t個特征值所對應的變量就是所需要提取的主元變量。

步驟7 計算數據在提取主元特征向量上的投影βi，i∈(1,2,…,t)。所得投影即為特征空間經KPCA降維處理后的數據。

2 貝葉斯網絡模型的故障定位

建立好網絡模型后，通過貝葉斯公式計算出故障模塊的最大后驗概率，實現故障的隔離定位。只討論單故障情況，即與每項測試相關聯的至多只有一個模塊發生故障。假定一個測試tj與m個模塊相關聯，則該測試的條件概率的個數就是對應相關模塊的個數m，記為Pdij。已知故障模塊si的先驗概率P(si)，所以測試項的故障全概率為

(10)

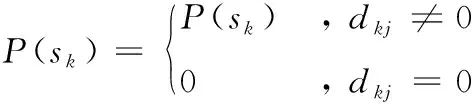
(11)

采用貝葉斯公式計算測試檢測故障情況下模塊的故障后驗概率為

(12)

具體計算見第3節，通過計算可以得到測試tj所對應的m個模塊的故障后驗概率，并通過比較得出單個測試特征的故障模塊最大后驗概率最優估計值為

(13)

假設貝葉斯網絡模型內共有n個測試狀態，計算后會產生n個有關故障模塊的最大后驗概率，而這n個值并不完全是同一測試故障狀態下得到的，所以在單故障條件下無法定位故障模塊的位置，引起“匹配沖突”的問題。

為解決“匹配沖突”引入屬性加權規則。屬性加權的基本原理，是在各個測試屬性的基礎上，乘上一個權值，來對不同屬性特征帶來的影響加以區分。由于各模塊的最大后驗概率是針對不同測試屬性條件而言的，我們定義一個可靠性因子α作為加權項，即α=P(tj)。則有關聯屬性加權后的公式為

(14)

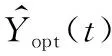
3 基于KPCA-BN的故障診斷模型

KPCA-BN診斷模型首先采用KPCA對故障數據進行特征降維處理，然后再將所得數據輸入貝葉斯網絡中進行故障診斷。將KPCA在處理冗余及非相關特征量的優點與貝葉斯網絡對不確定信息的故障分類優良特性相結合應用在故障診斷方面會有較好的效果[10]。該方法的故障診斷流過程如圖2所示。

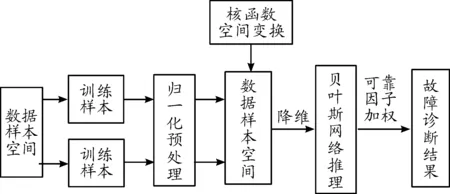
圖2 故障診斷流程

對診斷對象—某型高度表作為一個外場可更換單元(LRU，Line )，通過自動測試系統平臺及數據庫，應用KPCA-BN故障診斷方法，選取合適的故障模式和故障測試特征屬性，其故障—測試關聯表見表1。本文研究的某型機載高度表測量范圍為0～1 500 m，發射機發出的射頻信號載波頻率為4 300 MHz、脈沖重復頻率為10 kHz、功率為100 W的射頻信號，剩余的一部分進入距離計算器模塊作為時間基準信號使用。發射信號經過地面或水面的反射作為回波信號被接收機成功接收，經過一系列變換、放大、檢波等操作變為視頻回波脈沖信號進入距離計算器。將時間基準時間信號與視頻回波脈沖信號之間的時間間隔轉換為與真實高度成正比的直流電壓。

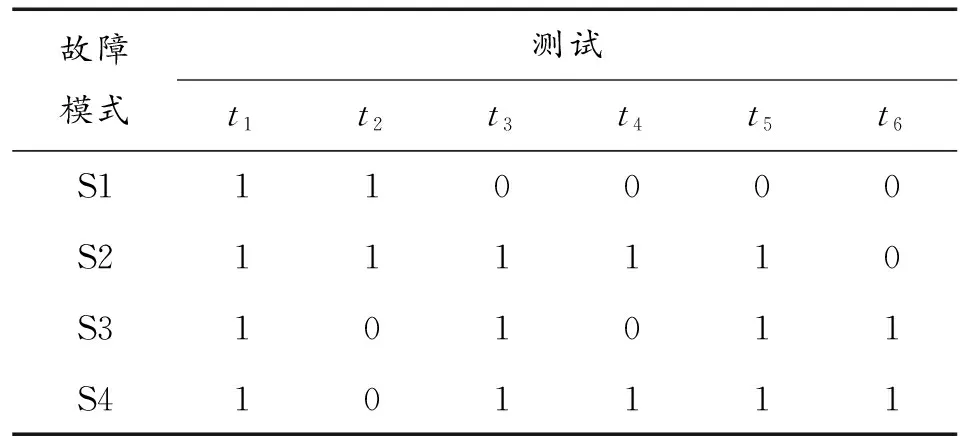
表1 高度表故障—測試關聯表

故障模式共有4種，分別為S1(穩壓電源模塊故障)、S2(發射機模塊故障)、S3(接收機模塊故障)和S4(距離計算器模塊故障)。故障測試特征屬性有6種，分別為t1(+5 V電壓測試)、t2(脈沖重復頻率測試)、t3(內部隔離度測試)、t4(外部距離電壓測試)、t5(模擬距離精度測試)和t6(零高度靈敏度測試)。表中主體部分數字“1”代表模塊與測試間有關聯，“0”則代表無關聯。

4 應用實例分析

在數據庫和知識庫中選取穩壓電源模塊、發射機模塊、接收機模塊、距離計算器模塊等4個模塊所對應的故障訓練數據集是4×48=192組。測試數據集樣本也是192組，見表2。

表2 高度表樣本數據集

在192組數據集中對應4個模塊，包含6個測試特征屬性。采用訓練樣本對貝葉斯網絡進行推理訓練，然后將通過核主元分析法降維的測試樣本的特征向量輸入訓練好的貝葉斯網絡中實現故障診斷與分類。核函數與核參數的選擇對數據的特征選取非常重要。經過試驗比對，選擇徑向基高斯函數作為核函數，取核參數σ=0.8。

在6維的測試特征空間中，前3個測試特征向量的累積貢獻率>85%，故通過PCA和KPCA對數據特征降維處理后得到三維特征空間投影效果，見圖3和圖4。

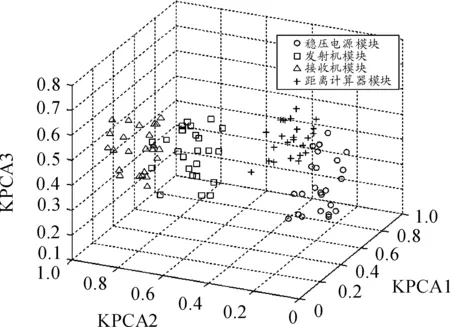
圖3 PCA處理數據三維特征投影

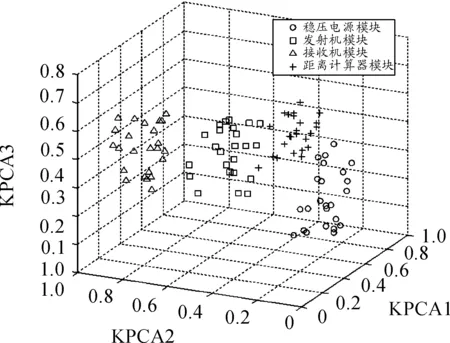
圖4 KPCA處理數據三維特征投影

通過圖3和圖4的比較可以看出：PCA和KPCA兩種特征選取方法都壓縮了試驗數據量，對數據都有一定的聚類效果。但是對比可以發現，PCA處理過的故障模式下的數據樣本中，如s1和s4、s2和s3樣本數據之間有些許的重疊，而KPCA處理的數據樣本基本沒有重疊，可分性好。結果表明：KPCA采用核函數特征空間變換由非線性數據空間映射為低維空間相比PCA有更好的效果。

根據表1可以建立相應的基于測試特征的貝葉斯網絡模型，見圖5。根據機載高度表的有關專家先驗知識及數據庫歷史測試數據統計計算，可以得到故障模塊的先驗故障概率及故障的條件概率。這里取模塊的先驗故障概率P(s1)=0.23，P(s2)=0.27，P(s3)=0.19，P(s4)=0.31，其故障的條件概率為：P(tj|si)(i=1,2,3，4,j=1,2,…,6)，見表3。

圖5 基于測試特征的貝葉斯網絡模型

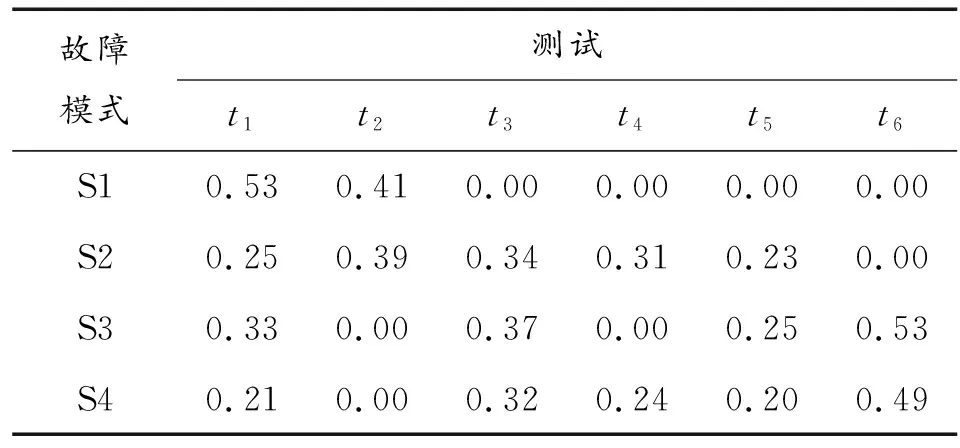
故障模式測試t1t2t3t4t5t6S10.530.410.000.000.000.00S20.250.390.340.310.230.00S30.330.000.370.000.250.53S40.210.000.320.240.200.49

以圖5中的貝葉斯網絡模型圖5(a)為例，已知模塊s1的故障先驗概率及測試t1的條件概率Pd11、Pd21、Pd31、Pd41，由式(10)可得測試t1故障的全概率為

p(t1)=(t1|s1)·P(s1)·(1-P(s2))·

(1-P(s3))·(1-P(s4))+(t1|s2)·

P(s2)·(1-P(s1))·(1-P(s3))·

(1-P(s4))+(t1|s3)·P(s3)·

(1-P(s1))·(1-P(s2))·(1-P(s4))+

(t1|s4)·P(s4)·(1-P(s1))·

(1-P(s2))·(1-P(s3))

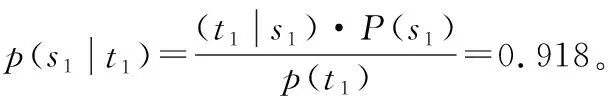
其他的測試的故障全概率及測試下各模塊的故障概率也同理可得。診斷測試故障全概率分別為0.133、0.150、0.145、0.112、0.095、0.193。測試下的最大后驗概率包括s1、s2、s4三個模塊，由于并不是同一測試狀態下的最大后驗概率，需要利用可靠性因子加權來判斷(表4)。代入式(14)中可得模塊s1、s2、s4對應的加權最大后驗概率分別是0.121 9、0.105 3、0.151 9。

所以可以得出結論是距離計算器模塊發生故障。上述基于測試的貝葉斯網絡故障診斷方法，可以通過運算得到最大后驗概率來判斷故障模塊及故障模式。貝葉斯網絡是針對不確定性故障診斷的主流方法之一，所以本文以貝葉斯網絡作為故障診斷的核心方法，將PCA和KPCA分別與貝葉斯網絡方法結合，并與基于測試的貝葉斯網絡方法[11]進行試驗對比。以特征維數、各模塊故障診斷準確率為評價指標對BN、PCA-BN和KPCA-BN三種推理機算法結果進行比較，見表4。KPCA-BN與PCA-BN相比較而言，加入核的方法增強了故障特征提取的特性，使得最終的故障診斷準確率提升了1.5%。

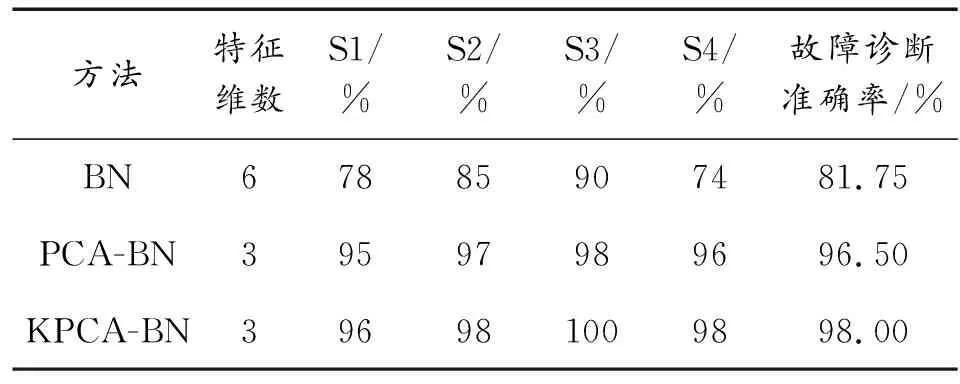
表4 三種方法故障診斷結果比較

通過主成分分析處理后，特征維數由6維降到3維，再將經KPCA處理的數據輸入基于測試的貝葉斯網絡中推理得到與單獨采用貝葉斯網絡方法相同的故障隔離結果，即距離計算器模塊故障，并且與實際故障模塊相一致。說明本文采用的改進方法確實有效。而且經過PCA和KPCA數據處理后，各個模塊的故障診斷準確率得到了大幅度提高。

5 結論

提出了通過核函數主元分析進行特征選取的貝葉斯網絡故障診斷研究模型。利用基于核函數的主元分析法對數據進行降維處理，實現了非線性高維數據樣本空間到低維的特征向量空間轉換。以某型機載高度表為研究對象進行基于測試的貝葉斯網絡模型構建，采用貝葉斯公式計算模塊的最大后驗故障概率，提出可靠性因子的概念，對后驗概率進一步修正，得出最終的故障診斷結果。以故障識別率、特征提取時間等指標作為評價標準，將本文中提出的KPCA-BN方法與PCA-BN和BN兩種方法對比，證明所提方法在故障診斷中的有效性。