雙模隨機交錯晶場對spin-1和spin-1/2混合自旋納米管中Blume-Capel模型磁化強度的影響

李曉杰,劉延春,李新軍

(齊魯理工學院，濟南 250200)

1 引 言

自1966年，Blume-Capel(BC)模型被創建之后[1,2]，人們已經利用不同方法對多種晶格上的BC模型的磁化性質、熱力學性質、磁滯回線和相圖進行了研究.Y.F.Zhang小組研究了外磁場和交換相互作用都遵循雙模隨機分布時，簡立方晶格中混合自旋系統的臨界行為[3].同年里，該小組又研究了外磁場遵循三模隨機分布時，簡立方晶格中混合自旋系統的相變行為[4].文獻[5]利用有效場理論研究了簡立方晶格中BC模型的補償行為和磁化過程.文獻[6]中研究了外磁場服從雙峰離散分布時蜂巢晶格的相變性質，發現外磁場、晶場和自旋間交換相互作用影響系統的相變并且系統出現重入現象；文獻[7]的研究表明稀釋晶場對蜂巢晶格系統磁學性質和相變的影響，結果顯示當晶場滿足稀釋分布時對系統的相變沒有影響并且系統不會出現三臨界現象.近幾年來，納米管漸漸成為磁熱性質研究領域的一個熱點，實驗與理論方面都已經取得一定的研究結果.實驗上，毛瑞等人以植物纖維素為模板，制備出了納米管狀SnO2材料，測試結果顯示，此SnO2納米管狀材料能夠提高鋰離子的擴散速率，有效解決解充電放電過程中電極材料體積膨脹問題[8].文獻[9]中發現Fe-Ni磁性納米管具有明顯的各項異性；理論上，Zaim小組研究了外磁場滿足三模分布時納米管上自旋為1Ising模型的磁性質和相圖[10]，結果表明該系統具有一階相變、三相臨界點和二階相變并出現重入現象.Osman等人分別討論了納米管中純自旋系統的磁化強度、磁化率、熱力學性質和相圖[11]，討論了晶場對系統磁熱性質的影響，結果顯示系統存在一階相變和二階相變.文獻[12]利用有效場理論研究混合自旋納米管系統的磁熱特性，結果顯示系統存在三臨界點.文獻[13]研究了Ising納米管系統中BC模型的磁滯行為.T.Kaneyoshi 討論了納米管系統中外殼層和內殼層最近鄰自旋間交換相互作用對磁化率的影響[14].文獻[15]顯示雙模隨機晶場中BC模型的磁化強度和相變性質，得到了系統的磁化強度與溫度和雙模隨機晶場的關系以及相圖，結果表明系統在雙模隨機晶場中會表現出不同的磁學性質和相變行為.文獻[16]討論了納米管上BEG模型的熱力學和相變性質，研究發現納米管系統存在三臨界點.文獻[17]研究了稀釋晶場作用下納米管中BC模型的磁化性質，結果表明，稀釋晶場作用下系統的內能、比熱和自由能呈現出不同的磁學性質.文獻[18]利用基于密度泛函理論的第一性原理方法研究了稀土金屬La吸附摻雜BN納米管的儲氫性能.據我們所知，迄今人們還沒有研究外磁場、晶場參數比值和雙模隨機交錯晶場對納米管系統平均磁化強度的影響.為了弄清楚外磁場、晶場參數比值和雙模隨機交錯晶場對納米管系統磁化性質的影響，本文利用有效場理論對納米管上混合自旋BC模型格點的平均磁化強度與雙模隨機交錯晶場取值概率、外磁場、晶場參數比值和晶場的關系進行了研究，給出了平均磁化強度隨溫度的變化曲線.

2 模型和方法

無限長納米管由內殼層和外殼層兩部分組成，見圖1.圖1(a)為納米管的立體示意圖，圖1(b)給出其橫截面示意圖.為了更清晰地顯示不同格點上具有相同配位數的磁性原子，用圓圈、方塊和三角形分別代表配位數為5、6和7的磁性原子.外殼層每個磁性原子的自旋為1，內殼層每個磁性原子的自旋為1/2.圖中原子間的連線代表最近鄰磁性原子之間存在交換相互作用，它們的大小分別為J1、J2和J.

圖1 納米管示意圖.(a) 立體圖，(b) 截面圖，圓圈和方塊代表外殼層磁性原子，三角代表內殼層磁性原子，實線表示最近鄰自旋間的交換相互作用.Fig.1 Theschematic pictures of nanotube:(a) perspective view of the cylindrical nanotube,(b) its cross section.The circles and squares respectively represent magnetic atoms at the surface shell.The triangles are magnetic atoms constituting the core shell.The bonds connecting the magnetic atoms represent the nearest-neighbor exchange interactions.

納米管上BC模型的哈密頓量可表述為

(1)

其中S=-1；σ=±1/2.J1代表外殼層最近鄰自旋間的交換相互作用，J2代表內殼層最近鄰自旋間的交換相互作用，J2代表外殼層和最近鄰的內殼層自旋間的交換相互作用，h代表外磁場，Di代表作用在格點i上的隨機交錯晶場，它們都滿足雙模晶場分布

P(Di)=pδ(Di-D)+(1-p)δ(Di-αD),

(2)

其中p(0≤p≤1)表示隨機晶場取值為D的概率，1-p代表示隨機晶場取值為αD的概率，α(-1≤α<0)為一無量綱參數，代表晶場強度的比值.當p=1或0時，含雙模交錯晶場的BC模型退化為含恒定晶場的BC模型.

利用有效場理論[19-21]可以得到外殼層格點自旋磁化強度m1和m2，內殼層格點自旋磁化強度mc的自洽方程：

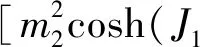
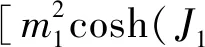
(3a)

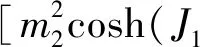
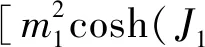
(3b)

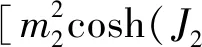
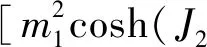
(3c)

其中函數F(x)定義為

=pf(x,D)+(1-p)f(x,αD),

(4)

(5)

函數f(x,Di)的表達式為

(6)

其中β=1/kBT，T是絕對溫度，kB是玻爾茲曼常數.另外，為了整體上描述系統的磁學性質可引入平均磁化強度[22]，它的定義為

(7)

3 結果與討論

為了便于研究，不特別說明，本文余下內容均取J1/J=J2/J=1.為了不失一般性，令外磁場h、晶場強度D和等效溫度kBT以J為單位，通過求解方程(3)，給出了雙模隨機交錯晶場作用下系統平均磁化強度隨溫度的變化曲線.

3.1 類對稱交錯晶場作用下，外磁場為零時，概率對系統平均磁化強度的影響

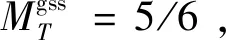
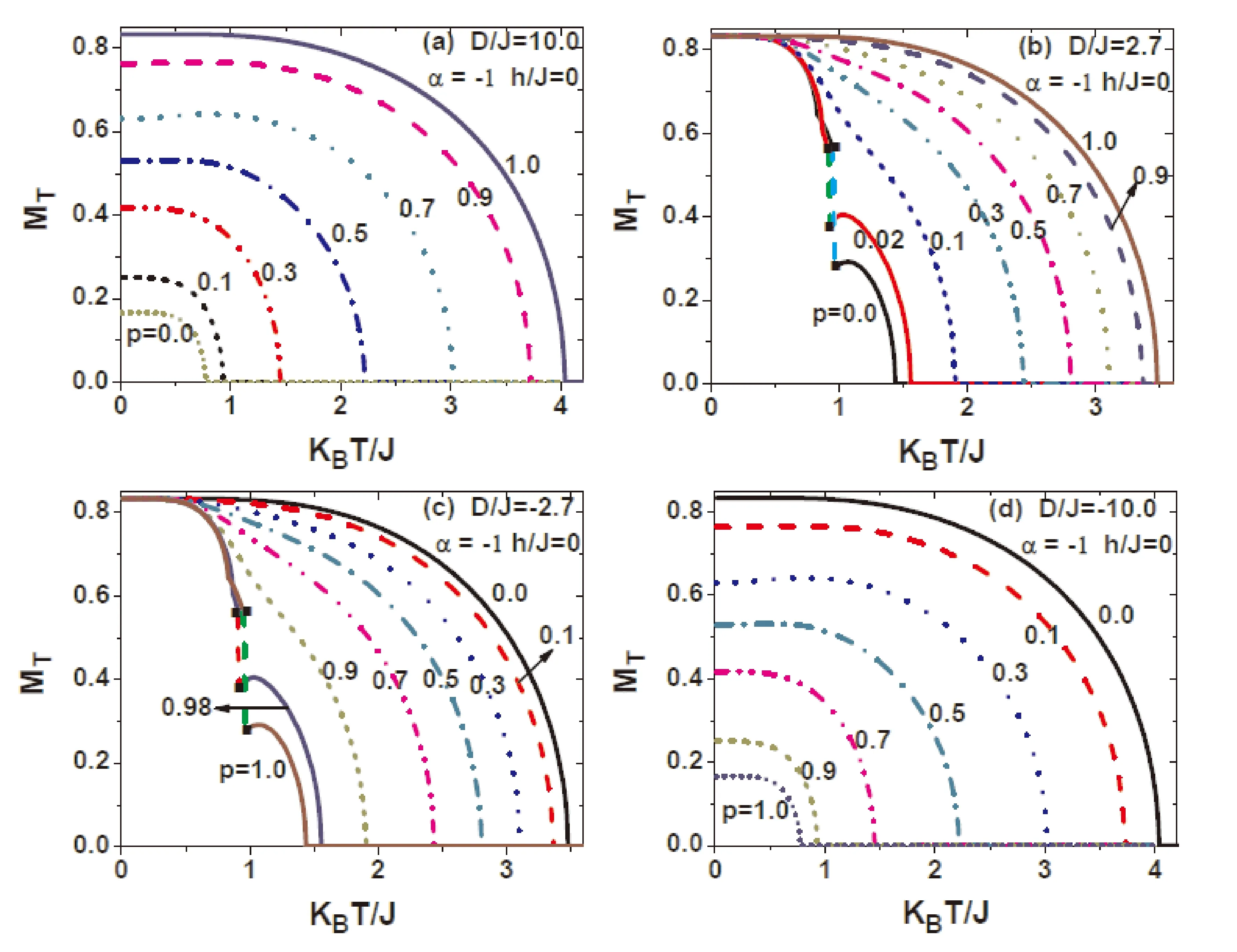
圖2 外磁場為0，晶場強度比值為-1，晶場參數D/J分別為(a) 10.0，(b) 2.7，(c) -2.7，(d) -10.0時，系統平均磁化強度隨溫度的變化曲線，曲線上的值為隨機晶場概率p.Fig.2 The temperature dependence of the magnetization is presented with some selected values of crystal field D/J (a) 10.0，(b) 2.7，(c) -2.7，(d) -10.0,when the external magnetic field is 0 and the value of D/J=-1.The real number on each curve denotes the value of p.

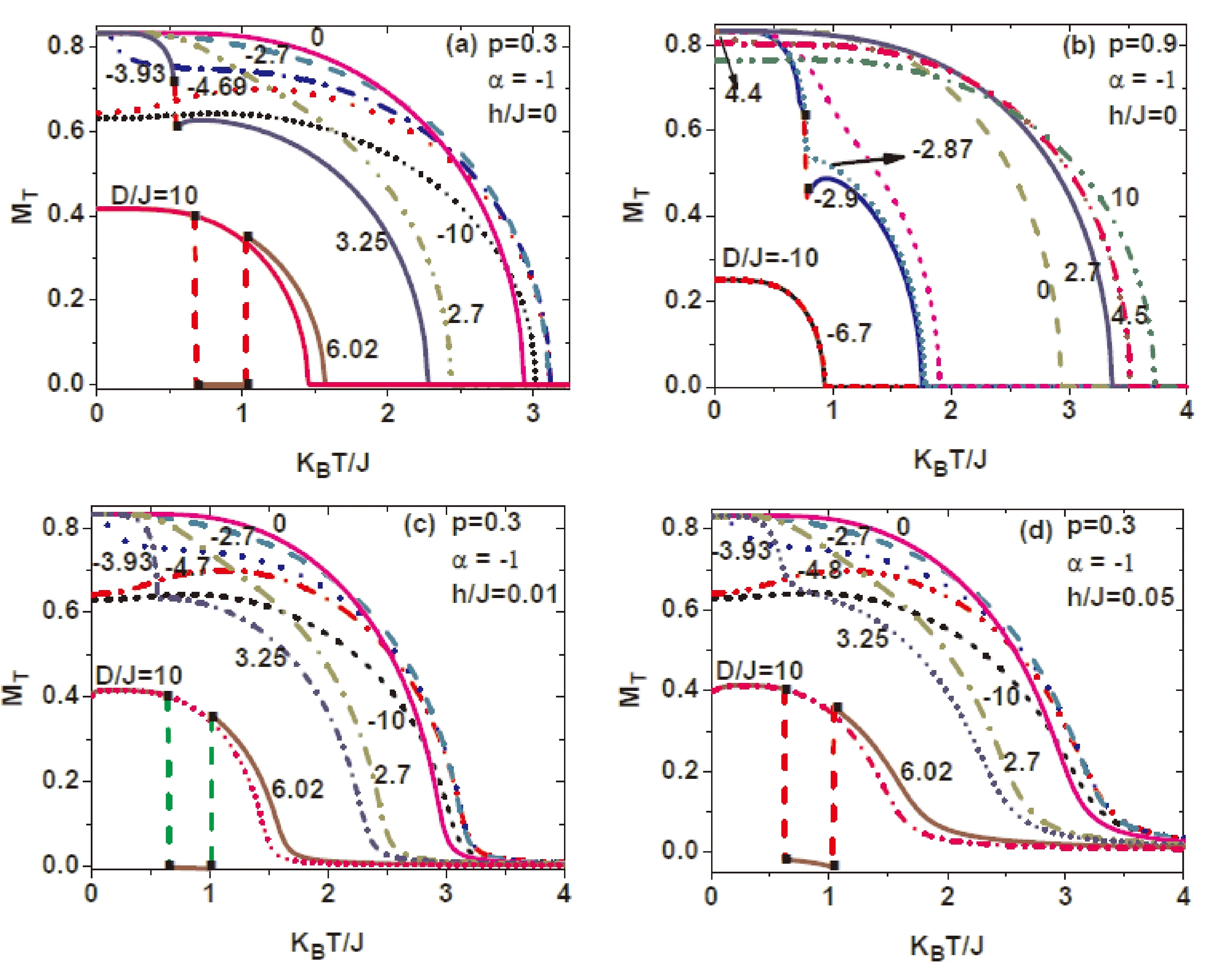
圖3 概率p=0.3和0.9時，系統平均磁化強度隨溫度的變化曲線，曲線上的值為晶場參數D/JFig.3 The temperature dependence of the magnetization is presented with some selected values of crystal field D/J,when the external magnetic field is not zero.The real number on each curve denotes the value of D/J

3.2 類對稱交錯晶場作用下，晶場參數和外磁場對系統平均磁化強度的影響

為了研究不同晶場強度下系統平均磁化強度隨溫度的變化情況，圖3(a)和(b)分別給出了p=0.3和0.9時，雙模隨機交錯晶場分布下平均磁化強度隨溫度的變化曲線.結果表明，p較小時，負晶場對磁化強度阻礙作用不明顯；晶場參數取正值時，系統發生一級相變；系統平均磁化強度出現缺失現象(平均磁化強度為零)；當D/J=-3.93且溫度較低時，磁化強度隨溫度的變化非常明顯，通過研究，我們認為是因為外殼層格點(藍色圓點代表的磁性原子)的配位數較小的原因.隨著p增大，負晶場對系統磁化強度抑制作用明顯，晶場參數取負值時，系統發生一級相變.雖然不同晶場強度作用下，系統平均磁化強度呈現出不同的磁化現象，但總體變化趨勢相似.為了研究外磁場對平均磁化強度缺失現象的影響，我們給出了圖3(c)和(d).從圖中可以看出，外磁場能夠減弱平均磁化強度缺失現象，但是缺失部分平均磁化強度呈現負值.

3.3 類非對稱交錯晶場作用下，外磁場為零時，概率對系統平均磁化強度的影響

圖4(a)—(f) 給出了晶場滿足類非對稱交錯晶場(例如α=-0.5)分布時，系統平均磁化強度隨溫度的變化曲線.圖4(a)和(b)及圖4(d)和(f)顯示，系統平均磁化強度隨溫度的變化曲線與圖2相似.但是當D/J=-5.8時，系統平均磁化強度隨溫度變化曲線局部出現負值(例如p=0.7,0.9,1.0)，見圖4(e)，說明原子摻雜程度(晶場強度比值α)不同，會使系統呈現出不同的磁化現象.

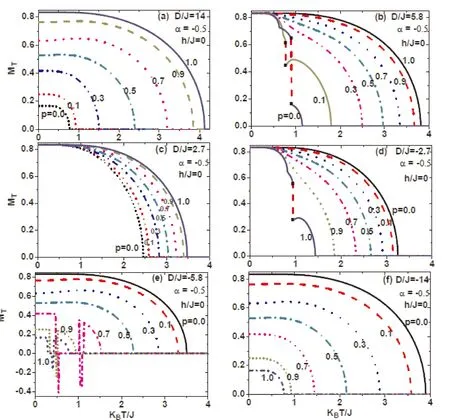
圖4 外磁場為0，晶場參數D/J分別為(a) 14，(b) 5.8，(c) 2.7，(d) -2.7，(e) -5.8，(f) -14時，系統平均磁化強度隨溫度的變化曲線，曲線上的值為隨機晶場概率p.Fig.4 The temperature dependence of the magnetization is presented with some selected values of D/J=14,5.8,2.7,-2.7,-5.8,-14,when the external magnetic field is 0.The real number on each curve denotes the value of p.

3.4 類非對稱交錯晶場作用下，晶場參數和外磁場對系統平均磁化強度的影響

為了研究不同晶場強度比值對系統平均磁化強度的影響，圖5給出了類非對稱交錯晶場作用下平均磁化強度隨溫度的變化曲線.結果顯示：概率較小和較大時，系統都存在一級相變和二級相變；外磁場較小時，沒有對系統平均磁化強度產生明顯的影響.但是系統平均磁化強度出現缺失和負值的現象更加明顯.我們認為導致這種現象的物理原理是不同原子摻雜，使得系統在一定條件下平均磁化強度出現負值.

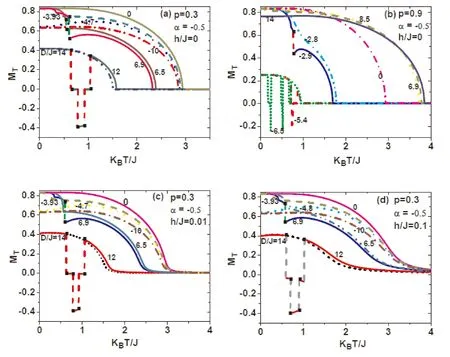
圖5 概率 p分別為0.3，0.9時，系統磁化強度隨溫度的變化曲線，曲線上的值為晶場參數D/JFig.5 The temperature dependence of the magnetization is presented with some selected values of the probability of p =0.3,0.9,when the external magnetic field is not zero.The real number on each curve denotes the value of D/J.

4 結 論

本文利用有效場理論研究了雙模隨機交錯晶場作用下spin-1和spin-1/2混合自旋BC模型系統的平均磁化強度隨溫度的變化情況.結果表明，系統格點的平均磁化強度與隨機交錯晶場的取值概率p、晶場強度比值α、晶場參數D/J、外磁場、溫度以及交換相互作用密切相關.概率P、外磁場、晶場強度比值和D等諸多因素相互競爭，使系統表現出比恒定晶場作用的BC模型更為豐富的磁化現象：系統格點的平均磁化強度隨溫度的變化曲線呈現缺失和負值的現象；P、α和D/J會影響系統的一級相變和二級相變.