基于正則化的函數連接神經網絡研究及其復雜化工過程建模應用

賀彥林，田業，顧祥柏，徐圓，朱群雄

（1 北京化工大學信息科學與技術學院，北京100029； 2 智能過程系統工程教育部研究中心，北京100029；3中石化煉化（集團）股份有限公司，北京100101）

引 言

近年來，隨著化工生產過程的日益復雜，生產過程數據也逐漸趨于高復雜、高非線性等特征，傳統的基于化工機理建模的方法已經無法處理當下復雜的化工系統。神經網絡技術作為一種新的數據驅動方法，其具有很強的非線性映射和學習能力，降低模型對機理的依賴，從數據的角度建立更加精確的模型，目前已經廣泛應用于各個領域[1-3]，其衍生出了多種神經網絡模型，如誤差反向傳播神經網絡[4]（BP），多層感知器模型[5]（MLP）等。然而，BP 網絡和MLP 網絡的層數和節點數選取缺少理論依據，導致網絡在計算復雜性和計算量上有一定難度，同時BP算法收斂速度緩慢。函數連接神經網絡（functional link neural network，FLNN）[6-8]作為一種新型神經網絡被Pao[9]提出，其網絡結構簡單，模型參數較少，具有非常好的非線性逼近能力。與傳統神經網絡結構作對比，函數連接神經網絡只有輸入層和輸出層，沒有隱藏層，因此函數連接神經網絡計算量更小，訓練速度更快，目前已經廣泛應用于建模[10-11]、預測[12-13]、分類[14-15]等領域。

然而，隨著工業系統規模的擴大，生產過程數據也越來越復雜，該網絡存在一些局限性，經過函數連接神經網絡擴展之后的數據維數和復雜度會更高，這大大提高了網絡的計算量，從而降低網絡的學習速度。同時由于FLNN 的權值求解方法采用的是梯度下降法，該方法的缺點是容易陷入局部極值，這會降低函數連接神經網絡的網絡精度。正則化是一種通過修正網絡權值，從而有效解決高計算量以及局部極值問題的方法。該方法根據其自身的數學理論基礎，充分利用輸入與輸出之間的關系，對輸出代價函數進行約束，使代價函數的解最優化，同時由于約束參數的影響，使其一定程度上能夠克服局部極值和過擬合問題[16-17]。函數連接神經網絡通過使用正則化方法計算得來的權值來進行學習，在網絡計算速度和精度上都有了提高。

由此，本文提出用正則化方法[18-21]來作為函數連接神經網絡（FLNN）的權值更新方法，減少原始網絡的計算量，提高模型精度和計算速度，改善了局部極值帶來的影響，最終建立一種基于正則化的函數連接神經網絡模型（regularization based functional link neural network,RFLNN）。為驗證該網絡模型的有效性，首先采用UCI 數據庫中的Real estate valuation 數據對其進行驗證；隨后將所提出的模型應用于HDPE生產過程建模。

1 函數連接神經網絡

函數連接神經網絡采用函數擴展的方式，對原始輸入進行擴展，使原始輸入轉化到另外一個空間，將增強后的模式作為網絡輸入層的輸入，通過這種方法來更好地處理非線性問題。該神經網絡由輸入層和輸出層構成，沒有隱含層，因此相較于傳統神經網絡，該網絡計算量更小，訓練速度更快。

1.1 FLNN結構及構造方法

FLNN結構圖如圖1所示。

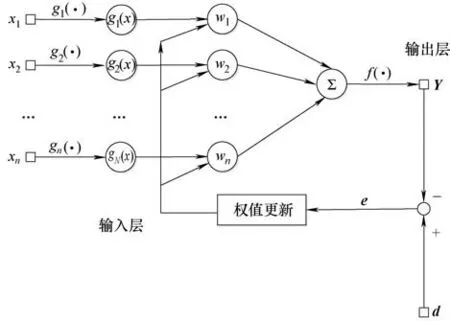
圖1 常規FLNN結構Fig.1 Structure of the FLNN model

建立FLNN模型的具體步驟為：

（1）設n維輸入向量：X =(x1,x2,…,xn)。

（2）對n維輸入向量進行函數擴展[22-23]，擴展函數可選擇如cos(πx)，sin(πx)，cos(2πx)，sin(2πx),…，設g(·)為擴展函數，經過擴展得到N維輸入向量g(x) =(g1(x),g2(x),…,gN(x))。

（3）設W 為神經網絡的權值向量：W =(w1,w2,…,wn)T，將擴展后的輸入向量與權值向量加權求和，得輸出層的輸入向量，即S =∑gw。S經過激活函數f(·)處理，則得到該神經網絡的輸出Y。

（4）將計算得出的網絡實際輸出Y 與期望輸出d 對比，求得誤差函數e(t)。通過誤差函數e(t)的變化來對權值向量W 進行調整，直到滿足神經網絡精度要求，或者學習次數終止為止。多次調整得來的權值即為FLNN的網絡模型參數。

1.2 傳統FLNN的局限性

常規FLNN 權值更新的方法一般是BP 算法[24-25]，將神經網絡的實際輸出量與期望輸出量差值的平方和最小化作為神經網絡的學習目標，數學公式為[26]

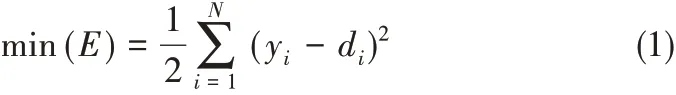
權值更新公式為

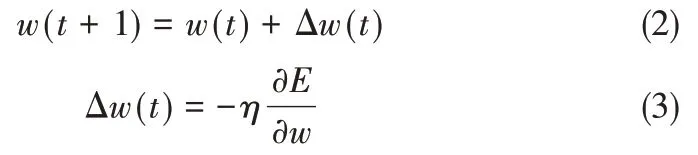
其中，η為學習率;t為固定時延。

將FLNN 網絡應用到化工過程建模中，不可避免會遇到一些問題。

（1）FLNN 自身權值更新采用的是BP 算法，而BP 算法通過使用梯度下降法來求解誤差函數E 的最小值，而這種方法的缺點[27-29]是容易陷入局部極值，同時BP 算法也容易出現過擬合的問題，因而會導致模型精度降低、收斂速度慢等問題。

（2）由于FLNN 采用的是先將原始數據進行增強擴展，而化工數據的高維度和高復雜化，會導致擴展之后的數據更加復雜，因而大大提高網絡計算量，降低網絡的計算速度和精度。

為了克服這些問題，本文結合正則化的方法，對FLNN 網絡的權值參數進行優化，通過使用正則化方法求得的權值，作為網絡的訓練最終結果，從而提高網絡的性能。

2 基于正則化方法的FLNN神經網絡

由于目前化工過程的日益復雜，過程數據也趨于高維化和復雜化，這導致常規的FLNN 在處理這些數據時，出現訓練速度偏慢、網絡精度低的問題。本文采用正則化的方法，對FLNN 進行權值參數的優化改進，不僅在計算速度上有了提升，而且網絡精度也有一定的提高。

2.1 正則化方法

正則化方法[30]其目的是通過將神經網絡代價函數最小問題的求解限制在一個壓縮子集中，利用正則化項平衡模型的網絡偏差，控制輸出的權值范圍，從而提高網絡的穩定性。其經驗公式為L=E+λF。其中，L 為正則化代價函數，E 為神經網絡損失函數，λ為正則化參數，F為正則化項。

下面對經驗公式各項進行具體的說明。

（1）損失函數 該函數用E 表示，設xi為訓練樣本；訓練輸出，即逼近函數為f(xi)；標準損失函數表達如下

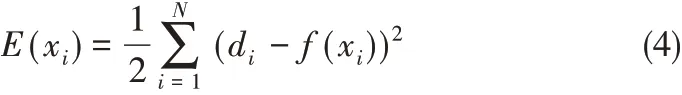
其中，di為訓練的期望輸出。

（2）正則化項 用F 表示，根據逼近函數，將正則化項定義為

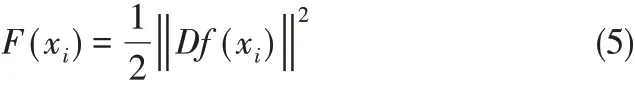
其中，D是線性微分算子，包含損失函數解的問題的先驗知識，因此D的選取與所解的問題有關，它使正則化問題的解穩定，使解滿足連續性要求。

（3）正則化代價函數 令正則化代價函數為L，結合式（4）中損失函數和式（5）中正則化項，L 最終表達為

其中,λ 是正則化參數，通常為正實數，用來控制正則化項F 和代價函數L 的最終解。當λ→0 時，則代價函數L 最小點問題的求解是無約束的，完全由樣本確定最終解；當λ→∞時，則表明樣本是不可靠的，代價函數L最小點問題的求解是不存在的；因此，通過訓練樣本和先驗知識，選擇一個合適的λ值，對求解L(xi)起很大的作用。本文選取的正則化參數λ=0.1。

正則化問題的解就是使代價函數L 最小化，根據微分的規則，對代價函數L(xi)進行Frechet 微分，有

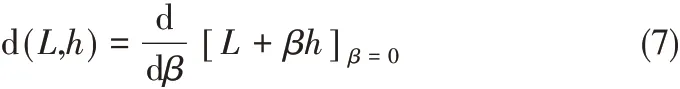
其中，h(x)是一個固定的關于向量x 的函數；為了簡化表示，用h來代替h(x)。

根據微分規則，對于h ∈x 集合，代價函數L(xi)有極值點的必要條件是

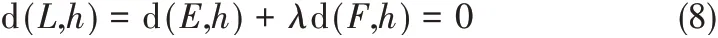
其中，d(E,h)與d(F,h)分別是損失函數E(x)和正則化項函數F(x)的Frechet微分。

代價函數L(x)的Frechet微分結果如下

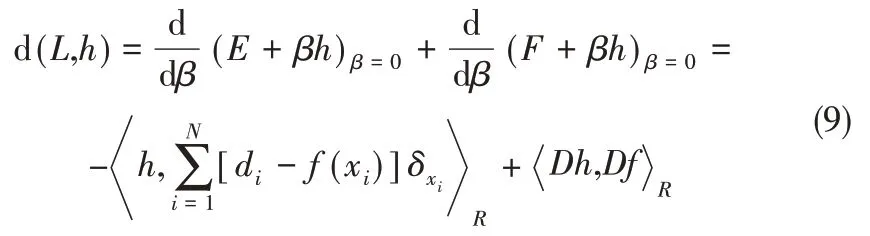
根據Green恒等式，可以將式（9）改寫為

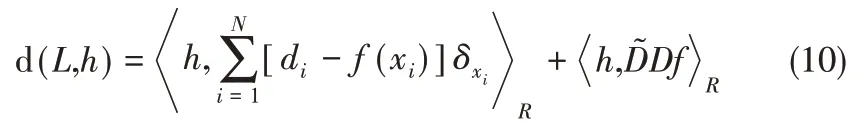
最終計算得

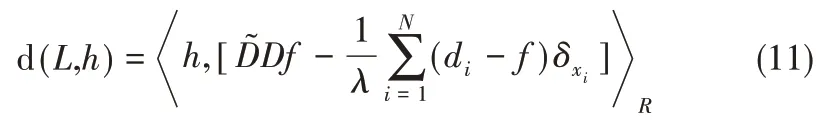
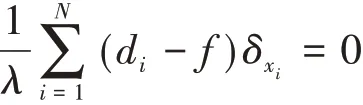
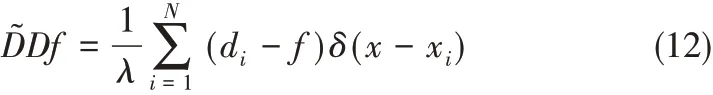
由Green函數的連續性可知

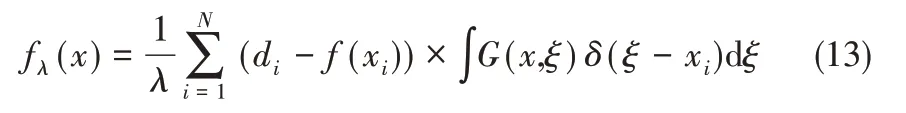
其中，fλ(x)為代價函數L(x)的最小解在經過N個Green 函數的線性疊加；G(x,ξ)是關于x 的Green函數，ξ為定值。

對式（13）化簡可得

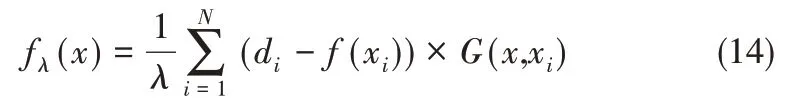
令權值

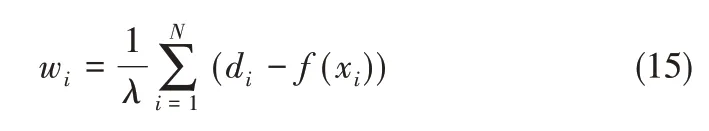
則

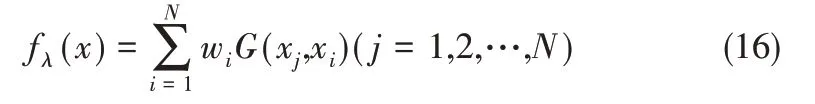
將式（15）、式（16）寫成矩陣形式

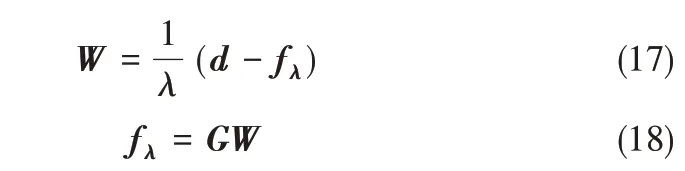
其中，fλ、d、G、W 分別為fλ(x)、di、G(xj,xi)、wi的矩陣表達。

式(17)、式(18)相消可得

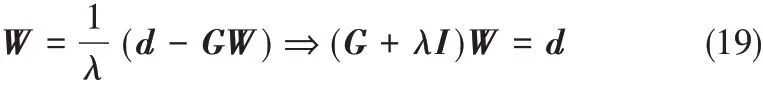
其中，I為N × N的單位矩陣。

當矩陣(G + λI)是正定矩陣時，權值W 可表示為

由于式(20)求解權值的解局限于權值W、Green函數G、期望輸出d 是相同維數的，因此為了得到通用解W，引入N × N的對稱陣G0，使得

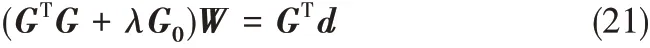
得權值的最終解為

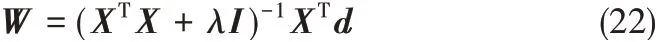
2.2 基于正則化的FLNN

本文提出基于正則化的函數連接神經網絡，網絡結構圖如圖2所示。

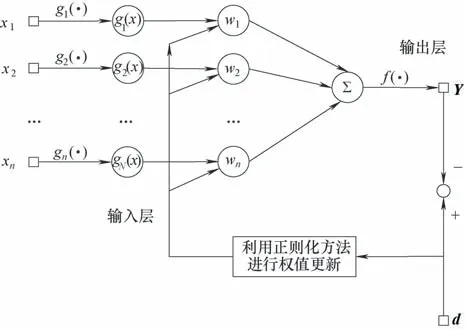
圖2 RFLNN網絡結構Fig.2 Structure of R-FLNN model

給定網絡訓練樣本集合S，S 中包含K 組高維數據S ={(Xk,Yk)|k = 1,2,…,K; Xk∈RL; Yk∈RJ}，其中每個訓練樣本的輸入含有L個屬性，輸出含有J個屬性。對于訓練樣本S，建立RFLNN模型如下。

（1）數據預處理：由于數據中各個變量的量綱不一定相同，使得數據與數據之間沒有可比性，因此需要對給定的輸入樣本數據進行歸一化處理，本文設定的歸一化范圍為（0.1,0.9），歸一化函數為

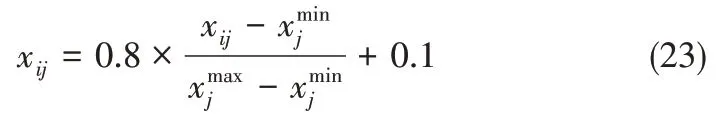
（2）函數擴展：選擇擴展函數對歸一化后的數據進行函數擴展，增強數據的非線性，本文選用的擴展函數有正弦函數g1(·)、余弦函數g2(·)、Sigmoid函數g3(·)。通過擴展，提高輸入數據的維度，擴展后的數據變為N維網絡輸入變量

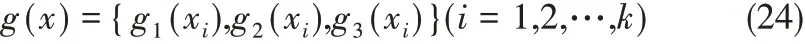
數據集變化為S'={(Xn,Yk)|Xn∈RI; Yk∈RJ;n = 1,2,…,N; k =1,2,…,K}，其中RI是經過函數擴展之后的新輸入樣本集合，RJ保持不變。

（3）建立RFLNN 模型，以擴展后的數據Xn作為輸入層的輸入，通過正則化方法求解出輸入層與輸出層之間的連接權值

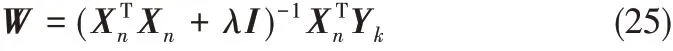
其中，Yk為FLNN 網絡的期望輸出，Yk∈RJ，n =1,2,…,N; k = 1,2,…,K。

（4）訓練：對RFLNN模型進行訓練，將訓練得出的最終數據yi進行反歸一化，并計算實際輸出與期望輸出的相對誤差。反歸一化公式為

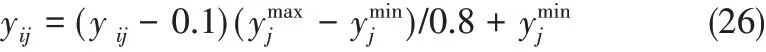
（5）泛化：利用泛化樣本的數據對訓練好的RFLNN 網絡進行驗證，計算網絡泛化的期望輸出和實際輸出之間的相對誤差。算法流程圖如圖3所示。

3 實驗結果分析

利用UCI 數據庫中的Real estate valuation 數據集以及化工行業HDPE 的生產數據對所提出的RFLNN模型進行驗證，并與傳統FLNN對比。

3.1 標準數據實驗分析

為初步驗證此方法的可行性和有效性，本文采用UCI 數據庫中的Real estate valuation 數據集對所提出的RFLNN 模型進行測試，Real estate valuation數據是一個對房地產估價的數據集，有6 個輸入屬性和1 個輸出屬性，共414 組數據，隨機分為訓練數據（總數據的三分之二）和泛化數據（總數據的三分之一）。

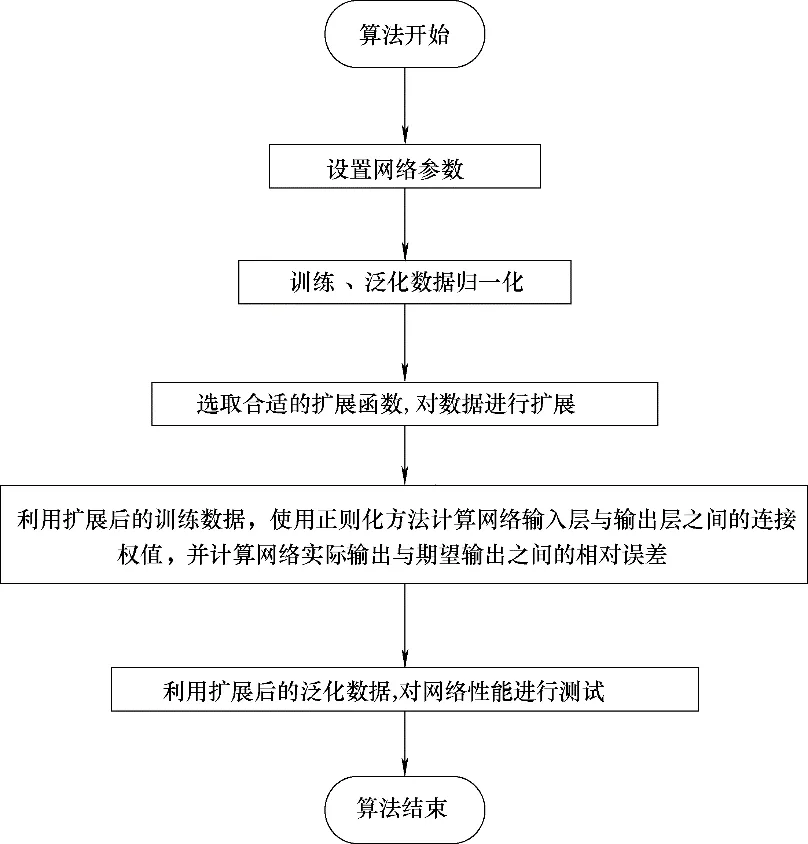
圖3 RFLNN網絡算法流程Fig.3 Flowchart of R-FLNN algorithm

設置網絡的輸入層和輸出層節點數為6和1，傳統FLNN 網絡的學習因子設為0.1，迭代次數為1000次。將數據分別作為RFLNN 和傳統FLNN 的輸入，得到網絡訓練的殘差分布，如圖4所示。

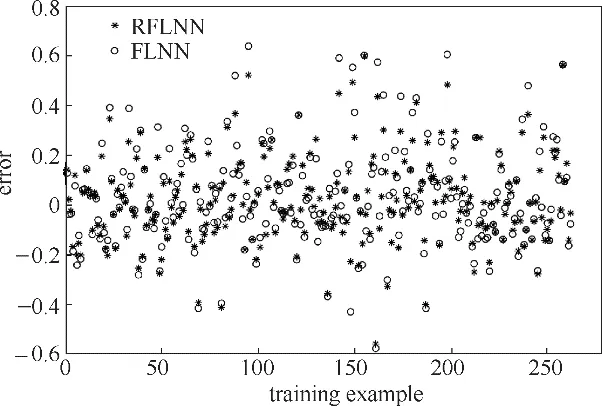
圖4 網絡訓練過程的殘差分布Fig.4 Residual error distribution of real estate valuation data training examples with two models

從圖4 可以看出，網絡訓練得出的輸出與真實值相近，可以說明網絡有效性和可行性。

對網絡的實際輸出與真實值進行對比，計算出訓練階段和泛化階段的平均相對誤差，比對結果如表1所示。由表1 的對比結果可以看出，RFLNN 相對傳統FLNN 訓練和泛化平均相對誤差都有降低，說明RFLNN 網絡泛化能力更強，精度更高，在局部極值和過擬合問題方面處理地較好。

表1 UCI數據集模型建模時間和精度對比Table 1 Performance comparisons of models for estate valuation data

3.2 HDPE工業應用數據實驗分析

3.2.1 HDPE 簡介 高密度聚乙烯（high density polyethylene，HDPE），是一種結晶度高、非極性的熱塑性樹脂，主要用于生產薄膜、管材等塑料產品。生產高密度聚乙烯采用的是德國Basell 的Hostalen低壓淤漿工藝進行懸浮聚合，該裝置主要以乙烯為原料，1-丁烯為共聚單體，用氫氣調節分子量，通過將乙烯、1-丁烯、氫氣、催化劑等連續加入聚合反應器內，控制好聚合物的質量，從而生產高密度的聚乙烯。因此，為了生產高密度的聚乙烯，控制好聚合物的質量，對國內外相關企業在減小損失和生產成本方面起積極作用。

依據工業機理和經驗知識，確定輸入變量為15、輸出變量為1的樣本數據集，其中樣本數據集的輸入變量是主要影響聚合物質量的15個因素，輸出變量為密度指數。通過對現場采集數據，并對數據進行融合、濾波、去干擾等預處理后，共采取135 組生產數據，隨機選取90組數據（總數據的三分之二）作為訓練數據，其余45組數據（總數據的三分之一）作為泛化數據，傳統FLNN 學習因子為0.1，迭代次數為1000次，傳統FLNN 和RFLNN 輸入層和輸出層節點數分別為15和1。

3.2.2 訓練結果對比 圖5為網絡訓練的輸出和真實值對比圖，圖6是網絡訓練的殘差分布。

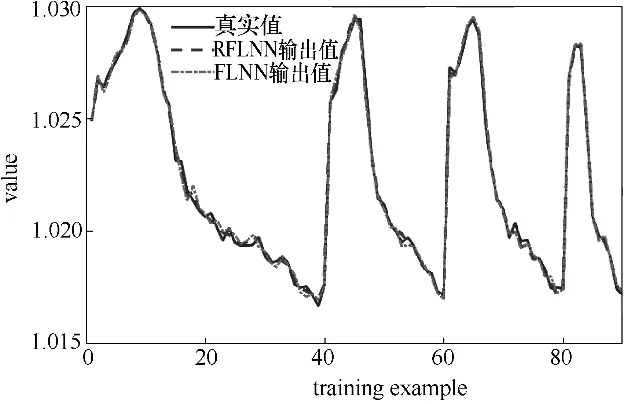
圖5 網絡訓練的輸出和真實值的對比Fig.5 Comparisons of training examples with two models

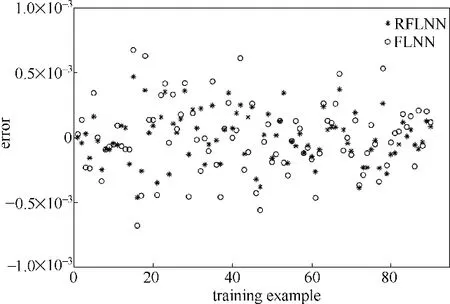
圖6 網絡訓練的殘差分布Fig.6 Residual error distribution of training examples with two models

從網絡訓練輸出與真實值的對比圖及殘差分布圖可以看出，RFLNN 網絡訓練輸出更加接近真實值，RFLNN網絡訓練的平均相對誤差是0.0156%，而傳統FLNN網絡訓練的平均相對誤差是0.0214%，相對誤差較小，說明訓練過程中RFLNN網絡模型更精確。從訓練時間角度可以看出，RFLNN 網絡訓練時間為0.0024 s，傳統FLNN 網絡訓練時間為0.3918 s，訓練時間明顯縮短，說明RFLNN 網絡計算量降低，收斂速度更快。

3.2.3 泛化結果對比 圖7為網絡泛化的輸出和真實值對比圖，圖8為網絡泛化的殘差分布圖。

RFLNN 網絡的泛化平均相對誤差是0.0365%，而FLNN網絡泛化的平均相對誤差是0.0505%，由此說明RFLNN網絡泛化精度更高。

FLNN 和RFLNN 網絡應用于HDPE 過程建模在訓練和泛化所花時間，以及平均相對誤差比對結果如表2所示。

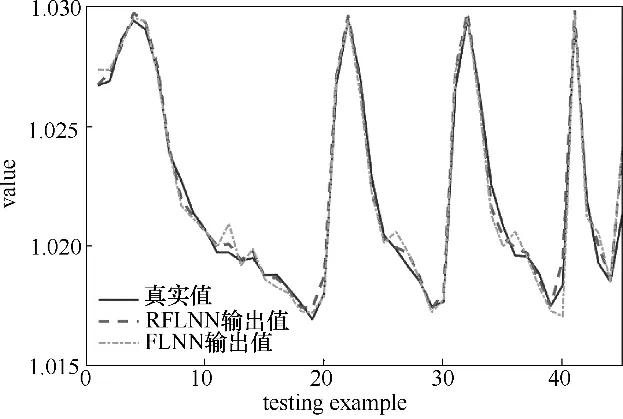
圖7 網絡泛化的輸出與真實值的對比圖Fig.7 Comparisons of testing examples with two models

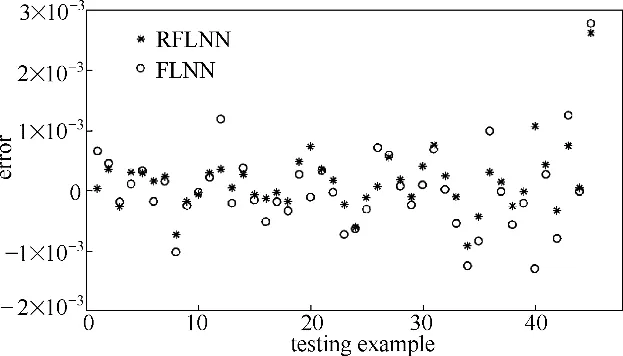
圖8 網絡泛化的殘差分布Fig.8 Residual error distribution of testing examples with two models

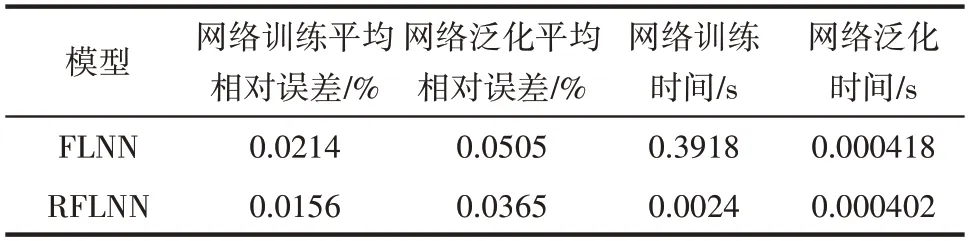
表2 工業建模應用時間和精度對比Table 2 Comparisons of model performance for HDPE samples

通過表2 可以看出，RFLNN 網絡訓練和泛化的平均相對誤差都有所降低，說明了本文提出的RFLNN 網絡模型精度更高，泛化能力更強，且在保證模型精度的情況下，RFLNN網絡收斂速度更快。

4 結 論

針對復雜的化工過程建模問題，本文提出了一種基于正則化的函數連接神經網絡模型，此模型是在傳統的FLNN 網絡模型的基礎上，通過對權值更新的算法進行優化，利用正則化方法計算權值的優越性，從而改善網絡處理數據的性能，提高網絡的學習速度和精度。為了驗證所提模型的有效性，本文選取UCI 標準數據Real estate valuation 以及HDPE 生產過程數據進行仿真實驗。仿真結果表明，本文所提出的基于正則化的FLNN 模型相比于傳統的FLNN 模型，具有收斂速度快、模型精度高、泛化能力強的優點，且能夠有效避免局部極值和過擬合的問題，為復雜石化過程建模提供新思路。