培養高階思維 促進深度學習
——例談數學運算課高階思維培養策略

夏建華

（威海市第二實驗小學，山東 威海 264500）

數學運算是指在明晰運算對象的基礎上，依據運算法則解決數學問題的過程。主要包括：理解運算對象，掌握運算法則，探究運算方向，選擇運算方法、設計運算程序，求得運算結果等。在數學運算核心素養的形成過程中，教師應引領學生進一步發展數學運算能力，能有效借助運算方法解決實際問題；能夠通過運算促進數學思維發展，養成程序化思考問題的習慣；形成一絲不茍、嚴謹求實的科學精神。

傳統的課堂教學，不注重引領學生充分經歷知識的形成過程，簡單將算法告之學生，再加以練習鞏固，這種教學行為帶來的學習效果往往是學生只從表面上掌握了計算技能，但為什么要這樣算，卻說不清道不明，把算理教學教成了低階思維的記憶層次，不利于學生高階思維的發展。怎樣讓學生自主探究算理、歸納算法，樂于運算也學有價值，是我對本節課的目標追求與實踐思考。

一、類比遷移，整體架構，培養思維的深刻性

思維的深刻性，是指思維活動的抽象程度和邏輯水平，以及思維活動的廣度、深度和難度。它既表現在嚴密的思維活動過程之中，又表現在思維活動結果的廣度和深度之上，并能經受實踐的檢驗，達到舉一反三、觸類旁通的效果。

在溫故環節中，我重點引領學生復習兩方面的知識（如圖）：一是復習三年級時學過的積的變化規律。通過兩組口算，尋找因數和積的變化規律，為后面學習小數乘小數時需觀察兩個因數的變化引起積的變化做好鋪墊；二是復習上節課學過的小數乘整數。通過筆算說算理“你是怎么算的？為什么這樣算？”讓學生知其所以然，為后面學習小數乘小數時尋找最近的生長點，將小數乘整數的方法遷移到小數乘小數中。

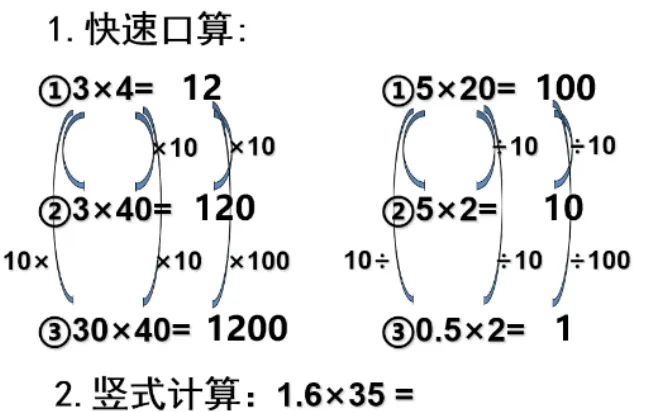
在新授環節，我以學生感興趣的購物場景進行導學：橙子13.9元/kg，西紅柿7.88元/kg，小蘭買0.9千克的橙子和1.5千克的西紅柿各花了多少錢？在解決兩個問題中，學生分別列出算式13.9×0.9和7.88×1.5，并觀察這兩道乘法算式與之前學過的乘法算式有什么區別？學生通過回顧、對比，發現這兩道算式都是小數乘小數，而之前學過的是整數乘整數、小數乘整數，這是本課中學生第一次認識“小數乘小數”。而后，學生憑借自己的經驗，自主嘗試進行小數乘小數的兩道豎式計算。在交流、辨析中，發現小數乘小數與小數乘整數的計算既有共性，也有不同。共性之處在于它們都是把小數乘法轉化為整數乘法算出乘積后，再根據因數和積的變化規律確定積中的小數點的位置。不同之處在于：一是小數乘小數不像小數乘整數只關注一個因數的變化，而要同時關注兩個因數的變化；二是小數乘小數不像小數乘整數乘積比它本身大，而有可能會出現乘積比它本身還小的情況。在對比中，引導學生合理進行遷移，同時凸顯小數乘小數的本質特征，這是本課中學生第二次認識“小數乘小數”。接著我又呈現了一組直接說結果的計算練習（如圖），讓學生在短時間內根據相應的整數積，快速說出“小數乘小數的積”，學生認識水平越來越高，最后一組拋開具體的數只有抽象的符號表達式，學生也能慧眼識別，探究的氛圍迅速升到了最高點，整個課堂的學習氣氛達到了熾熱化。此時，學生對小數乘小數的理解真可謂“撥開云霧見月明”，這是本課中學生第三次認識“小數乘小數”。

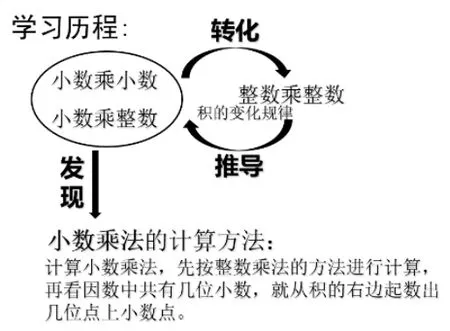
總結環節中，先請學生自主歸納小數乘小數的計算方法，并引領學生思考這種方法是否適合于之前學過的小數乘整數，接著拋出問題：“現在你會算三位小數乘兩位小數、四位小數乘三位小數嗎？……”一連串的問題，讓學生反思、感悟到只要是小數乘法，其實算法都是通用的，以此從整體上幫助學生架構了一個完整的小數乘法知識體系（如圖），同時學生思維的深度和廣度也得到了發展。

二、循理入法，以理馭法，培養思維的批判性

思維的批判性，是指能夠對問題、論述、證據等進行辯證性的思考，從而提出或形成自己的觀點。批判性思維是一種審視真偽、理性推論的思維方式，不僅包含“獨立思考”，還包含“真理多元”，如憑證據講話、合乎邏輯地論證觀點、善于提出不同問題、不懈質疑、對自身的反省和對異見的包容。

在《小數乘小數》一課中，算法與算理孰重孰輕？其實，算法、算理是運算能力的一體兩翼，兩者相輔相成，不可偏廢。道理很簡單，不掌握算法就無法確保實現運算能力的最低要求“正確”；只知怎樣算，不知為什么這樣算，充其量只是搬弄數字的操作技工。新授課中，我將重點放在如何讓學生理解算理上，只要能理解算理，再跟進必要的練習鞏固，算法的掌握便是水到渠成的事。

首先，在復習小數乘整數時，讓學生進行豎式筆算1.6×35 ，并說出自己是如何算的。在說出算理之后，針對小數末尾有0的特殊情況適時評價：為什么一位小數乘整數，原則上乘積是一位小數，而這里卻寫了整數？

接著，在探究小數乘小數時，解決第一個問題：買0.9千克的橙子花了多少錢？學生自主嘗試豎式筆算，并交流自己的算法。交流中，有學生質疑：為什么這道乘法運算，積變小了？還有學生問：為什么一位小數乘一位小數，積卻是兩位小數？解決第二個問題：買1.5千克的西紅柿花了多少錢？學生自主嘗試豎式筆算，請學生代表交流自己是怎么算的。交流中，有學生問：為什么7.88與1.5在豎式計算時沒有將小數點對齊？還有的學生問：為什么兩位小數乘一位小數，積卻是三位小數？在給出“整數積”后直接說出“小數積”時，學生自主發現小數乘小數的規律：因數中一共有幾位小數，積就有幾位小數。有學生追問：為什么因數中一共有幾位小數，積就有幾位小數？這些核心問題的拋出，讓學生在思辨中越辯越清，理越說越明。

由此看來，學生的思維狀態決定著學生數學學習的整體效能，發展學生高階思維是數學教學的應有之義。在數學運算教學中,教師可以通過創設學生學習的合理情境、建構學生學習的心理場境、打造學生學習的實踐場域,引領學生深度體驗、深度認知、深度實踐,讓深度學習真實發生！培養學生的高階思維，是我們課堂教學中應努力追尋的方向！