生長及耗散波色-愛因斯坦凝聚中的怪波

張志強，何章明

(1.鄭州商學院通識教育中心，鞏義 451200；2.湖南工業大學理學院，株洲 412007)

1 引 言

怪波(Rogue wave)[1]最初是描述海洋上出現的一種奇怪的水波，它以其出現的突然性和異常陡峭的高水波得名.怪波是一種特殊的非線性波，具有來無影去無蹤，且破壞力大的特點[2,3].與孤子類似，怪波也是一種新的非線性現象，都是非線性偏微分方程的一種特殊解[4-7]，不同的是怪波的產生機制源于調制不穩定性，目前在非線性光學[8]、等離子體物理[9]、流體物理[10]和波色-愛因斯坦凝聚(BEC)[3,11-16]等領域中觀察到怪波現象.怪波理論是一種新的理論，無論在理論上還是具體工程應用上，都需要大力發展相關研究工作.

理論上，BEC的動力學行為可以用平均場近似下的Gross-Pitaevskii (GP)方程描述[13,15,17,18].對于生長及耗散的情況，波色-愛因斯坦凝聚與周圍熱原子團之間存在粒子交換，這時可以在GP方程中引入一個虛數項[19]，表示生長及耗散對BEC系統的影響.

對于描述一般的非線性系統的非線性薛定諤方程，尋找其精確解是困難的工作[5,6].常用的求解非線性偏微分方程的方法有：反散射法、行波變換法[20]，多重尺度方法[21,22]、達布變換法[10,23,24]等等.達布變換法是求解非線性薛定諤方程的一個有效方法，為研究非線性系統提供了一個非常重要的手段.

當前，對怪波的研究主要集中在研究一般形式的薛定諤方程中的怪波解[5-7,11]，而研究BEC中的怪波，主要探討將在BEC囚禁在不同的勢阱中，如含時和不含時的諧振勢阱[12]、光晶格勢阱[3]、PT對稱勢阱[15]等，研究這些變化的勢阱對怪波的影響，此外還有研究BEC中原子間相互作用[14]對怪波性質的影響.開放BEC系統受到外界的影響，BEC處于生長或耗散狀態之中，對于開放BEC系統中怪波的性質，我們目前研究的還不夠深入.本文，利用達布變換法，解析的研究了生長及耗散BEC中的怪波，根據解析結果，數值模擬了生長及耗散BEC中怪波的性質，并對結果進行討論.

2 生長及耗散BEC的怪波解

2.1 理論模型

基于平均場理論，生長及耗散的超冷原子BEC可用下面修正的Gross-Pitaevskii (GP)方程來描述

(1)

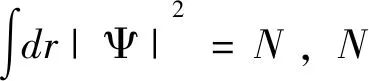
(2)

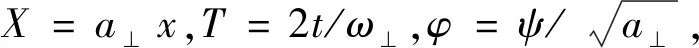
(3)

其中，g=2Nas/a⊥，γ=2Γ/(?ω⊥) .本文中考慮as<0，即BEC中原子間為相互吸引作用，同時考慮BEC形成以后關閉諧振勢阱，即諧振勢阱的橫向囚禁頻率ωi=0.

2.2 達布變換及怪波解

接下來使用Darboux變換法來求解方程(3).構造如下的Lax對，

Φx=UΦ=λJΦ+PΦ,

(4a)

(4b)

為求解Lax對(4)，我們選取方程(3)的一個初始解

(5)

其中Ac為實常數.將(4)式代入一次Darboux變換關系式

(6)

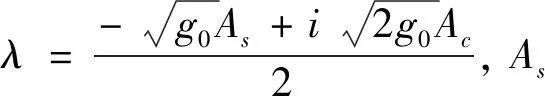
(7)

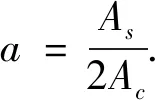
3 結果與討論

根據當前的實驗結果，我們選取5000個7Li原子形成的BEC凝聚體，軸向囚禁頻率ω⊥=2π×100 Hz，則無量綱化后的單位長度和單位時間對應的實際長度和實際時間分別是3.8 μm和3.2 ms.

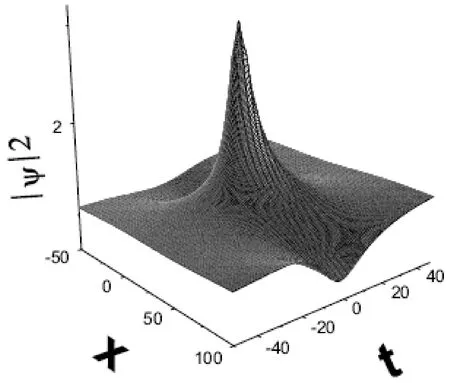
圖1 BEC中的雙洞怪波Fig.1 The rogue wave with two holes in BEC

為了對比，首先考慮BEC沒有生長或者耗散的情況，即選取γ=0，其他參數選取Ac=0.8，As=1.5，g0=0.1，然后根據(7)式畫出了圖1.如圖1所示，在BEC沒有生長或耗散時，BEC中的原子在t≈-30開始積聚，并在時間t=0時刻，一個非常高的峰出現在x≈0.而在高峰的兩邊，凝聚體的BEC背景密度比其他時刻的要小.隨著時間的推移到t≈30，高峰很快地消失，背景密度也恢復到平均值，因此這是一個典型的雙洞怪波.

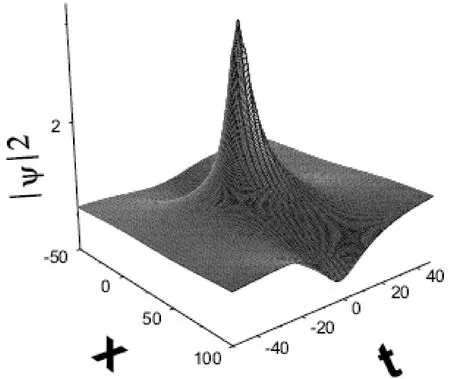
圖2 生長BEC中的雙洞怪波Fig.2 The rogue wave with two holes in a growth BEC

接下為了研究生長BEC中的怪波性質，選取γ=0.001，其他參數選取與圖1一致，根據(7)式畫出了圖2.在生長BEC中，如圖2所示，仍然會出現一個雙洞怪波.隨著時間推移，BEC一直從外部熱原子云中吸收原子，所以BEC的背景密度一直在緩慢增加.與BEC沒有生長或者耗散的情況做對比，隨著時間的推移到t≈40，怪波消失.這說明BEC的生長可延緩怪波消失的時間.

最后，為了研究耗散對BEC中怪波的影響，選取γ=-0.001，其他參數選取與圖1一致，然后根據(7)式畫出了圖3.在BEC的耗散過程中，如圖3所示，BEC中仍然出現的是一個雙洞怪波.隨著時間推移，BEC因為耗散而不斷丟失原子，所以BEC的背景密度一直在減小.隨著時間的推移到t≈20，怪波消失.這說明BEC的耗散加速了怪波的消失.

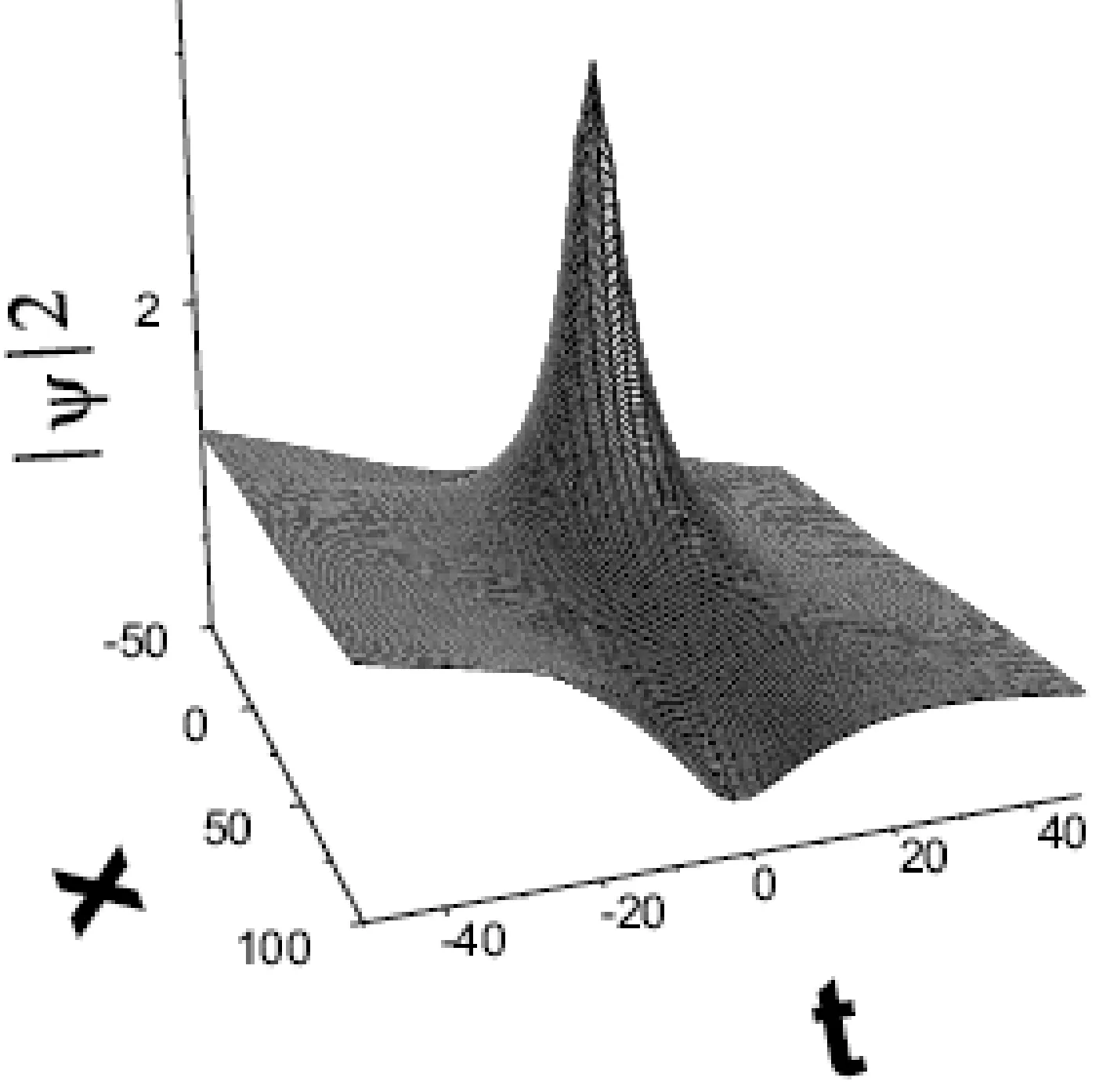
圖3 耗散BEC中的雙洞怪波Fig.3 The rogue wave with two holes in a dissipation BEC

4 總 結

總之，考慮BEC生長或者耗散情況，從三維GP方程出發，首先通過降維和無量綱化處理，得到一維非線性薛定諤方程.然后選取BEC中原子間相互作用為吸引相互作用，利用Darboux變換法求解了非線性薛定諤方程，得到了生長和耗散BEC中的怪波解.最后根據得到的解析解，數值模擬了BEC中怪波的性質.結果表明，BEC中出現的一種典型的雙洞怪波，并且BEC生長會延緩怪波的消失，而BEC的耗散會加速怪波的消失.