MoP在高壓下的電子，聲子和電聲耦合性質的第一性原理計算

葛 雨

(1.合肥物質研究院強磁場中心,合肥 230031;2.中國科學技術大學,合肥 230026)

1 引 言

拓撲材料是近幾年凝聚態物理領域的研究熱點之一[1].2011年，南京大學萬賢綱等人通過理論計算第一次提出，燒綠石結構銥氧化物可能是磁性Weyl半金屬[2].同一年，徐剛等人理論預言鐵磁尖晶石HgCr2Se4也是Weyl半金屬[3].物理所翁紅明等人預言了一系列中心反演對稱性破缺的弱關聯材料是Weyl半金屬，并被實驗所一一驗證[4].2017年，翁紅明等人又成功預言了三重簡并費米子的存在[5]，并迅速被物理所錢天等在MoP的角分辨光電子能譜(ARPES)實驗測量中所證實[6].壓力是重要的物理學參量，壓力直接影響晶體結構從而能夠極大地改變物質的物理性質，在高壓下可以發現很多新的常壓下難以觀測的物理學現象[7-12].2015年，H2S在極高壓下達到了203.5 K的超導轉變溫度，刷新了新的超導轉變溫度記錄[13],引發了研究人員對高壓超導體的關注[14-17].2018年研究人員發現MoP在30 GPa左右發生超導轉變，臨界轉變溫度TC為2.5 K左右，隨著壓力增大，TC也隨之升高，在95 GPa時升高到4 K.另外，在60 GPa以下，MoP的晶體結構非常穩定，表明受晶體結構對稱性保護的拓撲非平庸電子態和超導態在高壓下共存，這使得MoP成為研究拓撲超導現象的很好的平臺[18].

拓撲材料MoP在高壓下的超導相變引發了很多關注，但其內部的超導轉變機理尚沒有確切的解釋.對材料本身的直接實驗研究主要集中在電輸運和電子結構，其晶格動力學性質隨壓力的變化的實驗研究存在一定的困難.因此，希望使用理論計算的方法研究MoP的聲子性質和電聲耦合性質.基于密度泛函理論的第一性原理方法可以精確簡便的模擬體系在高壓下的狀態，近年來有很多的成果，成為了我們的首選[19-22].總的來講，本文使用基于密度泛函理論的第一性原理計算，得到了MoP在不同壓力下的電子結構，聲子結構，電聲子耦合參數.根據麥克米蘭(McMillan)經驗方程擬合了MoP在不同壓力下的超導轉變溫度，與實驗結果一致，從理論計算的角度證明了MoP在高壓下的超導轉變是由于電聲子耦合作用加劇，符合BCS理論模型框架.

2 計算細節

MoP在0到50 GPa的晶體結構由晶體結構搜索軟件USPEX(Universal Structure Predictor:Evolutionary Xtallography)搜索得到[23]，之后使用了基于密度泛函理論的VASP(Vienna ab initio simulation package)[24]軟件包，使用投影綴加平面波方法(PAW)[25]進行結構優化和電子能帶的計算.載斷能選取為335 eV，k點網格為18×18×18.晶體動力學和電聲子耦合計算使用的是基于密度泛函微擾理論[26]的QE(Quantum ESPRESSO)軟件包[27]，截斷能選取的是200 Ry，贗勢選取為Troullier-Martin型的模守恒勢[28]，交換關聯泛函(GGA-PBE)被使用[29]，k采樣為18×18×18，q點采樣為9×9×9.

3 理論背景

超導是低溫下重要的物理現象，目前比較好解釋常溫超導現象的理論是BCS理論[30,31].基于BCS理論和已有的實驗數據，WL.McMillan得出了一個計算超導轉變溫度半經驗公式，也就是麥克米蘭方程(1)[32].這為常規超導體超導轉變溫度的理論計算提供了可能.

(1)

在這里，Θ是德拜溫度，它與超導轉變溫度TC成正比，與原子質量成反比，μ*是有效的庫倫作用勢，一般μ*的數值選取0.1-0.13最為合適，本文中μ*取0.1.λ是電聲子耦合參數，它直接反映電聲子耦合的強弱，盡管λ并不正比于超導轉變溫度TC，但是大量的研究表明數值較大的λ有利于獲取高的TC.

當λ小于1時候，麥克米蘭可以簡化成公式(2)[33]，由此我們得知TC主要和ωlog和λ有關.

(2)

ωlog是聲子振動頻率的對數平均值，由聲子能量直接計算得到，表示為:

(3)

(4)

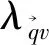
(5)

將公式(4)代入公式(5)中可得公式(6):

(6)

也可以表示為譜函數的積分的形式(7):

(7)

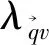
4 結果與討論

4.1 MoP晶體結構

使用USPEX代碼，結合進化算法和第一性原理總能量計算我們獲得了MoP在高壓下的晶體結構.圖1(b)顯示了MoP的晶體結構，屬于空間群P -6 m 2(編號187).在晶格中，M原子的Wyckoff占位為1a(0,0,0)，P原子的Wyckoff占位為1d(1/3,2/3,1/2) .晶體結構對稱操作包括旋轉對稱性C 3 z和鏡像對稱性M y和M z，這對拓撲保護三重簡并點是至關重要的.經過結構優化，不同壓力下MoP晶格常數的演變如表1所示.總的來講，隨著壓力增大，晶格常數減少.

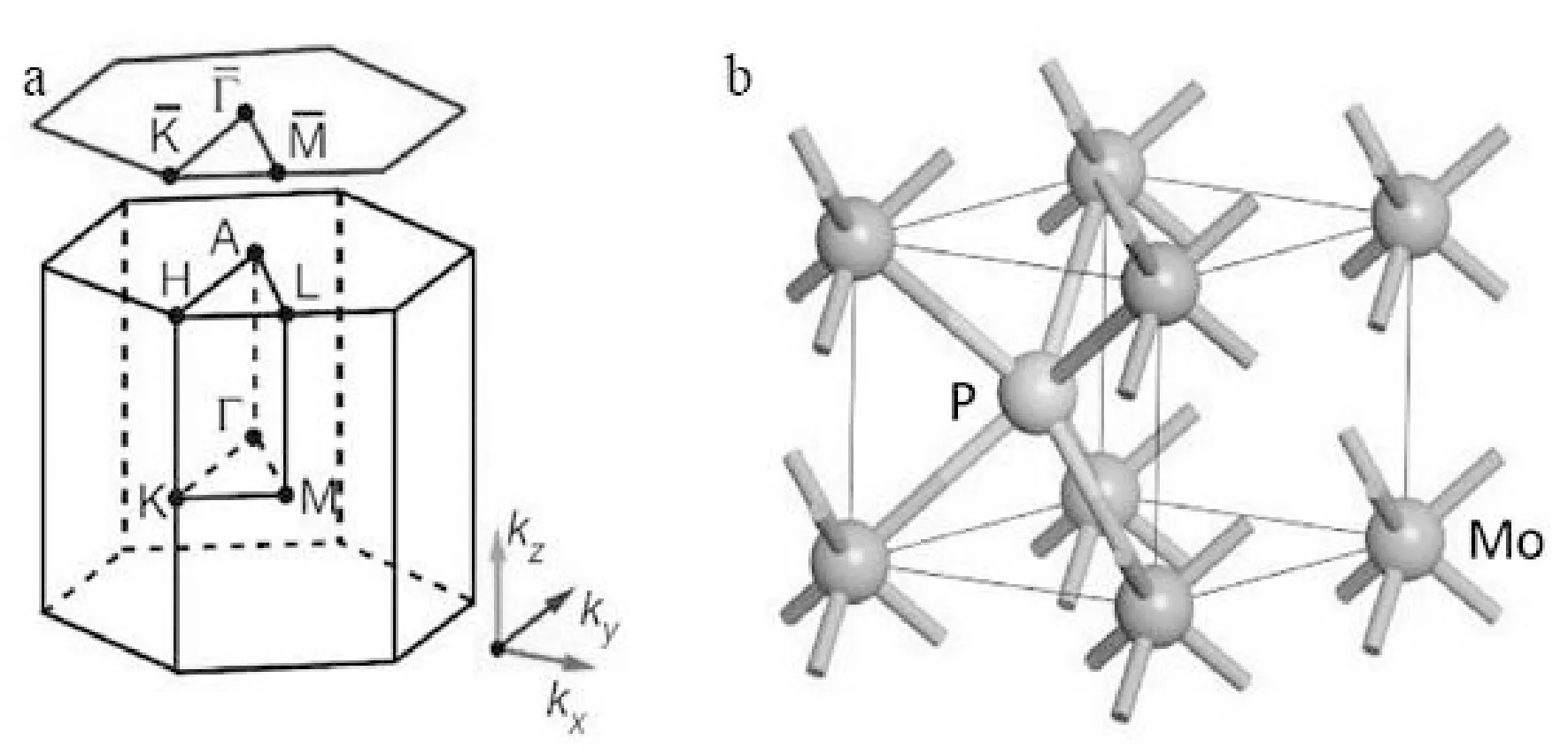
圖1 (a)MoP布里淵區高對稱點,(b)MoP的晶體結構示意圖Fig.1 (a) High symmetry point in Brillouin zone of MoP,(b) Schematic diagram of the crystal structure of MoP

表1 MoP在不同壓力下的晶格常數Table 1 Refined lattice constants of MoP at various pressures.

4.2 MoP不同壓力下的電子結構

如圖2所示，a-f分別是MoP在0 GPa，30 GPa，50 GPa下，考慮自旋軌道耦合(Spin-orbit coupling ,SOC)(左)和沒有考慮自旋軌道耦合(右)的能帶圖，布里淵區高對稱點為Γ-K-M-Γ-A-H-L-A(圖1(a)).從圖中我們可以得出，MoP呈現金屬性.盡管壓力發生很大變化，但費米面附近的電子結構變化很小，費米能級發生輕微變化，這是由于壓力下MoP沒有發生結構相變導致的.為了探究不同原子和軌道對于電子結構的貢獻，我們繪制了0 GPa下的電子態密圖(圖3).從圖中可以看出，費米面附近主要是Mo的d軌道和P的p軌道.

總的來說，壓力沒有對電子結構產生大的影響，MoP在高壓下仍保持了受晶體結構對稱性保護的拓撲非平庸電子態，與已知的理論計算結果是一致的[34]，這為研究物質拓撲相與超導電性之間的相互作用提供了一個極好的平臺.

4.3 MoP不同壓力下的聲子能譜與態密度

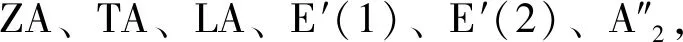
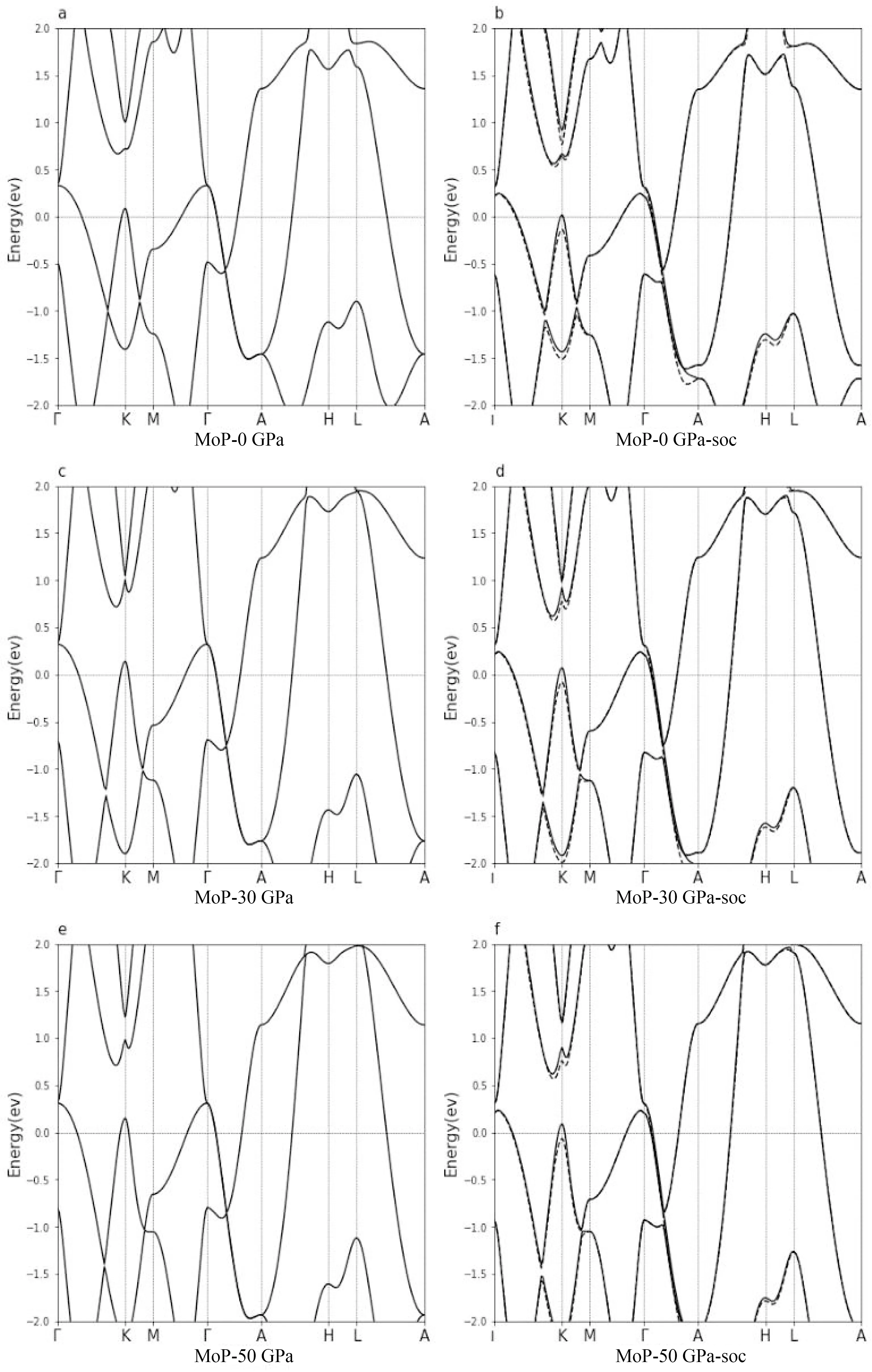
圖2 MoP在0 GPa (a,b),30 GPa (c,d),50 GPa (e,f)下，不考慮(左)和考慮(右)自旋軌道耦合的能帶圖.Fig.2 The electronic band structure of MoP at 0 GPa (a,b),30 GPa (c,d),50 GPa (e,f) without SOC(left) and with SOC(right).

4.4 MoP隨壓力變化的超導轉變溫度

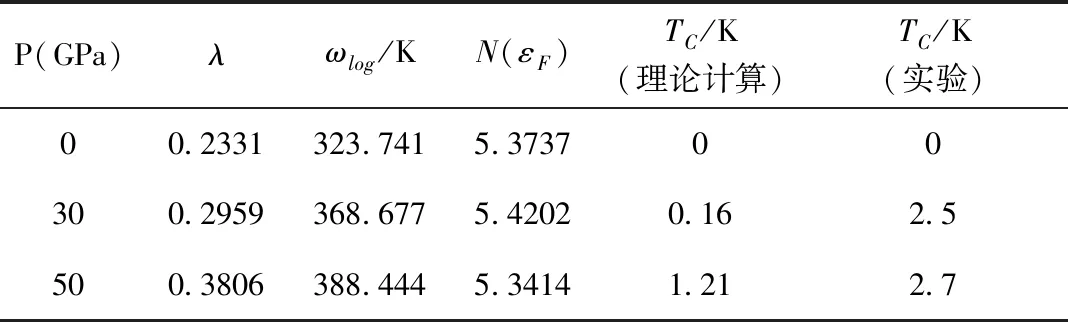
最后，我們計算了0 GPa到50 GPa下的ωlog和λ值，帶入公式(2)計算得到TC的值，并與實驗的TC進行比較.由表3可知，隨著壓力的提高，費米能級處的電子態密度N(εF)變化極小，這與電子結構隨壓力變化極小是一致的.而聲子振動頻率的對數平均值ωlog和電聲子耦合參數λ值均隨著壓力的升高而增大，體系的電聲子耦合隨壓強的增大而逐步變強，導致超導轉變溫度從常壓下的零提高到30 GPa時的0.16 K，最后在50 GPa時提高到1.21 K，與實驗的變化趨勢基本一致.

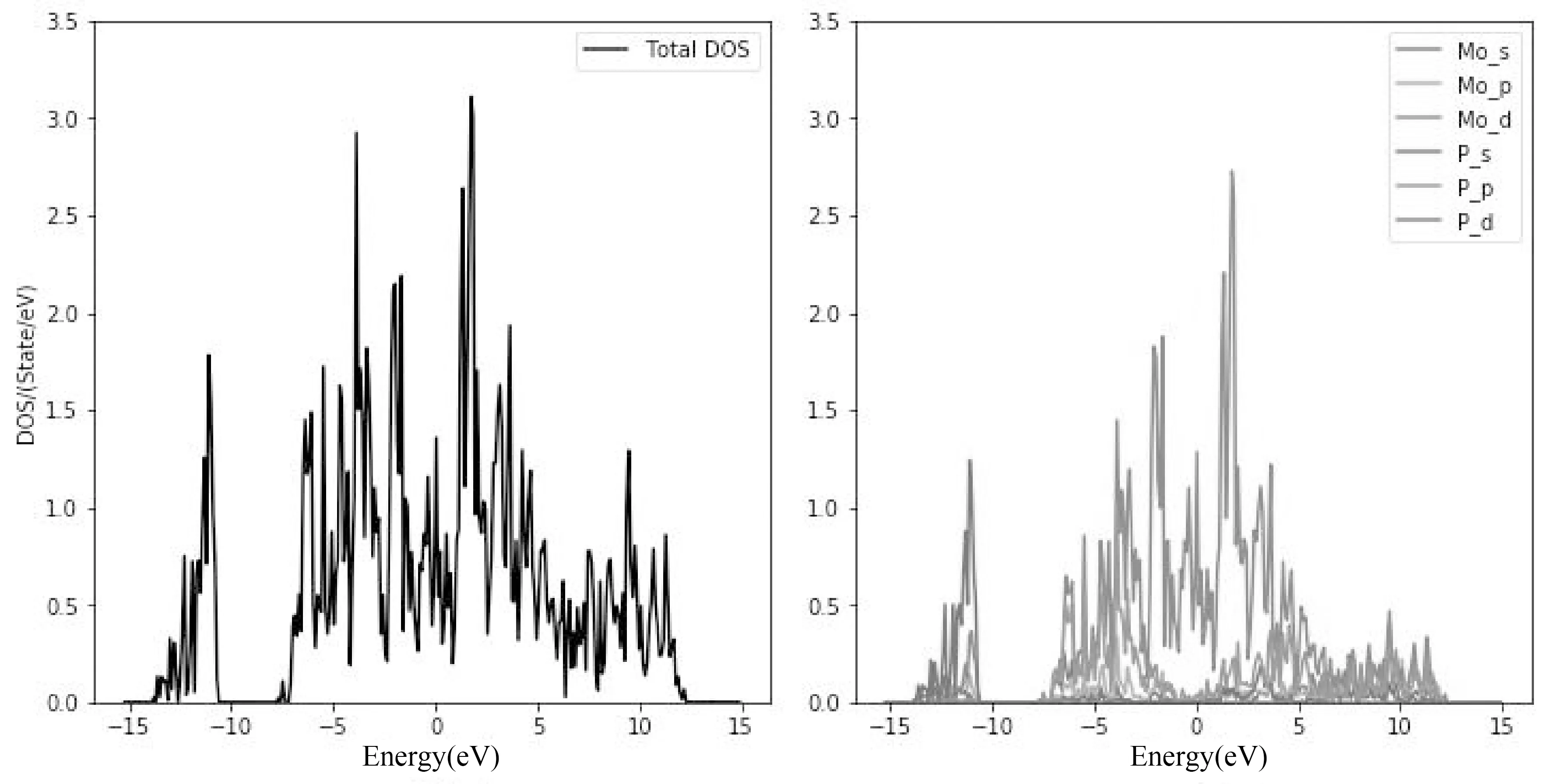
圖3 MoP在0 GPa的電子態密度圖.Fig.3 The density of states (DOS) for MoP at 0 GPa

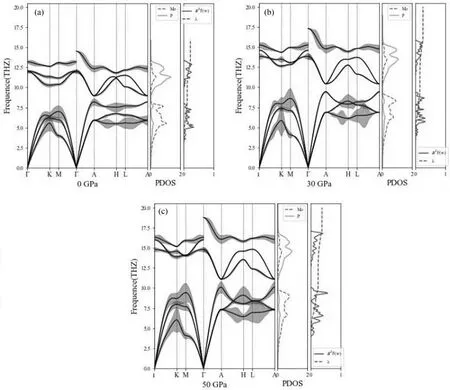
圖4 MoP在0 GPa (a),30 GPa (b),50 GPa (c)下的聲子色散圖，聲子態密度圖，譜函數圖和積分電聲子耦合參數圖.聲子色散圖線周圍的陰影的厚度表示了每個q點處的聲子線寬強度與頻率的比值.Fig.4 Phonon chromatic dispersion spectrum,phonon state density spectrum,spectral function graph and integral electron-phonon coupling parameter map of MoP at 0 GPa(a),30 GPa(b) and 50 GPa(c).The thickness of the shade around the phonon dispersion line represents ratio of the intensity of the phonon line width to frequency at every q point.

表2 MoP各個聲子振動模式對電聲子耦合參數的貢獻
Table 2 Contribution of different phonon vibration modes of MoP to electron-phonon coupling parameter (The first three are acoustic branches and the last three are optical branches)

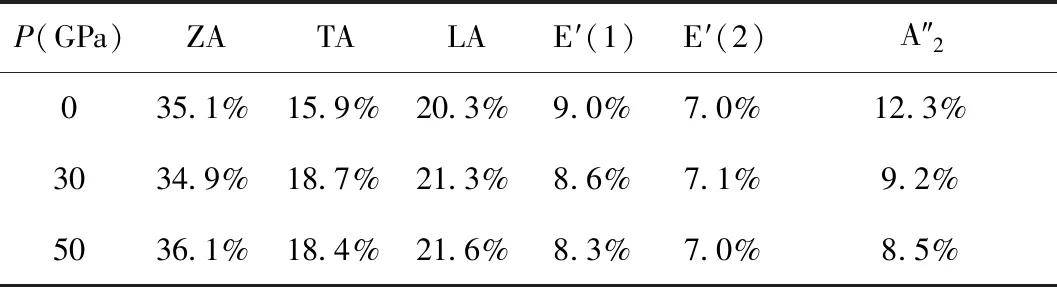
P(GPa)ZATALAE′(1)E′(2)A″2035.1%15.9%20.3%9.0%7.0%12.3%3034.9%18.7%21.3%8.6%7.1%9.2%5036.1%18.4%21.6%8.3%7.0%8.5%

表3 理論計算得到的隨壓力變化的電聲子耦合參數λ、聲子振動頻率的對數平均值ωlog和費米能級處的電子態密度N(εF)，以及理論計算和實驗得到的超導轉變溫度TC.
Table 3 Electroacoustic coupling parameterλ,logarithmic mean of phonon vibration frequency ωlogand electronic state density at Fermi levelN(εF) through theoretical calculation,and theoretical and experimental values for superconducting transition temperature.

P(GPa)λωlog/KN(εF)TC/K(理論計算)TC/K(實驗)00.2331323.7415.373700300.2959368.6775.42020.162.5500.3806388.4445.34141.212.7

綜上，我們的理論計算可知，MoP在高壓下的超導轉變是符合BCS理論框架的.其中電子結構變化較小，不是超導轉變的主要原因.而聲子結構隨著壓力升高發生光學支整體上升硬化，聲學支部分下降軟化的現象.聲子結構的變化使得ωlog和λ均隨著壓力升高而增大，兩者共同作用導致超導轉變溫度的升高.

5 結 論

我們使用第一性原理計算方法探索了MoP在高壓下的晶體結構，電子結構，晶格動力學以及超導電性.研究表明，隨著壓力的增大，MoP的晶格常數減小，電子結構幾乎保持不變.而聲子能譜光學支部分呈現整體上升硬化，聲學支存在部分下降軟化，這是電聲子耦合參數增加的主要原因.計算得出，聲子振動頻率的對數平均值ωlog和電聲子耦合參數λ值均隨著壓力的升高而增大，導致超導轉變溫度從常壓下的零提高到30 GPa時的0.16 K，最后在50 GPa時提高到1.21 K，與實驗超導轉變定性上一致，說明MoP在高壓下的超導轉變是符合BCS理論框架的,為理解實驗觀測到的拓撲超導共存現象提供了一定的理論支持.