中職數學應用思維導圖 提升學生數學思維能力

孫妮妮

（濰坊市工業學校，山東 濰坊 261300）

引言

在中職數學教學中，為了更好培養學生的數學思維能力，最為首要的任務便是讓教師積極轉變自身傳統教學方式。在傳統教學方式下，大都是教師在黑板上寫和在講臺上講，這樣使得學生學習地位十分被動，學習積極主動性難以被很好的調動，數學思維培養自然無從提及。再加上數學知識比較抽象化，所以學生學習理解起來也存在較大的難度。而合理應用思維導圖，則能很好解決這些問題，加深學生對相關知識點的認識與理解。就這一方面而言，加強中職數學應用思維導圖，提升學生數學思維能力的分析探究意義重大，具體如下。

一、中職數學教學中學生思維培養現狀

在當前的中職數學教學過程中，學生的數學思維能力往往不被重視，教師的重點大都放在學生應試能力的培養上，從而使得學生數學思維能力水平很不理想，具體表現為：一是很多學生反映數學學習難度大；二是課堂上學生很少主動發言；在作業完成過程中，學生存在抄襲、逃避等行為。即便有會做的題，但是稍微變化一下就不知道從何下手了；三是在考試過程中，學生審題不清，難以從題目中提取有價值的信息，思維系統性很差。

常規中職數學教學中，教師往往側重于知識的教授，盲目應用灌輸式教學模式，忽視了學生課堂主體性的體現，使得學生學習起來十分被動，學習積極性明顯不足，思維活動較弱[1]。這樣導致學生對于知識的理解往往比較淺顯，從而不能靈活應用，對于學生未來發展極為不利。

二、思維導圖在中職數學教學中的應用措施

（一）通過思維導圖呈現知識點

在傳統教學模式下，中職數學教師的教學通常會借助板書形式，不過所應用的板書基本都是綱要式的，簡單羅列知識點，然后讓學生做筆記，在課后進行背誦。這種方法雖然能夠起到一定的效果，不過對于學生發散思維能力的培養卻極為不利。而合理應用思維導圖，則能加深知識點間的聯系，促使學生思維發散。具體需要教師先歸納相同類型的知識點，深入分析知識點間的聯系，為“圖狀結構”的應用做好鋪墊[2]。在這一過程中，需要中職數學教師充分考慮到學生的個體差異性，雖然很多優秀的學生可以在一個知識點學習的同時銜接到其他相關的知識點，并自主進行匯總，不過對于一些數學基礎薄弱的學生來說是很難做到這一點的。

例如在集合這部分知識學習過程中，很多中職學生對于集合之間的關系缺乏深刻的認識與理解。為此，教師在具體教學中，便可以結合課程知識與學生實際合理繪制思維導入（見下圖1），以便讓學生更好理解與掌握集合知識與集合知識間的關系，而且還能靈活應用。

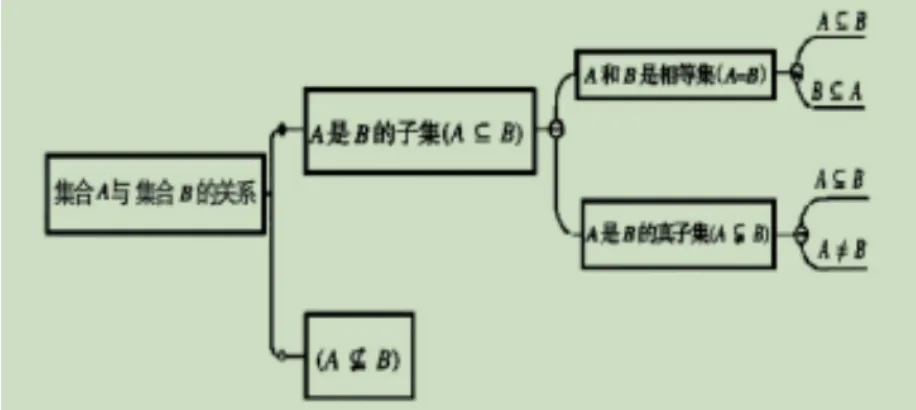
圖1

（二）借助思維導圖，鍛煉學生數學思維

思維導圖是一種創新性的思維工具，其與傳統思維方式最大的區別在對解決問題時，要求思維者跳出固定思維，對問題進行獨立思考和分析，并借助已有的知識經驗來分析和解決問題。而學生在利用思維導圖進行問題思考和解決時，需要提前制定目標，并結合自身已有的數學知識對問題進行思考和分析，最終找到問題解決的最佳方式。如此一來，對于學生數學思維的提升能夠起到很大的幫助。

在中職數學中幾何問題的證明過程是最能夠體現思維活動的。在對這類問題進行思考和解決的過程中，教師就可以引導學生利用思維導圖，在自己已有知識水平的基礎上，將抽象、復雜的幾何問題轉變為具體、簡單的問題，以便學生更好的對問題進行分析，從而提升學生的解題能力。例如，在對“圖形的相似”這一部分的幾何問題進行思考時，教師就可以引導學生利用思維導圖，將這一問題與之間所學的三角形知識相結合，通過這二者知識點之間的層次關系，將圖形相似問題轉變為證明三角形全等問題，以此來簡化數學問題，提升學生數學思維能力。

（三）通過思維導圖開展數學復習教學

任何一門的學科知識學習都得注重復習，中職數學學科也不例外。在具體課堂教學中，雖然解題技巧與思路對于學生的學習很重要，不過幫助學生搭建完善的知識結構也不容忽視，有助于加深學生的記憶。在傳統復習模式下，教師往往一個模塊一個模塊的教授，教師復習的吃力，學生學習起來也很為難。而且復習完成之后，學生對于數學知識點的認識依舊很模糊，甚至還有可能搞混淆。為了更好強化學生的數學思維能力，中職數學教師可以在復習環節合理應用思維導圖，這樣不僅能簡化知識，而且還能節省大量的復習時間。

例如在函數知識學完之后，在復習環節，教師便可以引導學生自己動手繪制相應的函數思維導圖，這樣便能進一步加深學生對函數各個知識點間聯系的認識，從而更加牢固的掌握。通過這種方式，能夠很好鍛煉中職學生的作圖能力，提升他們的數學思維能力，而且對于學生未來的學習發展也有著很大的促進作用，現實意義重大。

三、結語

綜上所述，在中職數學教學中合理應用思維導圖，能夠很好激發學生的數學思維，加深學生對數學知識的認識與理解。在思維導圖實際制作中，可以將各個數學知識點間的層次性關系很好展示出來，這樣學生在學習過程中，便能一目了然，而且在相關數學問題解答過程中，也會有著更為清晰的思路。所以可以說，思維導圖的應用對于學生數學思維能力的發展有著很大的促進作用，需要中職數學教師加強重視。