單線激光雷達與GNSS/INS的空間重構

王 銳，常 鍇，符國浩，王世峰，徐熙平*，王作斌

(1.長春理工大學 光電工程學院，吉林 長春 130022；2.長春理工大學 電子信息工程學院，吉林 長春 130022；3.長春理工大學 國家納米操縱與制造國際聯合研究中心，吉林 長春 130022)

1 引 言

隨著無人駕駛車輛[1]、機器視覺[2]的快速發展，三維空間重構技術[3]在諸多領域都發揮著不可或缺的作用。該技術廣泛應用于文物保護、建筑設計、道路檢測識別等場景，同時在游戲開發、臨床醫學等研究上也起到輔助作用[4]。三維空間重構技術通過數據獲取、預處理、點云配準和融合、生成空間表面等過程，把真實場景描述成符合計算機邏輯表達的數學模型。目前，國內外已經究出多種三維重構的方法：基于雙目立體視覺成像[5]，它屬于被動三維測量，該方法匹配計算代價較高，并且計算無紋理表面深度信息的準確度差；結構光測量[6]，結構光測量技術通過投影結構光可控地增加被測物體的紋理信息，測量精度高，但是投影儀標定與校正非線性誤差的過程較為復雜；應用較多的方法是利用CCD攝像機[7]獲取致密的圖像灰度信息和激光雷達提供的深度信息得到空間三維重構結果，但在兩種不同類型的數字信息的配準過程中易引入較大誤差，標定精度受限；利用多線激光雷達[8]進行三維空間的重構是目前應用最為廣泛的方法之一，但該方法的主要缺陷是采集數據量過大，點云數據配準的實時性有延時，對運算處理器配置要求較高以及價格較昂貴等。

本文提出了一種結合單線激光雷達和慣性導航模塊GNSS/INS系統來進行空間三維重構的研究。利用單線激光雷達反饋的數據確定二維平面數據點的距離角度信息，并結合GNSS/INS測量航向角的大小，確定掃描點經過的空間三維數字信息，將在不同幀獲取的數據分別融合、配準，最終得到該傳感系統的絕對空間掃描結果。該方法在顯著提高運算效率的同時保證了點云配準的精度。

圖1 UTM-30LX雷達的工作掃描區域Fig.1 Working scanning area of UTM-30LX lidar

2 系統設計

單線激光雷達利用飛行時間法(Time of Flight，TOF)[9]實現距離的測量，并且結合測角技術直接獲取目標點的角度信息。實驗中選用的激光雷達傳感器是由日本HOKUYO公司生產的UTM-30LX單線激光雷達。該款激光雷達擁有30 m的有效測量距離、270°水平測量角度以及25 ms的掃描時間，能夠較為精確地獲取短距離、廣角度的平面深度數據，并以此進行實驗仿真。圖1是Hokuyo激光雷達的工作參數示意圖。為了更加便捷地實現本文所提出的三維空間重構方法，本文將人為地給單線激光雷達提供不同的航向角來增加掃描維度，將不同幀的二維面融合配準得到重構的三維空間。同時選用GNSS/INS組合導航系統來確定實驗中任意提供的不同方向的航向角。該組合導航系統集成了三個MEMS陀螺儀和三個MEMS加速度計，GNSS衛星導航系統等。系統在靜態、動態和沖擊振動狀態下均有很好的響應，可以精確地獲取傳感器的姿態和加速度信息。UTM-30LX和GNSS/INS的詳細參數如表1所示。

表1UTM-30LX和GNSS/INS的工作參數

Tab.1 Working parameters of UTM-30LX and GNSS/INS

性能參數UTM-30LXGNSS/INS工作電壓12VDC±10%4.2～17 V頻率40 Hz800 Hz(max)工作溫度-10 to 50 ℃-40 to 85 ℃測量精度0.1 mm±0.5°

3 空間三維重建過程

當傳感器獲得空間掃描信息數據時，依據其反饋數據的上位機的Linux時間戳，兩傳感器的初始采集數據起始時間一致，并結合在MATLAB實驗平臺上的插值函數找出在時間戳上匹配的激光雷達掃描距離數據信息和GNSS/INS的航向角以及對應的三個方向的加速度信息，利用四元數[10-11]算法整合在各個不同位置(采集數據點)的掃描點云信息，生成不同幀的圖像。分別對GNSS/INS三個方向的角加速度值施以頻域積分，實現點云空間位置的粗配準，近似得到點云空間平移矩陣，接著使用在數據更新前提下的迭代最近點算法(Iterative Closet Point, ICP)算法獲得前后兩幅點云圖像的精確旋轉矩陣與平移向量，實現空間三維數字化重構目標。圖2為結合單線激光雷達和GNSS/INS的系統三維重構工作流程。

圖2 空間三維重構流程Fig.2 Flow chart of spatial three-dimensional reconstruction

3.1 傳感器空間、時間配準

在實驗中將單線激光雷達和GNSS/INS慣性測量單元固定在一起，由于實驗測試的空間場景相對于兩個傳感器的體積較大，在實驗過程中可近似將它視作一個在空間內重心重合的質點，那么GNSS/INS反饋的位置姿態信息亦可視為激光雷達的姿態信息。但是二者之間會始終存在一個由初始狀態決定的角度偏差，若采用直接測量該誤差角度的方案，則會存在較大的測量誤差且該偏角不易測量。針對此問題，在研究系統中運用相對角度不變性的原理——前后狀態下的角度差值為定值，來實現數據的坐標變換，即各軸之間存在的相對空間角位置固定，可將它理解為剛體的轉動，避免了偏角測量的難題，同時簡化了坐標轉換時的計算量，提高了計算效率。

除了傳感器數據在空間上存在角度的偏差，數據在時間上的配準也存在一些問題。激光雷達和GNSS/INS之間數據采集頻率不同，當分別在兩個傳感器上采集數據時，易導致起始信號不一致，使數據錯位。為解決數據的時間配準問題，實驗中借助各傳感器內置的Linux時間戳來獲得起始數據時間，并在MATLAB平臺實現傳感器反饋數據的預處理，從而實現激光雷達極坐標下的角度、距離信息和GNSS/INS航向角姿態參數在時間上的配準。進行數據的插值運算時，對于近似直線運行軌跡，采用線性內插；對于折線運行軌跡，采用多項式或分段樣條內插。為簡化后續處理數據的操作步驟，可在MATLAB內設計一個GUI(Graphical User Interface)將上述步驟程序化，大大提高了數據預處理的效率，節省時間與空間上的資源。

3.2 四元數坐標轉換與姿態解算

單線激光雷達是對其激光束掃描面的二維信息進行獲取，所以本實驗使用了GNSS/INS增加三個航向角掃描的維度，獲取更多的三維空間信息。為此，需要將在時間上配準的傳感器數據應用四元數進行坐標轉換，結合GNSS/INS采集到的姿態角信息解算出掃描數據點在空間中的坐標位置。

傳感器的姿態解算是實現三維重構的核心技術之一。實驗中，三維重構研究系統的姿態和航向角能夠有效地反映各個時刻下其所在空間的位置，從而繪制在空間某一位置的三維掃描圖像。運用四元數進行姿態解算，能夠減小因航向角分析順序不同而導致的誤差，并解決在某一個航向角的旋轉值為90°時會出現萬向節鎖的問題，最終導致剛體喪失旋轉自由度。隨著捷聯式慣性導航技術的發展，采用四元數法來描述剛體的角運動變得更加簡單方便，四元數因其方程計算量不大、工作效率較高而廣泛應用于描述空間載體的剛性運動。根據GNSS/INS獲取的姿態數據可以得到載體在空間上的姿態信息：pitch(圍繞X軸逆時針旋轉的俯仰角)、yaw(圍繞Y軸逆時針旋轉的偏航角)、roll(圍繞Z軸逆時針旋轉的翻滾角)。圖3表示載體姿態的解算流程。

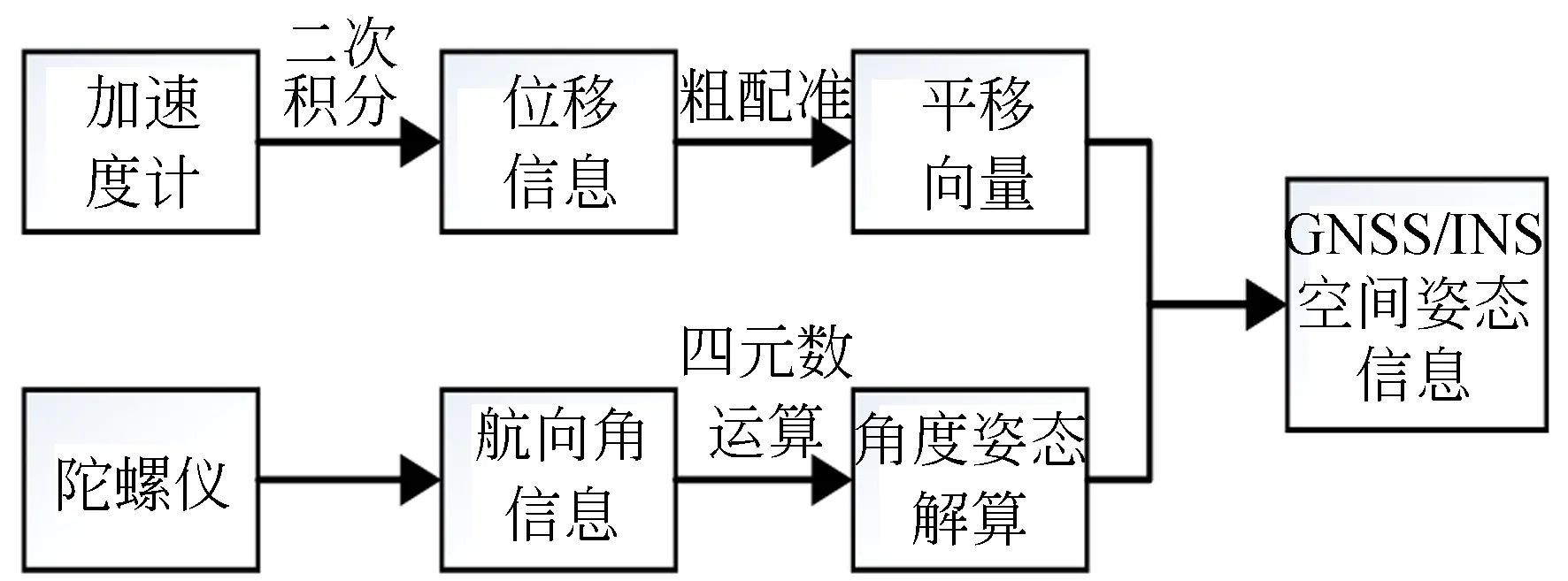
圖3 載體姿態解算流程Fig.3 Vehicle attitude solution procedure

由于單線激光雷達所獲取的數據以極坐標形式展示，為簡化角度在空間上的旋轉運算，對數據進行坐標變換，將極坐標轉化至笛卡爾坐標系內。設激光雷達某一數據點的極坐標為(ρ,θ)，其中ρ為距離值，θ為水平掃描角。為提高掃描空間每一幀點云圖像的可視化程度，在姿態解算過程中將激光雷達起始掃描線旋轉π/4，使兩坐標系下極軸與笛卡爾坐標系下橫軸重合。由于三個角度具有空間對稱性，這里以圍繞X軸即激光雷達的極徑旋轉的俯仰角α為例，說明該數據點的三維笛卡爾直角坐標(x,y,z)：

(1)

在僅存在單一角度旋轉時，此方程的適應性較強，但當三個方向均存在旋轉角度時，對各個方向的角度運算順序會對實驗結果產生比較大的影響，會出現一組角度對應多個空間點，尤其是當其中的一個繞軸旋轉角度為π/2時，會出現萬向節鎖，導致其中兩個軸發生重合，進而失去一個自由度的情形。

為了避免萬向節鎖的出現，應用四元數刻畫其繞任意軸的旋轉。Faugeras和Hebert[12]應用四元數算法來處理移動物體的配準問題。四元數是一種高階復數，單位四元數是一個包含4個矢量的列陣，即有：

qR=[q0,q1,q2,q3]T,

(2)

四元數對航向角的運算過程為：

q=Rq′，

(3)

其中:R代表四元數航向角的旋轉矩陣，q′是作用旋轉矩陣前的掃描數據點在空間的坐標，q是原始數據運算四元數旋轉矩陣后的結果。空間掃描數據任取一點p，設p點繞x軸、y軸、z軸的旋轉角度分別為α，β，γ。那么四元數內繞x軸、y軸和z軸的旋轉矩陣將可以表示為：

(4)

(5)

(6)

由各個軸向的旋轉矩陣，在空間上任意航向角的旋轉可由以上矩陣復合得到點云數據的旋轉作用矩陣。

4 點云圖像配準

點云配準是點云數據處理的關鍵技術之一，其實質是確定點云間的變換參數，從而將不同掃描坐標系下的點云轉換至全局坐標系下，實現空間三維重構。運用四元數進行姿態解算后，實驗中需要將位于局部坐標系的點云圖像轉化到全局坐標系內實現點云配準，進而獲得空間三維重構的效果。鑒于采集的數據圖像在時間上是連續的，故可將點云圖像劃分為多幀圖像實現配準。定義前幀數據上的任意一點在全局坐標系下的坐標記為pn=[xn,yn,zn]T，當前幀數據上的任意一點在全局坐標系下的坐標為pn+1=[xn+1,yn+1,zn+1]T。pn到pn+1的三維旋轉矩陣R和平移向量t為外部參數矩陣，它們的轉換關系如下：

pn+1=R*·pn+t,

(7)

其中：R*·pn表示矩陣R中的元素與矩陣pn中的元素按照相同位置進行相乘，得到的結果作為新矩陣中相同位置的元素。其中，旋轉矩陣的變換表現為空間剛體變換，將源點云變換到目標點云相同的坐標系下。

4.1 迭代最近點算法與數據更新

ICP算法[13]主要用于實現多視角下的數據配準。ICP算法是一種高效的三維配準算法，普遍應用于激光雷達掃描數據處理。初代ICP算法可以概括為以下幾個步驟：

(1)根據點集pn中的點坐標，在統一曲面S上搜索相應最近點點集pn+1；

(2)計算兩個點集的重心位置坐標，點集中心化生成新的點集；

(3)由新的點集計算正定矩陣N，進而得到矩陣N的最大特征值及最大特征向量；

(4)由于最大特征向量等價于殘差平方和最小時的旋轉四元數，將四元數轉化為旋轉矩陣R；

(5)確定旋轉矩陣R后，通過兩個坐標系中的重心點確定平移向量；

(6)以連續兩次距離和之差的絕對值作為迭代判斷閾值；

(7)執行迭代過程直到滿足閾值條件。

ICP算法具有較高的配準精度，但同時存在運算量較大、效率低等問題。其主要原因是ICP算法處理的數據量較大且數據是連續的。為了減少在查找最近點時耗費的時間，本文首先利用k-d tree[14]提高數據查找速度，并基于八叉樹的空間坐標分割管理數據存儲結構。通過松散八叉樹數據結構管理場景節點，進行可見性數據分割，可有效減少數字信號傳遞的數量，且對于連續點云圖像配準通過時間維度上的掃描數與角度分割數據，即間斷性地配準點云數據。這樣不僅可以保留點云的數字特征，而且在配準時也可以有效減少算法的運算量。

4.2 加速度積分粗配準

通過GNSS/INS中的加速度計可以得出在空間坐標系下的各個方向的加速度值，對加速度數據施以二次積分運算即可得到傳感器的位移變化量，但是此過程中易出現二次趨勢的問題，在此使用低通濾波滾動平均值的方法將一些低頻信號去除。實驗中傳感器的頻率為中頻振動，在此選用頻域積分來獲取位移量。

圖4 采集數據場景Fig.4 Data acquisition scenarios

4.3 實驗及結果

為了驗證本文提出的空間三維重構方法的可行性，實驗選擇200 mm×200 mm×300 mm的立方體作為實驗數據采集對象；實驗數據處理平臺為i5-4200M cpu，8 GB內存，win7操作系統。如圖4所示，利用GNSS/INS收集的多維歐拉角信息和單線激光雷達數據，可以得到兩組未配準的圖像。

單線激光雷達在俯仰方向上進行50幀掃描。將這50幀的點云數據結合GNSS/INS提供的俯仰角進行坐標轉換，轉移到同一坐標系下。由于每幀數據轉換算法在步驟上是相同的，所以每組圖像都需迭代50次，如圖5(a)所示。然后，通過ICP算法實現旋轉矩陣和平移向量測量，結果如圖5(b)所示。

作為比較，利用16線激光雷達VLP-16實現相同的過程，結果如圖6所示。多線激光雷達的三維構造過程可以更均勻地分布點數據，并且比單層激光雷達具有更詳細的構造效果。表2是實驗過程中的點云數量以及其處理時間。多線激光雷達比單線激光雷達消耗更多的時間，消耗的時間約為單線激光雷達的5倍。

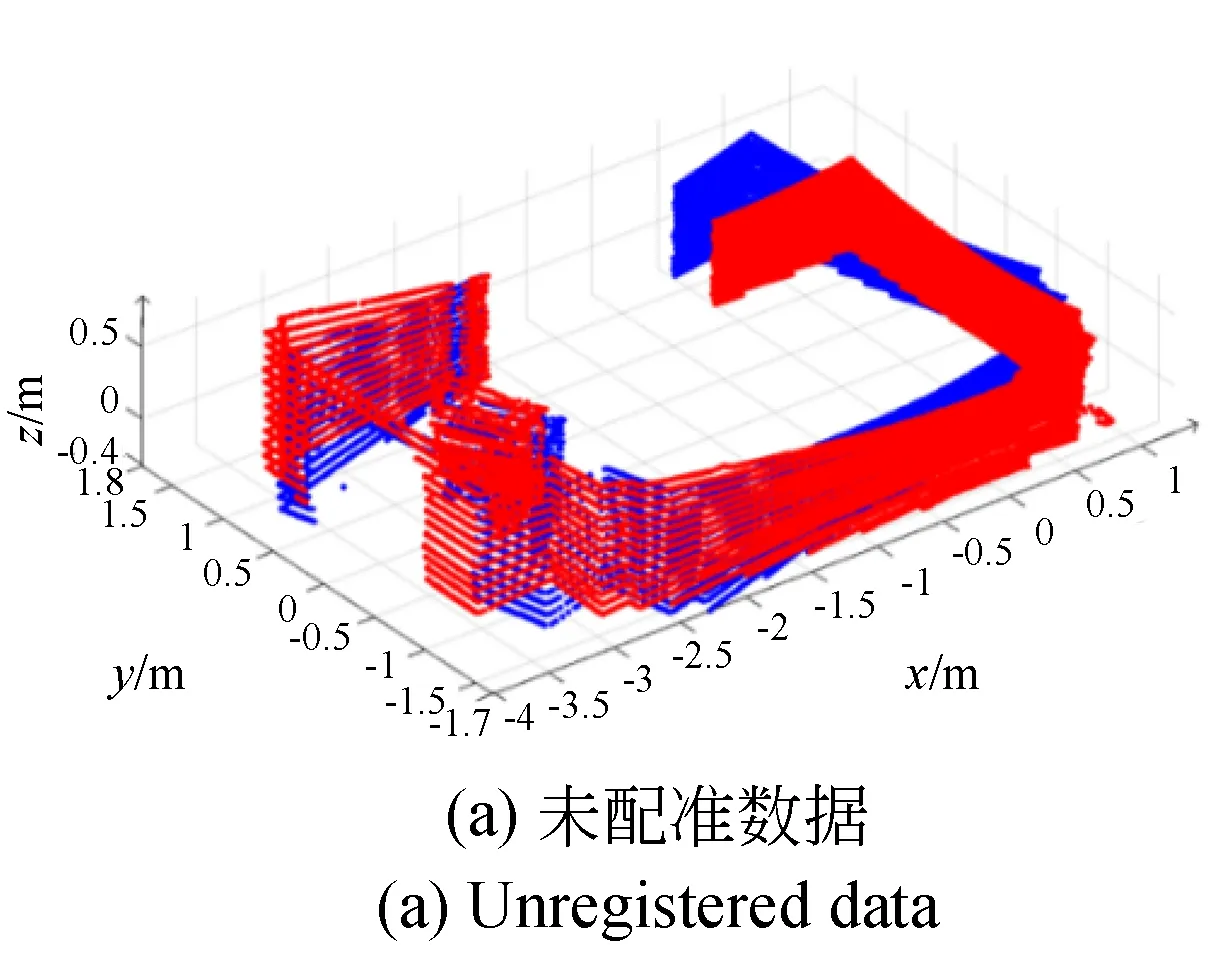
圖6 多線雷達數據處理后的結果

Fig.6 Processed results of multi-layer LIDAR

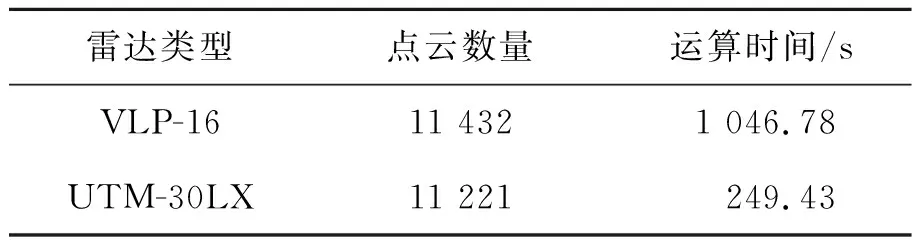
表2 點云數量與運算時間

表3是結合ICP算法所得到的各自點云數據配準所需的旋轉矩陣與平移向量。為了精準地對單線激光雷達與多線激光雷達的配準精度進行量化對比，引入ICP配準評價指標[15]，其計算公式如下：

(8)

其中：Lpi是源點云中對應原始點的最優配準點，Iqi為Lpi的最近鄰點。首先計算配準后對應點云之間的歐氏距離，再對得到的所有數值求和后除以配準點總數進行平均，得到的平均距離差值即為ICP配準評價指標Q。配準評價指標數值越小，配準效果越好。在本文實驗環境下，當Q<0.3時，配準精度較高。

表3中數據代表了單線激光雷達和多線激光雷達重構比較過程中的準確性。結合上述的ICP配準評價指標，可以得到單線激光雷達的重構配準精度較好，且與多線激光雷達效果接近。

表3 點云配準旋轉矩陣、平移向量以及配準得分

5 結 論

本文詳細闡述了單線激光雷達和GNSS/INS的空間三維重構技術，并在實驗中驗證了這一系統在空間重構方面的可行性。利用相對角度不變性原理，解決了單線激光雷達與GNSS/INS相對角度偏差的問題。并且，利用四元數對激光雷達的點云數據進行坐標轉換。結合GNSS/INS的姿態角度信息，完成姿態解算，獲得空間點云圖像。在本文實驗環境下，根據ICP配準的評價指標可以得到單線激光雷達與多線激光雷達的配準得分較為接近，單線激光雷達與GNSS/INS的空間三維重構系統與多線激光雷達構成的三維重構系統同樣具有較高的配準精度。使用ICP算法進行點云空間配準時，利用k-d tree方法提高數據篩選速度，并且結合八叉樹的空間坐標分割管理數據存儲結構特征，對待匹配的點云數據進行更新。在保留點云數字特征的前提下，能夠顯著提高運算速率。實驗結果表明，本文提出的基于單線激光雷達結合GNSS/INS的方法，相較于多線激光雷達方法可以節省76%的數據處理時間，而且單線激光雷達與GNSS/INS的空間三維重構系統在俯仰方向上得到的角度范圍更大且垂直角度分辨率也是可控的，可以針對特定感興趣區域通過增加俯仰角度測量范圍以及縮小垂直角度分辨率，使得數據更加詳細、均勻。本文方法能夠在某些領域的三維空間重構中替代多線激光雷達。