“問”之到位，“引”其深思

陳華忠

數學教學就是培養學生善于思考、懂得思考，而問題就是學生思考的助推器。教學時，我們要以問題為主線，打開啟迪學生思維的大門，驅動學生積極思考。那么，如何做到“問”之到位、“引”其深思呢？

一、抓住問的對象，激發學生思考

一節課的教學內容往往包含了許多數學知識點，可以設置許多問題，但有質量、有價值的問題才能夠問到學生的心坎上，激起思維的漩渦。有價值的問題有助于學生各抒己見，也能激起學生思考的熱情。為此，問題的設計和挑選至關重要，應依據教學重點、難點，依據學生實際情況，為學生學習數學服務，促進學生積極思考。

1.研讀教材。能否精準地掌握教材的核心內容和教學的核心目標是設置問題的關鍵點。因此，教師要認真分析教材，對多個知識點進行剖析，合理地確定教學重點、難點，從中確定有價值的問題。也可把整節課的問題一一羅列出來，進行分析、梳理、篩選、整合，提煉出核心問題。

2.了解學生。不容置疑，學生才是課堂教學的主體。正確地預測學生當前的知識發展水平是設計問題的出發點。首先，客觀、全面地對學生的學習起點和學習需求進行剖析，包括原有的知識程度、技能和學習動機、興趣等，以此來設計問題。其次，教師在備課時可以這樣思考：（1）要讓學生學些什么？（2）如何能引發學生學習這個內容的需求？（3）如何讓學生透徹地理解這個內容？以換位思考的思路來設計問題，突出了學生的主體地位，有利于發展學生的思維能力。

二、抓住問的時機，促進學生思考

好的問題有利于激發學生去思考、去探究。但若問的“點”不到位，學生往往是一頭霧水。若能把握住問的時機，激發學生去探究、去討論、去交流，就能有效地促進學生積極思考、主動探究。

1.問在認知沖突處。“學起于思，思源于疑。”為此，當學生在學習過程中出現困惑與問題、產生沖突與分歧時，教師要抓住時機，適時發問，定能收到良好的教學效果。

例如，在教學“統計”一課時，教師讓學生根據某市11月天氣情況的統計表完成統計圖時，一個學生忽然喊道：“老師，一格能不能代表4天？”其他學生都驚奇地看著他。

師：好問題，這里的一格能否代表4天呢？大家議一議。

在一片討論聲后，學生紛紛發表了自己的看法。

生1：一格可以代表1天，也可以代表2天，還可以代表4天。

生2：若一格代表4天，那陰天有10天，在統計圖中怎么畫？

生3：我覺得要是一格代表4天，那陰天有10天，可以畫兩格后再畫半格。

師：說得很好，在統計圖中一格可以表示一個單位，也可以表示兩個單位，還可以表示3個單位、4個單位或更多的單位，當不夠一格時可以用半格來表示。

學生不經意地提出一個問題時，教師順勢抓住這個與核心內容相關的問題，讓學生展開討論交流，從而加深對統計知識的理解，并將學生的思考引向深處。

2.問在思維閃光處。課堂上學生往往會涌現出新的想法、新的見解。這時，教師要抓住機會，巧妙引領，適時發問，引導學生去思考、去探究。

例如，一位教師在教學“用數對確定位置”一課時是這樣處理的：

師：下面的照片中，哪一個是張老師的女兒？能用以前學過的方法大膽猜測一下嗎？

（學生猜測照片。）

師：如此看來，光靠猜，不可能很快確定張老師女兒的位置，那么，老師提示她是在第3組。（板書：第3組。）

生1：我知道了，是第3組第4個。

生2：不對，第3組有好幾個女生，這樣還是不明確，還得知道是第幾個。

（師補充板書：第2個。）

生3：找到了，是她！

師：看來，我們學過的方法，還真能幫助咱們很快地確定一個人的位置。若是換個角度看，除第3組第2個之外，還可以怎么表示她的位置？

生4：第2排第3個。

生5：為什么同一個位置有兩種說法？應該有統一規定嗎？

師：這就是我們今天要研究的問題：怎樣才能統一、簡明地確定位置？

為此，教學時教師要善于抓住好的問題，恰到好處地發問，觸發學生深度的思考與探究，經歷從多樣表達到規范表達的優化過程。

3.問在知識延伸處。在數學課堂教學中，教師如果能夠調動學生多角度思考，啟發學生質疑問難，對知識進行合理延伸，就可以更好地引導學生思考，為學生能夠在更高層次領悟數學知識架設起階梯。

如在教學“重疊問題”一課時，教師在鞏固練習中設計這樣一道題：甲文具盒有7種文具，乙文具盒有5種文具，文具種類可以自由選擇，問：兩個文具盒中一共可能有多少種文具？你能畫出圖來嗎？通過這道題學生體會到，兩個集合之間除了能出現交集的情況外，可能出現沒有交集的空集情況，還可能出現一個集合完全包含在另一個集合中的子集情況。簡單的素材，多維的應用，深化了概念的內涵，擴展了知識的外延，培養了數學思維。

4.問在學生錯誤處。學生在學習過程中難免會出現錯誤，此時，教師若能發現錯誤的價值，利用錯誤資源，適時發問，促使學生的思維逐步走向深入，可以獲得更好的學習效果。

例如，在教學“分數的意義”一課時，教師出示這樣一道題：

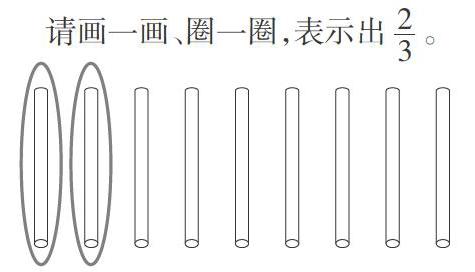
展示作品時，看到一個學生這樣畫：

這時候，教師不急于評價，而是讓這個出錯的學生說說是怎么想的？

生1：不是要表示其中的兩份嗎？所以，我就這樣圈了。

師：這樣表示是正確的嗎？誰來幫幫他。

生2：不對的，他是表示出了這樣的兩份，但這兩份有多少，不明確。

生3：在表示這樣的兩份前，要先確定平均分成3份，每一份是多少，才知道兩份有多少。

生4：我認為要先確定誰是單位“1”，把誰看成一個整體，然后再平均分成3份，取這樣的兩份。

……

教學中，面對學生出現的錯誤，教師以問題反問，引導學生交流討論，進一步內化單位“1”的概念。學生在糾錯、改錯中感悟道理，融會貫通。

（作者單位： 福建省福清市岑兜中心小學）