巧設問題，打造數學技能教學課堂的美

江古月

【摘要】問題是數學的心臟，一個好的課堂問題的提出，內涵豐富，在問題解決的過程中可以讓學生獲取知識，提高能力。數學操作技能課的教學往往通過老師講解，學生模仿和練習，也能把這個技能教給學生，但是從學生實際掌握的效果來看，情況并不十分理想。作為一線教師應該關注兒童，通過問題驅動，設置完整的問題鏈，來調動學生學的興趣。

【關鍵詞】問題;技能教學;學習興趣

“根據方向和距離在平面圖上表示物體的位置”是蘇教版小學數學六年級下冊“確定位置”單元第二課時的內容，在第一課時的教學中，學生已經初步學會了用方向和距離描述物體位置的方法，因此在平面圖上表示物體的位置并不會有太大困難，同時這也是一種基本的操作技能。但是作為一節公開課，要求會更高一些。老師們在平時的培訓學習中也很少聽到這樣的技能教學課，因為這樣的技能教學容易降低學生的思維水平，孩子們缺少思考與探究，更缺少猜想與創造，所以老師們都不愿意選擇這樣的課堂進行公開展示。是不是這樣的內容就不重要呢？顯然不是。如何建構學生的知識體系，培養學生的空間觀念，讓學生從形式模仿走向真正的意義建構，筆者在教學中進行了初步的實踐和思考。

一、生活問題，激活已有知識經驗

【片斷一】

師：陽春三月，正是我們揚州的旅游旺季，為了便于游客游玩，我們可以繪制一幅揚州景點平面圖。

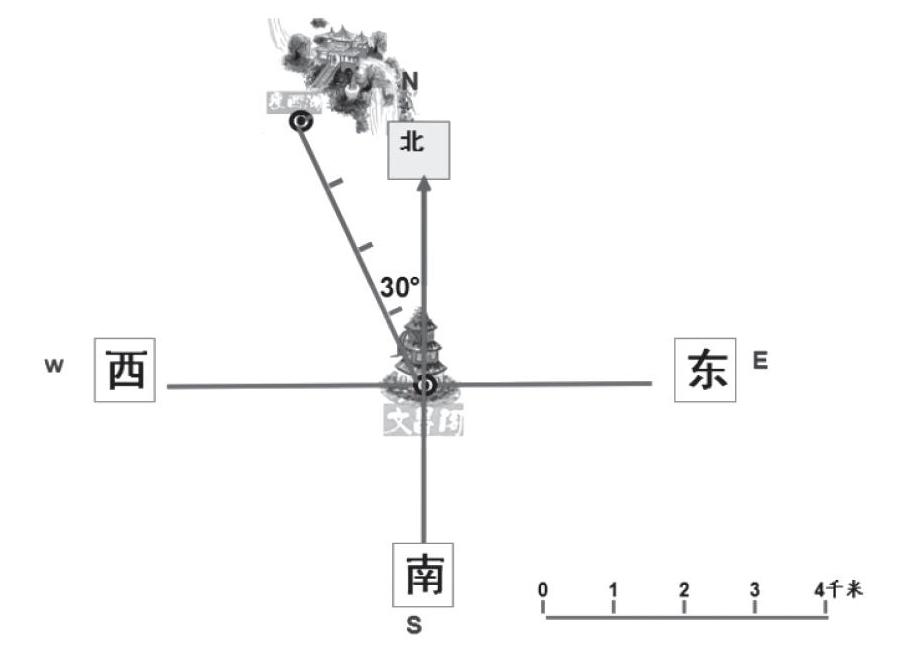
師：文昌閣是揚州的地標建筑，如果以文昌閣作為觀測點，最受歡迎的瘦西湖，在地圖上的位置誰能來介紹一下？

生：瘦西湖在文昌閣的北偏西30 °方向4千米處。

引導復習一：我們上節課學過的4個方向：北偏東，北偏西，南偏東，南偏西，它們都是以正北和正南為基準來確定方向的。

引導復習二：度數是怎么看出來的？是這條射線與正北方向的夾角。

引導復習三：距離又是如何確定的？關注比例尺和圖上的距離。

總結：在平面圖上，我們要準確描述物體的位置，需要知道三要素——方位、角度以及應用比例尺計算出的實際距離。這是我們之前學習過的一種從面到線再到點不斷精確地確定位置的方法。

反思：當學生面對新的數學問題時，教師能從現實生活中挖掘好的問題“原型”，找到數學知識本身的“影子”，幫助學生回憶與新知學習相關的已有知識經驗，再呈現給學生，那么學生的感知肯定會很深刻。上述教學中，筆者沒有沿用教材中某海域島嶼圖，而是采用了繪制家鄉揚州的景點平面圖的情境，更貼近學生的生活，激發學生的學習興趣，激活學生原有的知識經驗。教師提出問題：“瘦西湖在地圖上的位置誰來介紹一下？”重點復習三個方面：一是大概區域可以用北偏東、北偏西、南偏東、南偏西來表示;二是角度如何確定;三是距離如何確定。“面— 線—點”的深化過程，讓學生感受到在平面圖上表示物體位置時也是按照這樣的思考順序，這是對舊知的復習，同時也是為新知打下基礎。顯然，這樣的復習是很有必要的，通過問題情境的設置，將數學知識點巧妙應用在生活中，融會貫通。

二、探究問題，提升問題解決能力

【片斷二】

師：如果以文昌閣作為觀測點，想在這幅圖上表示出東關街的位置，你需要知道哪些信息呢？

生：方向、角度、距離。

師：要想準確畫出它的位置，我們需要準備哪些工具？有可能會遇到什么問題？和你的同桌商量一下。

生：量角器、直尺。

生1：我覺得在畫圖前應該要先確定它的大概位置。

生2：畫的時候角度不能量錯了。

反思：華應龍老師執教過“角的度量”一課，也是一節數學技能教學課，他提出一些思考：為什么教得那么累？傳統的技能訓練課怎么上？技能訓練課的意義在哪里？總的來說還是要讓學生了解知識間的聯系。本節課上，筆者沒有直接告知學生我們怎么去確定物體的位置，而是先讓學生通過交流，提出問題：“要想表示東關街的位置，我們需要知道哪些信息？需要準備哪些工具？”這應該是操作技能課所必備的基礎。要讓學生感知到今天的新知和以前的操作練習有什么不一樣的地方，從信息收集到工具準備，這些都應該是我們的關注點，這些都伴隨著學生的成長與進步。

三、核心問題，有效突破教學難點

【片斷三】

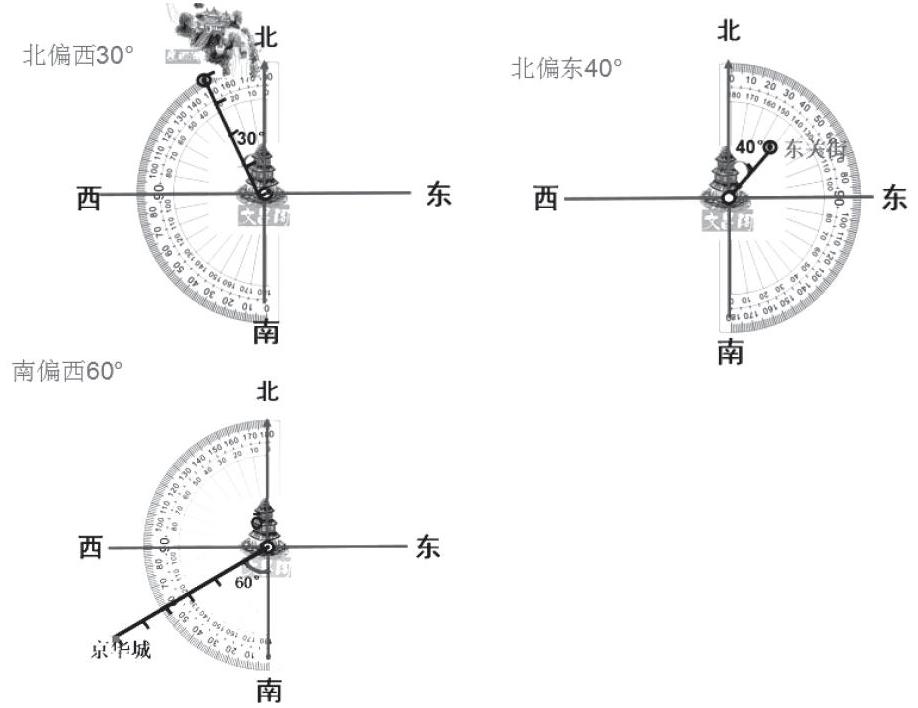
課件出示三幅圖。

師：仔細觀察三幅圖上量角器的擺放，你發現了什么？

生：我發現量北偏西、南偏西時，量角器的半圓部分都是放在左邊，而量北偏東、南偏東時，量角器的半圓部分都是放在右邊。

師：北偏東和南偏東擺放位置是一樣的，量角度時也是一樣嗎？

生：不一樣。量北偏東的角度時，看量角器外圈刻度，0刻度線對準正北方向;量南偏東的角度時，看量角器內圈刻度，0刻度線對準正南方向。

師：看來，在確定角度時，量角器的擺放也是很有講究的。

反思：課堂教學問題的提出首先要立足于知識本質，體現教學內容的重點，能夠引導學生去思考，引領學生自主探究，最終能夠突破教學的難點。通過幾次試教，筆者發現學生的易錯點就在畫角度環節。如何突破這一難點？“仔細觀察三幅圖上量角器的擺放，你發現了什么？”通過這一問題的提出，使問題的聚焦點集中在量角器的擺放上，呈現出三個量角器的對比擺放，學生很容易發現其中的異同：北偏西、南偏西量角器擺的位置都是一樣的，但是要找到不同的0刻度線，表示北偏東、南偏東也是同樣的道理。教師通過對比演示，以及核心問題的提出，將多種表達方式有機整合，巧妙化解教學難點，讓學生善于觀察，善于發現，思維走向成熟。一個問題的提出要以激發學生解決的需要為突破口，并在興趣的激勵下，通過自主探索去掌握新知識，引領學生深度學習，促進學生數學素養的形成。

四、“誘錯”問題，提升學生思維水平

【片斷四】

出示揚州景點平面圖，引導學生根據提示尋找目標位置。

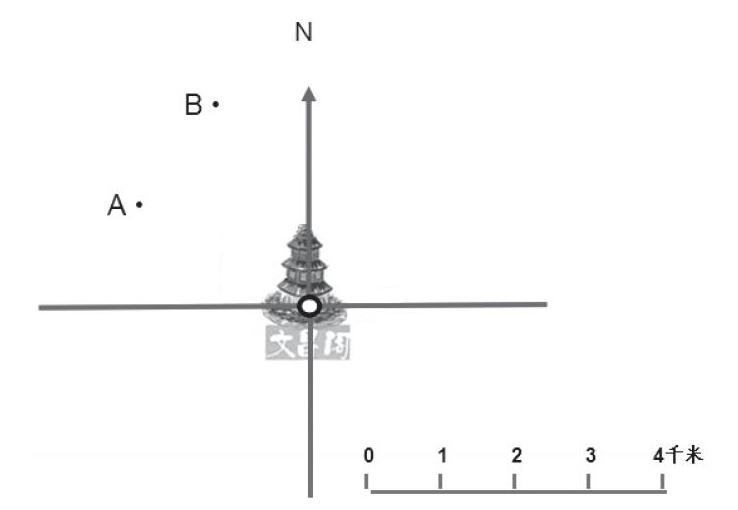
出示目標1在文昌閣北偏西 60°方向 3千米處。

師：哪一個位置是目標1呢？

生：A那個點。

師：你是怎樣想的？

生：目標1在文昌閣的北偏西，因此只有A點和B點，而A點的位置大概就是 60°。

師：你們能驗證自己的想法嗎？

學生用量角器在作業紙上操作驗證。

出示目標 2在北偏東 15°方向2千米處。

師：簡單，北偏東15°嘛，肯定是C點。和老師想法一樣的舉手。

（大部分學生紛紛舉手）

師：有沒有其他意見？你還有問題需要提出來討論嗎？

生1：老師是不是給咱們設陷阱啊？肯定是C點嗎？會不會有其他可能？

生2：目標2是不是在文昌閣的北偏東 15°方向2千米處？

生3：題目上面沒有明確說。

生4：老師，我有疑問，請問目標2是在誰的北偏東 15°方向2千米處？

題目重新出示：目標 2在目標1的北偏東 15°方向2千米處。

（生恍然大悟，開始討論）

生5：我覺得是B點。C點的位置是在文昌閣的北偏東15°方向，而題目中目標 2是在目標 1的北偏東 15°方向，我們觀察的點是目標1，而不是文昌閣，所以我覺得是B點。

生6：目標 1是在文昌閣的北偏西 30°，而目標 2的位置在目標 1 的北偏東 15°，二者的觀測點不同。

師：看來，確定位置的時候還要注意觀測點。這也是一個很重要的信息。

反思：張興華老師在《兒童學習心理與小學數學教學》一書中指出：“學生思維的開啟需要各種刺激和誘因，而各種刺激和誘因中最有價值的莫過于由疑問引起的思維。質疑是思維的導火索，是學習的內驅力，它能使學生的求知欲由潛伏狀態轉入活躍狀態。”由于本節課教學重點是用方向和距離確定物體的位置，學生的關注點很容易就放在方向和角度上，而忽略了觀測點這一重要信息。“有沒有其他意見？你還有問題需要提出來討論嗎？”讓學生學會質疑，學會反思，提高了學生的問題意識。通過讓學生尋找目標點，將枯燥的練習變得充滿生機活力，“這太簡單了，肯定是C點呀”，教師故意誘錯，引學生“上當”，風趣幽默的同時更多的是給學生帶去思考與質疑。經過孩子們的這番爭論，點燃了他們的思維火花，使之產生好奇，再逐步引導孩子們對問題進行分析、解決。整個過程中，生生之間通過交流、質疑，獲得了屬于自己的成功與滿足，令人印象深刻。數學課堂注重學生的思維訓練，教師也渴望在課堂上聽到不一樣的聲音，因為這些聲音，才是學生真正自主思考的呈現;如果沒有這些聲音，完全聽由老師講學生聽，那樣的課堂就猶如一潭死水，沒有半點生機。

數學課堂上，無論是老師提的問題，還是學生提的問題，都是鮮活的資源，都要靜靜思考，師生共同進步，迸發思維的火花。孩子們體驗數學、經歷數學的學習才是理解性的學習，這樣的課堂才是本真的、充滿活力的課堂。

【參考文獻】

[1]史厚勇.引領思維沖突 完善自我建構[J].中小學教學研究，2014（6）.

[2]郜曉定.從粗略到到精確[J].小學數學教育，2017（5）.

[3]張興華.兒童學習心理與小學數學教學[M].江蘇教育出版社，2011.