小學(xué)數(shù)學(xué)教學(xué)數(shù)形結(jié)合思想的運(yùn)用芻議

摘要：數(shù)形結(jié)合思想整合應(yīng)用于小學(xué)數(shù)學(xué)教學(xué)，有助于學(xué)生理解和掌握數(shù)學(xué)知識;提高問題解決能力和數(shù)學(xué)思維能力。小學(xué)數(shù)學(xué)教師要巧用數(shù)形結(jié)合思想，將數(shù)學(xué)教學(xué)中兩個重要的元素“數(shù)”與“形”有機(jī)整合起來，實(shí)現(xiàn)“以數(shù)解形”和“以形助數(shù)”的教學(xué)目標(biāo)。

關(guān)鍵詞：小學(xué)數(shù)學(xué);數(shù)形結(jié)合思想;應(yīng)用對策

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》明確指出：數(shù)形結(jié)合思想是重要的數(shù)學(xué)思想方法，貫穿于數(shù)學(xué)教學(xué)的始終。數(shù)學(xué)作為一門研究空間形式和數(shù)量關(guān)系的自然科學(xué)，“數(shù)”與“形”是數(shù)學(xué)教學(xué)中兩個極其重要又極其古老的元素。“數(shù)”與“形”的有機(jī)結(jié)合，即數(shù)形結(jié)合，將“數(shù)”的嚴(yán)謹(jǐn)性與“形”的直觀性有機(jī)整合起來，打破了數(shù)學(xué)教學(xué)中數(shù)與形的隔閡而實(shí)現(xiàn)完美統(tǒng)一，是構(gòu)建“以數(shù)解形”和“以形助數(shù)”教學(xué)目標(biāo)的有效途徑。對小學(xué)生而言，數(shù)形結(jié)合不僅是一種重要的數(shù)學(xué)思想方法，更是學(xué)生解決問題的關(guān)鍵。教師在小學(xué)數(shù)學(xué)教學(xué)中，要巧妙地借助數(shù)形結(jié)合思想的運(yùn)用，實(shí)現(xiàn)數(shù)與形的相互補(bǔ)充和相互轉(zhuǎn)化，培養(yǎng)學(xué)生數(shù)學(xué)思維，提高數(shù)學(xué)學(xué)習(xí)質(zhì)量。

一、 數(shù)形結(jié)合思想的內(nèi)涵

數(shù)學(xué)學(xué)科有兩個主線：數(shù)學(xué)知識是明線，而數(shù)學(xué)思想是暗線。數(shù)學(xué)思想是對數(shù)學(xué)知識的概括和總結(jié)，并蘊(yùn)含在數(shù)學(xué)知識的發(fā)生和發(fā)展中。數(shù)學(xué)思想是對數(shù)學(xué)知識和數(shù)學(xué)本質(zhì)的概括和抽象，是數(shù)學(xué)的靈魂，對學(xué)生理解和掌握數(shù)學(xué)知識、數(shù)學(xué)規(guī)律等具有較強(qiáng)的應(yīng)用價值。

數(shù)形結(jié)合思想是重要的數(shù)學(xué)思想方法。著名數(shù)學(xué)家華羅庚曾說;數(shù)與形相輔相成，永不分離，并提出了“數(shù)形結(jié)合萬般好，隔離分家萬事休”的重要理論。那么，何為數(shù)形結(jié)合思想呢？筆者認(rèn)為：所謂數(shù)形結(jié)合思想，就在數(shù)學(xué)教學(xué)中，將抽象的數(shù)量關(guān)系與直觀的空間形式有機(jī)整合起來，充分發(fā)揮“數(shù)”與“形”在數(shù)學(xué)中的優(yōu)勢，并通過兩者的相互結(jié)合和相互轉(zhuǎn)化來解決數(shù)學(xué)問題。數(shù)形結(jié)合思想的運(yùn)用具有明顯的優(yōu)勢，學(xué)生可以不再拘泥于問題的直接表現(xiàn)形式，而可以通過數(shù)與形的結(jié)合，將抽象思維和形象思維有機(jī)結(jié)合，促使復(fù)雜的問題簡單化，抽象的問題具體化，提高教學(xué)質(zhì)量。

二、 小學(xué)數(shù)學(xué)教學(xué)中數(shù)形結(jié)合思想的教育價值

（一）有助于學(xué)生對數(shù)學(xué)知識的理解和掌握

小學(xué)生心智尚在發(fā)展，而數(shù)學(xué)知識則具有較強(qiáng)的系統(tǒng)性、嚴(yán)謹(jǐn)性和抽象性。小學(xué)生在數(shù)學(xué)學(xué)習(xí)中，要想充分掌握教材所呈現(xiàn)的全部知識點(diǎn)，具有一定的難度。那么，如何讓理解能力、思維能力尚在發(fā)展的小學(xué)生輕松地理解數(shù)學(xué)知識呢？我們知道：基于教育改革的需要，小學(xué)生要進(jìn)行有意義的學(xué)習(xí)，不能單靠死記硬背，這種純粹記憶數(shù)學(xué)符號和數(shù)學(xué)公式的學(xué)習(xí)方式是機(jī)械的，學(xué)生難以理解其中蘊(yùn)含的數(shù)學(xué)本質(zhì)。而要實(shí)現(xiàn)學(xué)生充分理解數(shù)學(xué)符號蘊(yùn)含的數(shù)學(xué)內(nèi)容，如數(shù)學(xué)概念、運(yùn)算原理以及規(guī)則等，則需要一定的數(shù)學(xué)思想方法。

數(shù)形結(jié)合思想整合應(yīng)用于小學(xué)數(shù)學(xué)的教學(xué)，則是幫助學(xué)生理解和掌握數(shù)學(xué)知識的重要思想方法。以小學(xué)生學(xué)習(xí)“面積”單位的教學(xué)為例，以往的教學(xué)，我們習(xí)慣于讓學(xué)生背誦單位換算規(guī)則，背誦面積計(jì)算方式，如正方形的面積=邊長×邊長，學(xué)生懂得計(jì)算，但卻不懂得直觀的面積是多少，如一個課桌的面積是多少？教室的面積是多少？學(xué)生都缺乏直觀的認(rèn)知。如教師讓學(xué)生計(jì)算邊長1厘米的正方形面積，學(xué)生都知道面積為1厘米×1厘米=1平方厘米，但1平方厘米有多大呢？如果教師在教學(xué)中，直接讓學(xué)生觀察邊長為1厘米的正方形，學(xué)生能夠直觀地感知1平方厘米有多大，能夠充分感知邊長與面積之間的關(guān)系。這就是數(shù)形結(jié)合的優(yōu)勢所在，能夠讓學(xué)生建立直觀的認(rèn)知，幫助學(xué)生更加清晰地掌握數(shù)學(xué)知識，這就是所謂的有意義的學(xué)習(xí)。

（二）有助于提高學(xué)生的問題解決能力

借助數(shù)學(xué)理論知識解答數(shù)學(xué)問題，是學(xué)生學(xué)習(xí)數(shù)學(xué)知識的目的所在。學(xué)生在解答數(shù)學(xué)問題的過程中，有幾個關(guān)鍵性的步驟：一是審題;二是解題思路。如果學(xué)生通過正確的審題，即對所表達(dá)的數(shù)學(xué)問題有了正確的表征，然后有了清晰的解題思路，那么，其數(shù)學(xué)解題能力將會得到有效的提升。數(shù)形結(jié)合思想應(yīng)用于小學(xué)數(shù)學(xué)的解題，學(xué)生能夠通過“數(shù)”與“形”的相互結(jié)合與轉(zhuǎn)化，表征數(shù)學(xué)題目中的空間形式和數(shù)量關(guān)系，幫助學(xué)生明晰解題思路，提高問題解決能力。例如，數(shù)學(xué)題：學(xué)校為了獎勵表現(xiàn)優(yōu)秀的學(xué)生，買了5箱筆記本，每箱10本，每本10元，一共花多少錢？解答此問題，教師可以巧妙地借助數(shù)形結(jié)合指導(dǎo)學(xué)生理清解題思路：畫5個框代表5個箱子，每個箱子上標(biāo)注10本，一共有50個筆記本，每本10元，一共花費(fèi)就是50×10=500元。這種將題目所表達(dá)的思想“畫”出來的形式，能夠快速地幫學(xué)生將題目中的數(shù)量關(guān)系通過直觀的圖形呈現(xiàn)出來，不僅能夠理清解題的思路，同時還能夠有效地訓(xùn)練學(xué)生的數(shù)學(xué)邏輯思維能力。可以說：在小學(xué)數(shù)學(xué)的教學(xué)中，數(shù)形結(jié)合是幫助學(xué)生準(zhǔn)確無誤地理解數(shù)學(xué)問題、把握數(shù)量關(guān)系的重要思想。尤其是在數(shù)學(xué)圖形教學(xué)中、行程教學(xué)中，教師都可以指導(dǎo)學(xué)生運(yùn)用數(shù)形結(jié)合思想解題，是全面提高學(xué)生問題解決能力的有效途徑。

（三）有助于培養(yǎng)小學(xué)生數(shù)學(xué)思維

科學(xué)研究表明：人的大腦，分為左半腦和右半腦。左半腦擅長抽象和邏輯，更多的是針對“數(shù)”的活動，如歸納、推理等;右半腦則擅長直觀形象，是以“形”為主的活動，如想象活動等。人在思維和思考過程中，需要左右腦同時工作，共同作用;而左右腦同時作用的過程，也就是“數(shù)”與“形”的結(jié)合。這樣的解釋，也許會有些許的牽強(qiáng)，但卻直觀地表明了在學(xué)生數(shù)學(xué)思維的過程中，數(shù)形結(jié)合思想的重要性。筆者認(rèn)為：小學(xué)數(shù)學(xué)教師在教學(xué)中運(yùn)用數(shù)形結(jié)合思想，或者是指導(dǎo)學(xué)生運(yùn)用數(shù)形結(jié)合思想解答數(shù)學(xué)問題，都是培養(yǎng)學(xué)生的數(shù)學(xué)思維的關(guān)鍵。例如，教師在指導(dǎo)學(xué)生學(xué)習(xí)《角的初步認(rèn)識》時，角的直觀概念為“一個頂點(diǎn)，兩條邊”，這是通過嚴(yán)謹(jǐn)?shù)臄?shù)學(xué)語言定義的直觀概念。而教師在教學(xué)中，結(jié)合直觀的圖形，將“一個頂點(diǎn)、兩條邊”的概念表現(xiàn)出來，這種在學(xué)生頭腦中的角的表象化為直觀的圖形，學(xué)生的理解更為清晰。這就是學(xué)生數(shù)學(xué)思維發(fā)生和發(fā)展的過程。反之，教師也可以借助“數(shù)”來表征圖形，實(shí)現(xiàn)數(shù)學(xué)教學(xué)中數(shù)與形的相互轉(zhuǎn)化。由此說：數(shù)形結(jié)合思想運(yùn)用于小學(xué)數(shù)學(xué)教學(xué)，是培養(yǎng)學(xué)生數(shù)學(xué)思維能力的關(guān)鍵。

三、 小學(xué)數(shù)學(xué)教學(xué)中數(shù)形結(jié)合思想運(yùn)用的對策

數(shù)學(xué)學(xué)科具有較強(qiáng)的嚴(yán)謹(jǐn)性、抽象性。小學(xué)生的數(shù)學(xué)思維能力，則是由形象思維逐步過渡到抽象思維。對于小學(xué)生而言，抽象的數(shù)學(xué)知識無疑是晦澀的、深奧的。小學(xué)生在數(shù)學(xué)教學(xué)中，要充分認(rèn)知數(shù)學(xué)知識，需要借助數(shù)學(xué)思想方法，實(shí)現(xiàn)“以數(shù)解形”和“以形助數(shù)”的教學(xué)目標(biāo)。

（一）以形助數(shù)

以形助數(shù)，是數(shù)形結(jié)合思想運(yùn)用于數(shù)學(xué)教學(xué)的重要方面。所謂以形助數(shù)，即在數(shù)學(xué)教學(xué)中，教師通過直觀的“形”解決抽象的“數(shù)”的問題，將復(fù)雜的數(shù)量關(guān)系、抽象化的數(shù)學(xué)問題簡單化、具體化。對小學(xué)生而言，常見的“形”有很多，如生活中的實(shí)物;直角坐標(biāo)系、數(shù)軸、線段圖等。

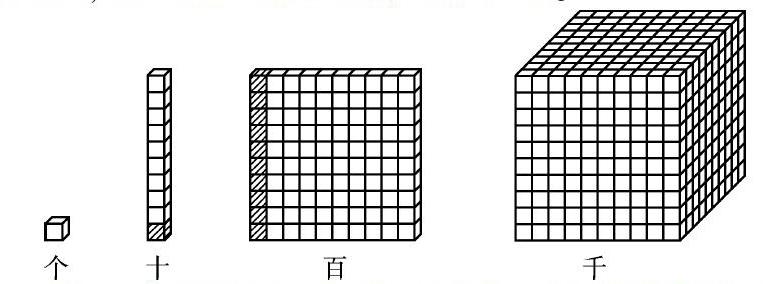
首先，借助形，認(rèn)識數(shù)。借助形認(rèn)識數(shù)，能夠幫助學(xué)生對“數(shù)”的認(rèn)知更為直觀、清晰。讓學(xué)生把握數(shù)的含義，“多”與“少”，“大”與“小”等，讓“數(shù)”的概念在學(xué)生頭腦中的表象更為直觀，且能夠清晰地把握數(shù)與數(shù)之間的關(guān)系。例如，“千以內(nèi)數(shù)的認(rèn)識”教學(xué)，教師借助直觀的幾何圖形，讓學(xué)生直觀地理解什么是“個、十、百、千”，直觀形象地感知“十進(jìn)制”數(shù)與數(shù)之間的關(guān)系，為學(xué)生的數(shù)學(xué)運(yùn)算打下基礎(chǔ)。同時，教師還可以借助生活中的實(shí)物讓學(xué)生理解數(shù)量關(guān)系，如1平方米的面積有多大、一米的長度有多長等。讓學(xué)生借助形，對數(shù)的認(rèn)知更為清晰和直觀。

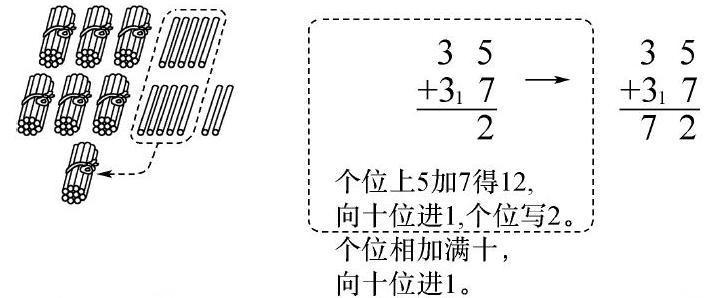
其次，借助形，運(yùn)算數(shù)。數(shù)學(xué)運(yùn)算是數(shù)學(xué)核心素養(yǎng)的組成部分之一，是學(xué)生在進(jìn)行“數(shù)的認(rèn)識”基礎(chǔ)上進(jìn)行的。基于核心素養(yǎng)的視角，小學(xué)數(shù)學(xué)教師在數(shù)學(xué)教學(xué)中培養(yǎng)學(xué)生的數(shù)學(xué)運(yùn)算能力，是發(fā)展其數(shù)學(xué)核心素養(yǎng)的關(guān)鍵。時代在發(fā)展，社會在進(jìn)步，如今，我們對學(xué)生進(jìn)行復(fù)雜運(yùn)算的要求已經(jīng)有所降低，但在教學(xué)中，我們依然要求學(xué)生充分理解數(shù)學(xué)運(yùn)算背后的算理。如學(xué)生對數(shù)學(xué)運(yùn)算定律、運(yùn)算法則的掌握。在低年級階段，指導(dǎo)學(xué)生借助小棒等實(shí)物演示整數(shù)的運(yùn)算定律;借助圖形，如正方形、圓形等對稱圖形把握分?jǐn)?shù)的運(yùn)算法則等，這就是將“形”巧妙地運(yùn)用到“數(shù)”的運(yùn)算中的有效途徑。小學(xué)數(shù)學(xué)教師要善于借助“形”，指導(dǎo)學(xué)生運(yùn)算“數(shù)”，實(shí)現(xiàn)以“形”助“數(shù)”的教學(xué)目標(biāo)。例如，教師在指導(dǎo)學(xué)生學(xué)習(xí)“進(jìn)位加”時，如35+37=？

如上圖，借助小棒，直觀地給學(xué)生展示了“滿十進(jìn)一”的原理，讓學(xué)生對“進(jìn)位加”的認(rèn)知更加清晰，提高了學(xué)生的數(shù)學(xué)運(yùn)算能力。

（二）以數(shù)解形

所謂以數(shù)解形，即在數(shù)學(xué)教學(xué)中，教師借助數(shù)量關(guān)系、數(shù)學(xué)符號、數(shù)學(xué)語言等，詮釋圖形的形式，讓學(xué)生對圖形的理解和認(rèn)知更為精確。

首先，借助“數(shù)”，幫助學(xué)生認(rèn)識圖形。圖形本身如果缺乏“數(shù)”作為支撐，則顯得蒼白。因此，在圖形教學(xué)中，教師要善于指導(dǎo)學(xué)生借助具體的“數(shù)”幫助學(xué)生理解圖形。例如，在小學(xué)數(shù)學(xué)圖形的認(rèn)知中，關(guān)于三角形，我們會用“底、邊、角、高”等語言描述三角形的基本特征，并借助具體的數(shù)量關(guān)系區(qū)分圖形，如直角三角形，有一個角是90°;銳角三角形，三個角都是銳角的三角形叫銳角三角形，而大于0°小于90°的角叫做銳角，等等。此外，教師在教學(xué)中，還可以借助具體的數(shù)字，描述圖形的特征。如在學(xué)習(xí)“長方形”時，用“1、4、4”描述長方形的特征，何為“1、4、4”呢？借助直觀的圖形：長方形有一個面，四個頂點(diǎn)和四條邊。這就是數(shù)學(xué)教學(xué)中“數(shù)”助“形”的途徑之一：幫助學(xué)生認(rèn)知和理解圖形。

其次，借助“數(shù)”，描述圖形的位置和方向，培養(yǎng)學(xué)生的空間觀念。小學(xué)數(shù)學(xué)教學(xué)中，培養(yǎng)學(xué)生的空間觀念，需要教師借助圖形，讓學(xué)生通過了解圖形的位置、方向等，建立距離、角度的直觀認(rèn)知。如“平移”“旋轉(zhuǎn)”等，是描述圖形運(yùn)動的數(shù)學(xué)語言。教師可以借助中心坐標(biāo)系的建立，指導(dǎo)學(xué)生學(xué)會觀察物體的角度，同時懂得比例尺的運(yùn)用，通過比例尺判斷物體的距離等。

綜上所述，小學(xué)數(shù)學(xué)教學(xué)中應(yīng)用數(shù)形結(jié)合思想，即是將數(shù)學(xué)教學(xué)中兩個重要的元素：“數(shù)”與“形”有機(jī)整合起來，借助“數(shù)”抽象概括“形”，借助“形”直觀體現(xiàn)數(shù)，進(jìn)而實(shí)現(xiàn)“數(shù)”與“形”的完美統(tǒng)一，實(shí)現(xiàn)“以數(shù)解形”和“以形助數(shù)”的教學(xué)目標(biāo)，培養(yǎng)學(xué)生數(shù)學(xué)思維，提高小學(xué)數(shù)學(xué)教學(xué)質(zhì)量。

參考文獻(xiàn)：

[1]孫如豐.小學(xué)數(shù)學(xué)教學(xué)中“數(shù)形結(jié)合”的策略[J].新課程學(xué)習(xí)：小學(xué)，2009（4）：126-127.

[2]劉偉.小學(xué)數(shù)學(xué)“數(shù)形結(jié)合”思想方法在教材中的滲透[J].新課程學(xué)習(xí)：基礎(chǔ)教育，2010（8）：93-94.

作者簡介：楊嚴(yán)偉，甘肅省天水市，甘肅省甘谷縣大像山鎮(zhèn)富強(qiáng)路小學(xué)。