插上“隱形的翅膀”，“翱翔”于三角形世界

黃志琴

親愛的同學：看見“三角形”這三個字，你的大腦里會呈現(xiàn)哪些圖形？你想到哪些相關的內(nèi)容與方法呢？梳理三角形的內(nèi)容，使其條理化，或許你覺得三角形很簡單。嘗試先思考以下問題，聯(lián)想知識，再提煉一些方法。

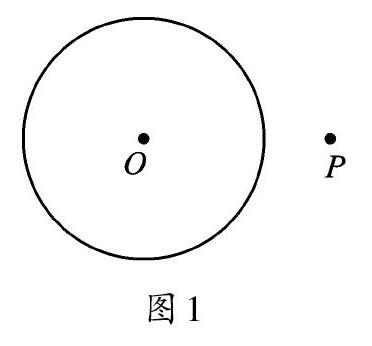
問題1 如圖1，點P是⊙O外一點，請找到圓上一點Q，使PQ最短。

答案見圖2。你能說出道理嗎？跟三角形有關系嗎？

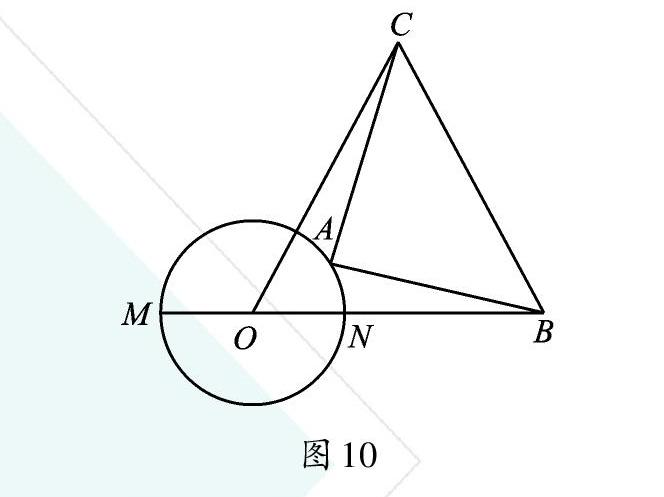
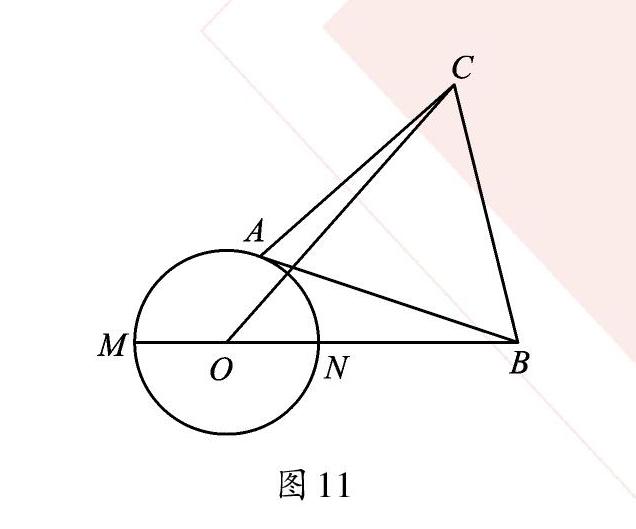
如圖3，在⊙O上任意取點A，連接PA、OA，根據(jù)三角形的性質(zhì)“兩邊之和大于第三邊”判斷PO最小，從而得到圖2中的點Q使PQ最短。這條性質(zhì)的實質(zhì)是“兩點之間線段最短”。三角形是以線段、角等為基礎，卻比線段、角更復雜些的圖形。請聯(lián)想三角形的邊有哪些性質(zhì)，三角形的角又有哪些性質(zhì)。試說明“直徑是最長的弦”，試回答“過圓內(nèi)一點的最短（或最長）的弦是哪一條？為什么？”在圖4中嘗試解答。

三角形這部分知識的應用，還是要從定義及其重要性質(zhì)（邊、角關系）開始，從一般到特殊。這里主要跟同學們聊聊一些隱蔽的三角形和三角形隱含的作用，特別是特殊三角形。

問題2 如圖5，在△ABC中，AB=AC=5，BC=6，將△ABC繞點B逆時針旋轉60°得到△A'BC'，連接A'C，則A'C的長為_________。

同學們，你們覺得此題的突破點可能在哪里？除已知的特殊三角形外，常見的處理辦法是連接CC'得到等邊三角形C'BC（如圖6）。把A'C拆分成兩條線段后分別放在等腰三角形A'BC'和等邊三角形△C'BC中求解。

三角形考查的重點是特殊三角形：等腰三角形、等邊三角形、直角三角形、等腰直焦三角形等。“隱形”三角形是難點，它們還周以“隱形置身”于動態(tài)問題中。把一條線段繞端點旋轉任意角度，連接對應點可以得到等腰三角形。……