電動轉籠二次殘差補償霧化模型建立與試驗

趙春江 柴舒帆 陳立平 張瑞瑞 李龍龍 唐 青

(1.西北農林科技大學機械與電子工程學院， 陜西楊凌 712100； 2.北京農業信息技術研究中心， 北京 100097；3.國家農業智能裝備工程技術研究中心， 北京 100097； 4.國家農業航空應用技術國際聯合研究中心， 北京 100097)

0 引言

航空施藥作業速度快、噴灑效率高、資源利用率高、節能，且應對災害能力強，克服了傳統施藥機械或人工進地作業的難題，受到研究者的高度重視[1-3]。但其離靶目標較遠，在環境、溫濕度和風場等因素的影響下，霧滴粒徑大小會影響飄移情況，造成非靶標區域的人畜污染[4-6]。因此，可控霧滴技術成為國內外航空噴霧技術的研究熱點[7]。

風洞試驗具有模擬真實飛行環境、準確控制風向風速等參數、試驗重復性好等優點[8-10]。目前國內外多采用風洞試驗[11-14]對航空施藥技術進行研究。離心霧化技術通過改變離心霧化器的轉速控制霧滴粒徑，是當前公認的霧滴均勻度較好、霧滴粒譜范圍窄、可供“可控霧滴”之用的先進技術[15]。劉德江等[16]基于最佳粒徑理論，以離心霧化技術為核心，設計了一款可精確控制霧滴粒徑的3WKL-100型遠程可控霧滴噴霧機；龔艷等[17]以離心霧化技術為核心，通過研究離心霧化機理，研發了一款適用性強、可靠性好的遙控式風送變量可控霧滴噴霧機；茹煜等[18]設計了一款無人直升機遠程控制噴霧系統，并得到霧化盤直徑為80 mm的離心霧化噴頭的最佳作業參數。目前國內關于可控霧滴霧化系統的研究多適用于地面機械或無人機[19-21]，難以適應復雜作業環境。

鑒于目前針對農業航空施藥中的大流量轉籠霧化器霧化特性研究較少，且霧化系統環境適應性較差，本文建立一種基于二次殘差補償的霧滴粒徑模型，在風洞實驗室搭建試驗平臺，通過二次回歸正交試驗，建立風速、施藥流速、霧化器轉速與霧滴粒徑間的關系模型，在補償因子修正關系模型的基礎上，利用機器學習對模型殘差進行建模，從而實現模型優化，以得到二次殘差補償霧滴粒徑模型，通過對二次殘差補償霧滴粒徑模型進行等效變形，得到電動轉籠二次殘差補償霧化模型，并基于該模型設計一套電動轉籠霧化系統，實現在恒定風速、施藥流速條件下的霧滴粒徑可控，以期解決航空施藥作業時霧滴粒徑變量精細控制的問題。

1 試驗平臺構建與霧化系統設計

1.1 霧化試驗平臺原理與構成

為了建立霧滴粒徑模型，在北京農業智能裝備技術研究中心自建的IEA-I型航空施藥高速風洞實驗室搭建了一套可精確控制風速、施藥流速與霧化器轉速的霧化試驗平臺，如圖1所示，包括操作臺、藥箱、水泵、風洞、流量計、壓力計、電子調速器、霧化器、粒徑測量儀、計算機和安裝架，其中，藥箱、水泵、流量計和壓力計組成藥液供給模塊。試驗時，風洞模擬航空施藥作業時環境狀態，藥液供給模塊為系統提供設定的施藥流速，計算機通過串口控制電子調速器以調整霧化器轉速，粒徑測量儀測量霧化后的霧滴粒徑，并通過計算機反饋測量值。

圖1 霧化試驗平臺Fig.1 Atomization experiment platform1.操作臺 2.藥箱 3.水泵 4.風洞 5.流量計 6.壓力計 7.電子調速器 8.霧化器 9.粒徑測量儀 10.計算機 11.安裝架

藥液供給模塊中，水泵選用譜羅頓750 W變頻水泵(譜羅頓智控電子科技有限公司)，進出口直徑32 mm，額定揚程25 m，吸程8 m，最大流量2 m3/h，調壓范圍0～0.4 MPa，精度0.01 Pa；流量計選用HSTL-N型渦輪流量計(北京華控興業科技發展有限公司)，其接口直徑10 mm，精度0.5%，工作電壓24 V，量程0.2～1.2 m3/h；壓力計選用HSTL-802型壓力傳感器(北京華控興業科技發展有限公司)，其工作電壓12～36 V，量程0～1 MPa，精度0.1 MPa；藥箱選用白色塑料水箱。本試驗以水作為試驗介質，水泵將水從藥箱吸出經壓力計與流量計從霧化器噴出，壓力計測量管道內水壓，為調壓水泵調整流速提供參考，流量計測量進入霧化器藥液的流速。

風洞的風速范圍6.70～98.00 m/s，試驗段直徑300 mm，動壓穩定性系數小于2%，試驗段湍流度小于1.0%，平均氣流偏角小于0.5%[22]，用于模擬航空施藥過程環境因素。

電子調速器選用Skywalker-40A型空模無刷馬達電子調速器，其額定工作電壓為24 V，額定持續電流為40 A，根據計算機發出的控制信號，調節霧化器的轉速。

霧化器選用Aerial-E型電動轉籠霧化器(北京農業智能裝備技術研究中心)，內置霍爾傳感器可測量霧化器實際轉速，其額定流量10 L/min，極對數13，額定工作電壓24 V，轉速范圍700～8 000 r/min。

粒徑測量儀選用馬爾文激光粒度儀，其工作原理是利用激光的衍射原理，計算檢測器上收集到的不同衍射圖形的光強分布，得到霧滴粒徑與相對分布跨度。通過選擇不同鏡頭可覆蓋0.1～3 500.0 μm的粒徑范圍，實現寬廣的噴霧羽流粒度測試，相對分布跨度是衡量霧滴粒徑分布的指標，其值越大，樣品均一性越低，其計算公式為[23-24]

(1)

式中Dv0.1——全部霧滴以直徑從小到大順序累積，體積累積量等于總體積的10%時,所對應的霧滴直徑

Dv0.5——全部霧滴以直徑從小到大順序累積，體積累積量等于總體積的50%時,所對應的霧滴直徑

Dv0.9——全部霧滴以直徑從小到大順序累積，體積累積量等于總體積的90%時,所對應的霧滴直徑

本試驗中，選Dv0.5和χ為測量參照。

1.2 電動轉籠霧化系統設計

所設計霧化系統原理如圖2所示，主要由計算機、主控制器、風速傳感器、流量傳感器、按鍵輸入模塊、數據存儲模塊、顯示模塊、電子調速器、Aerial-E型電動轉籠霧化器和轉速傳感器組成。Aerial-E型電動轉籠霧化器原理圖與實物圖如圖3所示，主要由分水芯、轉籠、內套管、電機和安裝架組成，安裝架與飛機噴桿連接，藥液進入分水芯，完成液流到液膜的轉變實現一級霧化，電機帶動內套桿與轉籠轉動，液膜進入內套管，完成液膜到大液滴的轉變實現二級霧化，大液滴進入轉籠，完成大液滴到小霧滴的轉變實現三級霧化。系統設定霧滴粒徑后，傳感器模塊測量進入霧化器藥液流速、風速與霧化器實際轉速，主控制器首先設定殘差為0，即根據第1次優化霧滴粒徑補償輸出模型計算霧化器參考轉速，并通過串口將數據傳到計算機，計算機利用建立的第2次殘差預測模型計算殘差量，同時將殘差量通過串口傳輸到主控制器，主控制器再利用電動轉籠二次殘差補償霧化模型計算最終霧化器轉速，利用PI控制算法實現對霧化器轉速調控，實現霧滴粒徑可控，并通過數據存儲模塊與顯示模塊實現對霧化參數的存儲與顯示。利用試驗標定PI控制器參數，標定結果如表1，其中kp為比例增益，ki為積分增益。

圖2 霧化系統原理圖Fig.2 Schematic of atomization system

圖3 Aerial-E型電動轉籠霧化器原理圖與實物圖Fig.3 Schematic and physical of Aerial-E electricity atomizer1.分水芯 2.轉籠 3.內套管 4.電機 5.安裝架

表1 PI控制器參數
Tab.1 PI controller parameter

霧化器轉速n/(r·min-1)kpki700～40000.20.024000～50000.30.035000～60000.40.03

主控制器選用芯片STM32F103VET6，主要完成風速、施藥流速、霧化器實際轉速與按鍵輸入模塊信息的采集，電機與顯示器的驅動及控制算法的執行。

計算機選用戴爾 Optiplex 7010 Mini Tower，其CPU是英特爾第三代酷睿 i5-3470 @3.2 GHz四核，內存4 GB。

直升機施藥作業速度范圍90～160 km/h，風速傳感器選用HSTL-GDFS型風速儀(北京華控興業科技發展有限公司)，工作電壓24 V，量程0～70 m/s，精度等級為3%FS，輸出數據使用RS485協議串行輸出。

Aerial-E型電動轉籠霧化器作業時，施藥流速常規作業范圍7.0～8.0 L/min，流量傳感器選用YF-S201B型渦輪流量計(中江節能電子有限公司)，其工作電壓5～18 V，量程1～30 L/min，精度2%，通過實時采集流量傳感器輸出脈沖計算施藥流速q，計算公式為

(2)

式中f1——流量傳感器脈沖頻率

k——流量傳感器的儀表系數，由北京華控興業科技發展有限公司提供，為35

通過實時采集Aerial-E型電動轉籠霧化器內置霍爾傳感器輸出脈沖數，計算霧化器實際轉速n1，計算公式為

(3)

式中f——速度傳感器脈沖頻率

g——Aerial-E型電動轉籠霧化器轉速比，由北京農業智能裝備技術研究中心提供，為13

數據存儲模塊選用MicroSD卡，其存儲內存8 GB；對施藥過程中霧滴粒徑設定值、施藥流速、電動轉籠霧化器轉速及飛機飛行速度等數據進行存儲。

顯示模塊選用LCD1602(駿顯電子科技有限公司)，其工作電壓3.3 V，用于實時顯示施藥作業參數。

2 二次殘差補償霧化模型建立與優化

電動轉籠二次殘差補償霧化模型技術框圖如圖4所示，利用二次回歸正交試驗分析風速、施藥流速、霧化器轉速與霧滴粒徑間的相關關系，建立霧滴粒徑模型，通過對霧滴粒徑影響因素的分析，添加補償因子對模型第1次優化，得到第1次優化霧滴粒徑補償模型，利用機器學習對第1次優化霧滴粒徑補償模型殘差進行分析，得到第2次殘差預測模型，將其與第1次優化霧滴粒徑補償模型線性疊加得到二次殘差補償霧滴粒徑模型，同時對該模型進行等效變形，得到電動轉籠二次殘差補償霧化模型，并搭建基于該模型的電動轉籠霧化系統。

圖4 電動轉籠二次殘差補償霧化模型技術框圖Fig.4 Quadratic residual compensation atomization model of electricity atomizer

2.1 霧滴粒徑模型

航空施藥作業時，離心式噴頭噴霧系統霧化特性主要受霧化器轉速、風速與施藥流速的影響[25-28]。為解決航空施藥作業時霧滴粒徑變量精細控制的問題，本文進行二次回歸正交試驗[29]，分析風速、施藥流速、霧化器轉速與霧滴粒徑間的相關關系，建立霧滴粒徑模型。試驗中，風速表示施藥時霧化器周圍的氣流絕對速度，直升機施藥作業時飛行速度范圍90～160 km/h，試驗中風速范圍設定為25.46～77.08 m/s，施藥流速表示進入單個霧化器的藥液流速，Aerial-E型電動轉籠霧化器作業時常規流速范圍為7.0～8.0 L/min，試驗中施藥流速范圍設定為5.0～10.0 L/min，霧化器轉速范圍設定為2 000～6 000 r/min，為進行失擬性檢驗，設定零水平試驗次數m0=3，星號臂長度γ=1.353，正交試驗因素編碼如表2。

表2 試驗因素編碼Tab.2 Experiment factor codes

二次回歸正交試驗設計方案與結果如表3所示，Z1、Z2、Z3分別表示風速、施藥流速與霧化器轉速的編碼值，粒徑均值d′為3次重復數據的平均值，每次測量時間50 s，本試驗中以粒徑均值d′作為參照，建立霧滴粒徑模型。

所建立霧滴粒徑模型的三元二次回歸方程為

d=a+b1Z1+b2Z2+b3Z3+b12Z1Z2+b13Z1Z3+b23Z2Z3+b11Z′1+b22Z′2+b33Z′3 (4)

(5)

式中d——模型預測值

a、b1、b2、b3、b12、b13、b23、b11、b22、b33為回歸系數，得各回歸系數依次為254.896、-126.578、-5.041、-48.242、-5.996、38.304、-18.646、49.487、-11.978、-2.975，計算方法見文獻[29]。

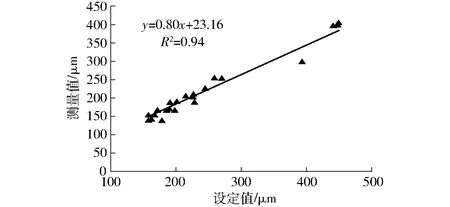
對回歸方程進行方差顯著性分析，得到回歸方程各參數Z1、Z2、Z3、Z1Z2、Z1Z3、Z2Z3、Z′1、Z′2、Z′3的F值為98.853、0.149、13.633、0.144、5.896、1.397、8.246、0.483、0.028，取顯著性水平α=0.05時，F0.05(1，7)=5.59，則本文視F>F0.05(1，7)為高度顯著水平，包括F(Z1)、F(Z3)、F(Z1Z3)與F(Z′1)；F

d=254.896-126.578Z1-48.242Z3+
38.304Z1Z3+49.487Z′1

(6)

2.2 二次殘差補償霧滴粒徑模型優化

2.2.1第1次優化霧滴粒徑模型

在實際試驗過程中，由于霧滴粒徑主要受風速、霧化器轉速與施藥流速的相互影響，且Aerial-E電動轉籠霧化器霧化后的霧滴粒徑受施藥流速的影響較大，如圖5。圖中試驗序號表示不同的試驗條件，序號1表示風速v=70.35 m/s、霧化器轉速n=5 478 r/min，序號2表示風速v=70.35 m/s、霧化器轉速n=2 522 r/min，序號3表示風速v=32.19 m/s、霧化器轉速n=5 478 r/min，序號4表示風速v=32.19 m/s、霧化器轉速n=2 522 r/min。由圖5可知，當風速與霧化器轉速一定時，隨施藥流速的增大，霧滴粒徑變大，但霧滴粒徑與施藥流速間為非線性關系。由式(6)可知，霧滴粒徑受風速與霧化器轉速的相互作用，未考慮施藥流速的影響，因此本文添加補償因子，以得到第1次優化霧滴粒徑補償模型。

圖5 霧滴粒徑與施藥流速關系Fig.5 Relationship between droplet diameter and flow rate

在霧滴粒徑模型顯著性分析中，忽略因素顯著性從高到低依次為F(Z2Z3)、F(Z′2)、F(Z2)、F(Z1Z2)、F(Z′3)，為考慮施藥流速對霧滴粒徑的影響，本文取施藥流速與霧化器轉速的交互作用項Z2Z3作為補償因子，得第1次優化霧滴粒徑補償模型

d=254.896-126.578Z1-48.242Z3+
38.304Z1Z3+49.487Z′1-18.646Z2Z3

(7)

為驗證第1次優化霧滴粒徑補償模型在各個變量范圍內的擬合情況，進行回歸方程的失擬性檢驗，將補償因子列入回歸方程的回歸項，得回歸方程的F檢測值FLf為36.058，取顯著性水平α=0.025時，得F0.025(9，2)=39.390，FLf

對式(7)進行回歸方程回代，得到風速、施藥流速、霧化器轉速與霧滴粒徑間的第1次優化霧滴粒徑補償模型

d=1 117.26-0.13v2-26.00v+28.03q-
0.05n+0.001 4vn-0.007qn

(8)

將第1次優化霧滴粒徑補償模型進行等效變形，得到可根據霧滴粒徑設定值、風速與施藥流速計算霧化器轉速的第1次優化霧滴粒徑補償輸出模型

(9)

2.2.2第2次優化霧滴粒徑模型

試驗發現第1次優化霧滴粒徑補償模型預測值與測量值的殘差較大，其殘差與風速、施藥流速、霧化器轉速間存在非線性關系。鑒于機器學習中的集成模型可以組合多個弱監督模型的優點以得到更好更全面的強監督模型，同時將提升樹學習器(Boosting)與裝袋學習器(Bagging)結合的集成模型可有效提高機器學習效果，減少方差，降低過擬合影響[30-31]。本文采用以數據驅動的機器學習方法，利用提升樹學習器與裝袋學習器結合的集成模型對第1次優化霧滴粒徑補償模型殘差的影響因素進行分析，構建第2次殘差預測模型，并將第2次殘差預測模型與第1次優化霧滴粒徑補償模型線性疊加得到二次殘差補償霧滴粒徑模型。在圖1所示霧化試驗平臺上進行第1次優化霧滴粒徑補償模型驗證試驗，得到400組不同試驗條件下模型預測值與試驗測量值間殘差數據{(v1,q1,n1,ε1),(v2,q2,n2,ε2)，…，(vm,qm,nm,εm)}，εm為第m次驗證試驗殘差，將數據的70%作為訓練模型，30%作為驗證模型，在Matlab的regression learner工具箱下進行數據擬合，選用v、q、n作為自變量，ε作為響應量，利用可視化界面設定模型優化器為貝葉斯優化，迭代數為100，模型調優方法為5折交叉法，以使模型泛化能力最優，調優訓練過程如圖6所示。

圖6 調優訓練曲線Fig.6 Optimization training curves

由圖6可知，最終最小均方誤差趨于穩定，不再波動，模型預測值與實際值接近，其均方根誤差為9.31，均方誤差為86.78，平均絕對誤差為5.83，將第2次殘差預測模型與第1次優化霧滴粒徑補償模型線性疊加，得到二次殘差補償霧滴粒徑模型

d=1 117.26-0.13v2-26.00v+28.03q-0.05n+
0.001 4vn-0.007qn+ε′

(10)

式中ε′——第2次殘差預測模型預測值

將二次殘差補償霧滴粒徑模型進行等效變形，得到電動轉籠二次殘差補償霧化模型

(11)

該模型可根據霧滴粒徑設定值、風速與施藥流速計算得到最終霧化器轉速，以實現對霧滴粒徑的變量精細控制。

本研究采用決定系數(R2)、均方誤差(MSE)、均方根誤差(RMSE)、平均絕對誤差(MAE)4個指標對所建立模型進行評價。

3 模型性能試驗驗證

3.1 模型驗證試驗

為驗證所建立二次殘差補償霧滴粒徑模型的預測精度，在圖1所示試驗平臺上進行模型驗證試驗，設定風速為25.46、33.80、42.62、51.27、51.54、60.68、70.35、77.08 m/s，設定施藥流速為5.0、5.7、6.7、7.5、8.3、9.3、10.0 L/min，設定霧化器轉速為2 000、2 500、3 000、3 500、4 000、4 500、5 000、5 500、6 000 r/min，共進行41組試驗，每組數據測量時間50 s。

試驗結果如表4，其中，1～9組試驗表明，二次殘差補償霧滴粒徑模型預測值與測量值間偏差絕對值最大為10.78%；10～18組試驗表明，風速與施藥流速一定時，霧滴粒徑隨霧化器轉速的升高而減小，霧滴粒徑與霧化器轉速呈負相關，模型預測值與測量值間偏差絕對值最大為10.51%；19～32組試驗表明，霧化器轉速與施藥流速一定時，霧滴粒徑隨風速的升高而降低，霧滴粒徑與風速呈負相關，模型預測值與測量值間偏差絕對值最大為10.70%；33～41組試驗表明，風速與霧化器轉速一定時，霧滴粒徑與施藥流速呈正相關，模型預測值與測量值間偏差絕對值最大為6.75%。綜上所述，二次殘差補償霧滴粒徑模型預測偏差絕對值最大為10.78%。

表4 模型驗證試驗結果Tab.4 Results of model validation experiment

3.2 模型對比試驗

為驗證二次殘差補償霧滴粒徑模型的優勢，在圖1所示試驗平臺上進行試驗，得到200組風速、施藥流速、霧化器轉速與霧滴粒徑測量值的數據，將其作為對比試驗數據集，對比3種模型的預測效果。

3.2.1無補償霧滴粒徑模型

將數據集中的風速、施藥流速與霧化器轉速數據作為輸入量，代入無補償的霧滴粒徑模型中得到霧滴粒徑的模型預測值，模型預測值與試驗測量值的擬合曲線如圖7所示。

圖7 無補償霧滴粒徑模型擬合曲線Fig.7 Fitting curve of non-compensation droplet diameter model

由圖7可知，無補償霧滴粒徑模型預測值與測量值的R2為0.89，其MSE為1 688.77 μm2，RMSE為41.09 μm，MAE為25.14 μm。

3.2.2第1次優化霧滴粒徑補償模型

將數據集中的風速、施藥流速與霧化器轉速數據作為輸入量，代入第1次優化霧滴粒徑補償模型得到霧滴粒徑的模型預測值，模型預測值與試驗測量值的擬合曲線如圖8所示。

圖8 第1次優化霧滴粒徑補償模型擬合曲線Fig.8 Fitting curve of the first optimization droplet diameter compensation model

由圖8可知，第1次優化霧滴粒徑補償模型預測值與測量值的R2為0.90，比無補償霧滴粒徑模型提高0.01，其MSE為1 404.14 μm2，RMSE為37.41 μm，MAE為24.33 μm，均小于無補償霧滴粒徑模型，表明第1次優化霧滴粒徑補償模型預測精度優于無補償霧滴粒徑模型。

3.2.3二次殘差補償霧滴粒徑模型

將數據集中的風速、施藥流速與霧化器轉速數據作為輸入量，代入二次殘差補償霧滴粒徑模型中得到霧滴粒徑的模型預測值，模型預測值與試驗測量值的擬合曲線如圖9所示。

圖9 二次殘差補償霧滴粒徑模型擬合曲線Fig.9 Fitting curve of quadratic residual compensation droplet diameter model

由圖9可知，二次殘差補償霧滴粒徑模型預測值與測量值的R2為0.95，比第1次優化霧滴粒徑補償模型提高0.05，其MSE為582.84 μm2，RMSE為24.14 μm，MAE為14.30 μm。

對比3種模型試驗結果可知，二次殘差補償霧滴粒徑模型的R2最高，MSE、RMSE與MAE均為最小，表明二次殘差補償霧滴粒徑模型可行，該模型預測精度更高，對實現霧滴粒徑可控具有更高的價值。

3.3 系統應用試驗

利用所設計電動轉籠霧化系統進行應用性試驗，在圖1所示霧化試驗平臺進行試驗，設定風速為33.80、51.54、60.68、69.00 m/s，設定施藥流速為5.0、6.7、8.3、10.0 L/min，設定霧滴粒徑為146、155、158、180、215、240、421 μm，3種設定條件隨機組合，以檢測電動轉籠霧化系統霧化效果，即霧滴粒徑與相對分布跨度，共得到40組霧滴粒徑測量值數據。每組數據測量時間50 s。

電動轉籠霧化系統工作時，設定霧滴粒徑后，系統測量風速與施藥流速，并根據電動轉籠二次殘差補償霧化模型計算得到霧化器轉速，以得到理想霧化效果，該系統中霧滴粒徑設定值可等效為對應風速、施藥流速與霧化器轉速條件下的二次殘差補償霧滴粒徑模型預測值，因此本研究將電動轉籠霧化系統的霧化效果與模型的預測效果對比，以驗證電動轉籠霧化系統的霧化效果。

圖10為電動轉籠霧化系統霧滴粒徑設定值與試驗測量值的擬合曲線，該系統霧滴粒徑設定值與測量值的R2為0.94，其MSE為653.39 μm2，RMSE為25.56 μm，MAE為20.34 μm，表明電動轉籠二次殘差補償霧化模型應用到電動轉籠霧化系統時，準確度降低，但該系統的R2、MSE、RMSE、MAE各項指標均優于無補償霧滴粒徑模型與第1次優化霧滴粒徑補償模型的預測效果，表明電動轉籠二次殘差補償霧化模型應用到實踐中時，雖然模型的準確度有所降低，但仍然具有一定的實用性。

圖10 電動轉籠霧化系統霧滴粒徑設定值與測量值擬合曲線Fig.10 Fitting curve between expected and measured droplet diameter of electricity atomization system

電動轉籠二次殘差補償霧化模型實際應用時，準確度降低。分析原因可知，由于所設計電動轉籠霧化系統工作時，設定霧滴粒徑后，系統首先設定殘差為0，并測量風速與施藥流速，計算霧化器轉速，即根據第1次優化霧滴粒徑補償輸出模型計算得到霧化器轉速，然后將計算得到的霧化器轉速與風速、施藥流速作為輸入量，代入第2次殘差預測模型，得到殘差，最后將殘差、風速、施藥流速與霧滴粒徑設定值代入電動轉籠二次殘差補償霧化模型，計算最終霧化器轉速，在計算過程中，由于殘差預測模型輸入量中的霧化器轉速是根據第1次優化霧滴粒徑補償輸出模型計算得到，在迭代運算過程中，造成輸入偏差，導致該系統霧化效果有所降低。

相對分布跨度是衡量霧滴均勻性的指標，其值越大，表明霧化均勻性越差，其值越小，表明霧化均勻性越好；由圖11可知，電動轉籠霧化系統霧化后霧滴相對分布跨度均小于1.6，霧化均勻性較好。

圖11 霧滴相對分布跨度Fig.11 Relative span of droplet

綜上所述，基于電動轉籠二次殘差補償霧化模型的電動轉籠霧化系統在恒定的風速、施藥流速條件下，能自動測量風速與施藥流速，實現霧滴粒徑可控。

4 結論

(1)以Aerial-E型電動轉籠霧化器為控制對象，進行了二次回歸正交試驗，分析了風速、施藥流速、霧化器轉速與霧滴粒徑間的相關關系，建立了霧滴粒徑模型，在補償因子修正關系模型的基礎上，利用機器學習對模型殘差進行了建模，從而實現了模型優化，得到二次殘差補償霧滴粒徑模型。試驗結果表明，二次殘差補償霧滴粒徑模型預測偏差絕對值最大為10.78%，其預測值與測量值的R2為0.95，MSE、RMSE、MAE最小，分別為582.84 μm2、24.14 μm、14.30 μm，說明二次殘差補償霧滴粒徑模型預測結果最優。

(2)搭建了基于電動轉籠二次殘差補償霧化模型的電動轉籠霧化系統，該系統可在恒定風速、施藥流速環境下，實現霧滴粒徑可控，且系統霧滴粒徑設定值與測量值的R2為0.94，霧滴相對分布跨度均小于1.6，可實現在風速、施藥流速穩定情況下的霧滴粒徑可控，霧化均勻性較好。