小學數學幾何概念深度教學“四注重”

吳洵

摘? 要：小學數學幾何概念具有高度的抽象性和概括性。在幾何概念的教學中，教師要力求“有深度”，從學生已有的經驗出發，注重概念的本質教學，幫助學生建立形象感知;注重概念的對比教學，促進對概念的深度理解;注重概念的關聯教學，培養學生思維的整體性;注重概念的應用教學，培養學生思維的深刻性。從而引導學生切實地理解和掌握概念，運用概念分析和解決問題。

關鍵詞：深度教學;概念本質;概念關聯;概念對比;概念應用

數學概念是人類對現實世界空間形式和數量關系的簡明概括，是數學思維的細胞。其中，幾何概念屬于“圖形與幾何”的范疇，是幾何基礎知識的基石，具有高度的抽象性和概括性。深度教學理論認為，學生只有從本質上把握概念的內涵，才能形象感知，深度理解，靈活應用概念，促進其思維的“生長”。而小學生的思維以具體形象思維為主。為此，在進行幾何概念教學時，教師應努力從學生已有認知出發，抓住知識的本質，多維度引導學生深入學習。

一、注重概念的本質，建立形象感知

幾何概念具有較強的抽象性和概括性，而小學中低年級的學生，思維具有形象性，知識經驗不夠豐富，這與前者形成了鮮明的對比。因此，教師在教學幾何概念時，要圍繞概念的本質屬性，從學生已有生活經驗和知識經驗出發，幫助學生形成感性經驗，全面把握概念的內涵，從而培養學生思維的抽象性和概括性。如人教版三年級上冊《周長》一課，其概念是：封閉圖形一周的長度，是它的周長。從字面上看，概念不難理解，學過概念后，學生也能對周長的概念進行判斷和運用。但是，隨著學習的不斷深入，尤其是當學生學習了面積之后，對周長和面積兩個概念總是容易發生混淆。原因在于，很多教師在教學“周長”時，是從字面上的“一周”和“封閉”入手，而非從周長的本質屬性“長度”一詞入手。筆者認為，教學時，教師應牢牢抓住概念的本質屬性，分兩個層次對周長的概念進行詮釋。第一層次，讓學生量一根鐵絲的長度，再把鐵絲變彎，最后頭尾相接圍成一個封閉圖形，再讓學生觀察它的長度，讓學生體會周長首先指的是長度，是一周的長度。第二層次，讓學生用同樣長的線繩圍成形狀不同的封閉圖形，讓學生體會線繩的長度就是封閉圖形的周長。如此教學，強調了周長的本質，讓學生初步建立起對“周長”的形象感知，這有利于避免后續學習“面積”對于“周長”的干擾。

再如，人教版五年級下冊《體積》一課，其概念是：物體所占空間的大小叫作物體的體積。“空間”就是體積概念的本質屬性，學生對“空間”“空間的三維特征”的認識程度，決定了他們對“體積”這一概念認識的深度。但“空間”是“空”的，對學生來說十分抽象，不易理解。教學時，教師應圍繞這一本質屬性，分三個層次進行教學：第一，拿出已經裝了一些東西的杯子讓學生觀察是否還能加水，讓學生看出“空隙”，從而顯性地感知空間的存在;第二，通過動態倒水的過程，讓學生形象地感知剩余空間越來越小的過程，加深對“空間”的體驗;第三，通過摸一摸課桌抽屜空間的長度、寬度、高度，指一指教室空間的長度、寬度、高度，想象公共汽車、整個宇宙的空間等，讓學生多角度地感受到空間有大小以及空間具有長度、寬度、高度這三個維度的特征。這樣教學，就能比較清楚、顯性地讓學生感受到體積概念的本質，由具體到抽象，為學生思維的抽象性和概括性打下基礎，從而培養學生的空間觀念。

二、注重概念的對比，促進深度理解

有對比才有鑒別，通過同類事物的對比，有利于幫助學生發現同類概念的本質特點。在小學數學的幾何概念中，有很多相近的概念，教師在教學同類概念時，要抓住學生容易混淆的“點”，進行對比教學，從而促進學生對概念的深度理解。如人教版三年級下冊《面積》一課，其概念是：物體表面或封閉圖形的大小，就是它們的面積。這一概念包含兩層意思，其一是物體表面的大小;其二是封閉圖形所占面的大小。教師在引導學生理解時，首先應將“平面”與“曲面”進行對比，豐富對“物體表面”的形象感知;其次，還應適時將“封閉圖形”與“平面圖形”進行對比，加深對“封閉”一詞的體悟，強化學生對“面”這一概念的深度理解。此外，在教學過程中經常發現，學生最容易混淆的點在于“面積”與“周長”，為此教師可采取以下策略進行對比：在格子圖中出示一個長方形，首先，讓學生數一數、算一算這個長方形的周長和面積各是多少;其次，引導學生想象、交流將這個長方形一周的長即4條邊展開，會是什么樣;學生反饋后，隨即通過課件演示讓學生直觀感受此長方形4條邊展開后是一條“線段”;引導學生用手勢分別比畫這個長方形的“周長”和“面積”。通過層層對比教學，促進學生對“面積”這一概念的深度理解，同時在對比的感知操作中充分發展了學生的空間觀念。

又如學習人教版五年級下冊《容積》一課后，學生總是會混淆“體積”和“容積”的概念。教師在授課過程中要注重以“容積和體積一樣嗎”為主線，進行對比教學，借助問題思考、物體觀察、空間想象、類比推理等形式，幫助學生感知“有些物體是有體積沒有容積的”“有些物體是既有體積也有容積的”“容積需要從里邊觀察，體積需要從外面觀察”等，讓學生在對比活動中感受二者的區別，從而使思維的認識由“表面”走向“深刻”。

三、注重概念的關聯，培養整體思維

新知識的建構往往依賴于頭腦中已有的知識。小學數學幾何知識的系統性強，前后聯系密切，但由于學生的思維發展水平和接受能力的限制，有些知識是分幾節課或幾個學期進行編排的。因此，對一些有聯系的概念，教師在一定的階段應引導學生進行系統整理，讓學生建立知識網絡，形成良好的認知結構。例如，教學人教版四年級上冊《認識平行四邊形》一課，平行四邊形是在認識長方形、正方形等圖形的知識基礎上學習的。長方形、正方形的知識是學習平行四邊形的上位知識，教師應充分了解學生的知識基礎，從學生的最近發展區出發，設計教學：可以先復習長方形、正方形的特征和探究方法，回憶、建立起表象，進而讓學生通過猜想、操作、驗證等方法抽象出平行四邊形的特征;然后引導學生通過比較、觀察、動手操作等方法，嘗試探索這三種圖形之間的關系，明確異同點，進而把分散的圖形進行關聯，整體建構，讓學生經歷從部分到整體的過程體驗，從而豐富概念的外延，培養學生思維的整體性。

又如教學《容積》一課時，教師除了幫助學生厘清“容積”和“體積”的概念，還需要明確容積與體積是緊密聯系的，在空間與體積等上位知識的基礎上，需將二者進行關聯，讓學生清晰地認識到“體積”和“容積”二者凸顯的內涵都是指空間的大小，將“體積”與“容積”這兩個概念納入“空間”這一體系中，讓學生比較深刻、全面地掌握概念。

四、注重概念的應用，培養深刻思維

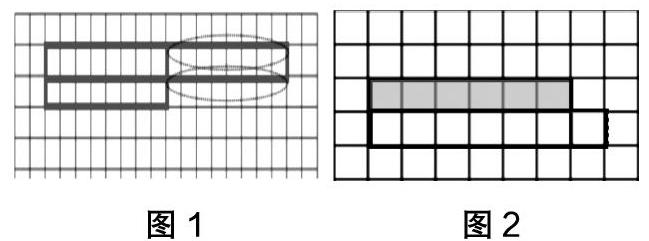
概念學習的最高層次是概念的應用。通過應用已有概念解決相關問題，可以讓學生將某一個或一些概念依據問題情境所提供的信息進行重現、提煉、概括，并使它們相互作用，融會貫通。如人教版三年級下冊《面積》單元的練習第75頁中出現了“探究長方形面積和周長的關系”的習題。此題的設計，一方面旨在讓學生根據面積或周長確定長和寬，培養逆向思維;另一方面是引導學生發現面積和周長之間的關系。教學時，教師不能草草評講，而是要深挖知識進行教學，以培養學生思維的深刻性。教師可出示問題“在方格紙上，畫出面積是16平方厘米的長方形，你能畫幾個？”引導學生分別畫出長方形并計算出這些長方形的周長，充分利用圖形（圖1）引導學生發現規律：從長是16cm，寬是1cm的長方形變成長是8cm，寬2cm的長方形后，雖然寬多了2cm，但長少了2個8cm即16cm，所以周長比原來少了14cm，通過觀察、對比，再次厘清了周長概念的本質。以此類推，引導學生充分地從數據的變化和圖形的變化中發現規律：“當面積相等時，長方形的長和寬越接近，周長越小。”

當學生深刻體悟到該規律后，可引發以下問題：“周長相等的長方形，長和寬越接近，面積會怎么變化？”對此，教師可抓住契機，繼續引導學生深入思考：“周長是16cm的長方形，你能畫出幾個？”當學生匯報后，教師及時在白板中畫出相應的圖形，同樣引導學生深入研究圖形（圖2），從長是7cm，寬是1cm的長方形變成長是6cm，寬2cm的長方形后，長少了1cm，面積少了1cm2，但同時寬多了1cm，面積增加了6cm2，所以面積比原來增加了5cm2……學生最終得出結論：“當長方形的周長相等時，長和寬越接近，面積越大。”進而用此結論解決：“不計算，判斷12×23和13×22的大小。”通過習題的應用，“以形助數”“以數輔形”，豐富對這兩個規律的理解。這樣教學，讓學生經歷了應用概念本質屬性解決問題的過程，鞏固、完善、拓展了概念，培養了學生思維的深刻性。

綜上所述，教師在教學幾何概念時，要充分挖掘概念的本質，多層次引導學生建構概念、對比概念、關聯概念、應用概念，讓學生在觀察、操作、體驗、實踐中感悟概念的內涵與本質，促進學生思維的發展和空間觀念的形成。