基于主要問題，關(guān)注學(xué)習(xí)能力

丁寧 劉賢虎

摘? 要：傳統(tǒng)教學(xué)只有教師知道去哪里以及如何去那里，將知識(shí)咀嚼碎了喂給學(xué)生，學(xué)生只是被動(dòng)接受，沒有學(xué)會(huì)主動(dòng)學(xué)習(xí)。《不規(guī)則物體的體積》將主要問題集中呈現(xiàn)，明確學(xué)習(xí)要點(diǎn)，給足時(shí)間讓學(xué)生進(jìn)行自主、探究、協(xié)作的主動(dòng)學(xué)習(xí)。在這一過程中，學(xué)生知道去哪里和如何去，從學(xué)會(huì)走向會(huì)學(xué)，真正促進(jìn)學(xué)習(xí)能力的提升。

關(guān)鍵詞：?jiǎn)栴};引發(fā);探究;建模;問題解決

一、教學(xué)內(nèi)容

人教版數(shù)學(xué)五年級(jí)下冊(cè)第39頁(yè)例6及練習(xí)。

二、教學(xué)目標(biāo)

（1）讓學(xué)生通過操作探究，明確不規(guī)則的物體可以轉(zhuǎn)化成規(guī)則的物體，會(huì)用排水法等求不規(guī)則物體的體積。

（2）經(jīng)歷觀察、實(shí)驗(yàn)、想象、推理等數(shù)學(xué)活動(dòng)過程，歸納概括求不規(guī)則物體體積的方法，滲透轉(zhuǎn)化的數(shù)學(xué)思想，培養(yǎng)學(xué)生解決實(shí)際問題的能力。

（3）體驗(yàn)數(shù)學(xué)與生活的聯(lián)系，激發(fā)學(xué)生的學(xué)習(xí)興趣，培養(yǎng)學(xué)生的推理能力和空間想象能力。

三、教學(xué)過程

1. 問題引發(fā)

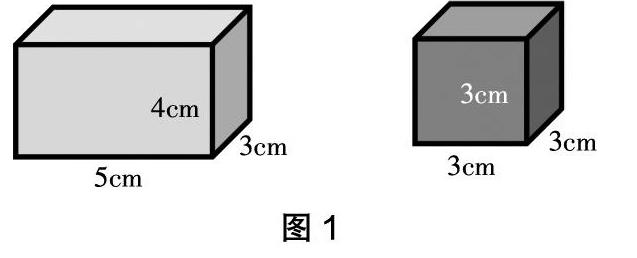
師：孩子們，我們學(xué)習(xí)過長(zhǎng)方體和正方體的體積，來看看，會(huì)求嗎？

生1：這個(gè)長(zhǎng)方體可以用“長(zhǎng)×寬×高”來求，用5×4×3就可以求出這個(gè)長(zhǎng)方體的體積。

生2：正方體可以用“棱長(zhǎng)×棱長(zhǎng)×棱長(zhǎng)”來求，也就是3×3×3=27（cm3）。

師：我們學(xué)會(huì)了如何求長(zhǎng)方體和正方體的體積，但是在我們生活當(dāng)中有很多的物體既不是長(zhǎng)方體的也不是正方體的，比如說老師手上的這塊軟陶，能用這樣的方法直接求出它們的體積嗎？

生：不能。

師：因?yàn)椤?/p>

生：它是不規(guī)則的。

師：是啊，像這樣不規(guī)則的物體在生活中還有很多，比如軟陶、蘋果，等等，它們的體積怎樣來求呢？這節(jié)課我們就來研究這個(gè)問題。（板書課題）

評(píng)析：?jiǎn)栴}引發(fā)立意要高，難度要低，指向要明。由規(guī)則物體的體積引入，到求不規(guī)則物體的體積，從認(rèn)知角度是順應(yīng)，立意高;計(jì)算規(guī)則物體的體積，對(duì)于學(xué)生來說容易，難度低;不規(guī)則物體的體積不能用長(zhǎng)方體、正方體的體積公式來直接計(jì)算，產(chǎn)生學(xué)習(xí)的需求，指向明確。這一環(huán)節(jié)讓學(xué)生知道去哪里，明確學(xué)習(xí)目標(biāo)。

2. 問題探究

師：孩子們，想一想，在生活中還見過哪些不規(guī)則的物體？

生：類似于筆袋也是不規(guī)則的物體。

生：橡皮泥。

生：飛機(jī)。

……

師：其實(shí)在咱們的生活中有很多物體都是不規(guī)則的，老師也找到一些，認(rèn)識(shí)嗎？

師：你想選擇哪一樣來研究？說說你的想法。

生1：我想選擇橡皮泥，因?yàn)樗梢阅蟪晌覀儗W(xué)過的圖形來求。

生2：我選擇土豆，因?yàn)樗梢杂玫肚谐砷L(zhǎng)方體或正方體。

生3：我不同意他的說法，因?yàn)槿绻淹炼骨谐砷L(zhǎng)方體或正方體的時(shí)候，它就少去了一部分，而且土豆就不能保存了。

師：還有像橡皮泥和軟陶一樣可以捏成長(zhǎng)方體或正方體的物體嗎？

生：沒有了。

師：就像大家說的，咱們把橡皮泥、軟陶這樣可以自身改變形狀的物體稱為自身可塑物體，像土豆、石頭這些物體稱為自身不可塑物體。

師：自身可塑物體，它們的體積怎么求呢？自身不可塑物體，它們的體積又怎么求呢？是我講給大家聽聽，還是你們自己去發(fā)現(xiàn)？

生（齊）：自己去發(fā)現(xiàn)。

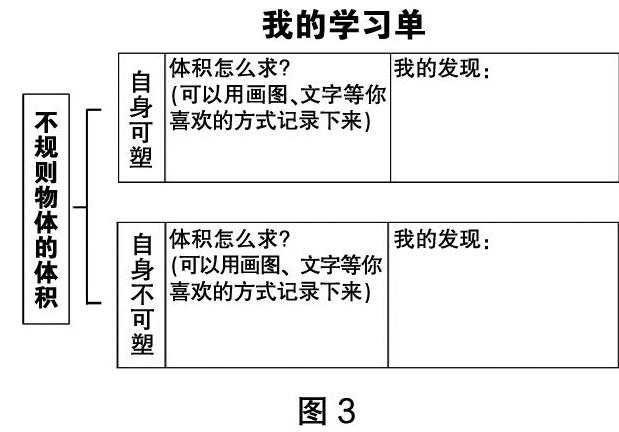
師：老師這里給大家準(zhǔn)備了一些物體和材料，等一下，咱們每個(gè)小組就可以在自身可塑物體中選擇一樣，再?gòu)淖陨聿豢伤芪矬w中選擇一樣來研究，看看大家在研究的過程中有什么發(fā)現(xiàn)？并把你的發(fā)現(xiàn)寫在學(xué)習(xí)單上。

師：自己先想一想選什么，然后再和同伴商量商量，商量好了就可以過來去取了。

學(xué)生自主探究。

評(píng)析：學(xué)生探究首先是建立在獨(dú)立學(xué)習(xí)基礎(chǔ)上的，可以獨(dú)立思考，可以動(dòng)手操作，也可以看書。其次是協(xié)同學(xué)習(xí)，倡導(dǎo)同桌之間的協(xié)同，遇到困難可以求助他人、課本，學(xué)有余力的學(xué)生可以施助他人。這個(gè)環(huán)節(jié)要有足夠的時(shí)間，在10分鐘左右，讓學(xué)生有充分的時(shí)間去親身經(jīng)歷動(dòng)眼觀察、動(dòng)手操作、動(dòng)口表達(dá)、動(dòng)腦思考以及親自探索，如比較、歸納、猜測(cè)、驗(yàn)證、概括等，不能是淺嘗輒止，只有在這樣的學(xué)習(xí)中學(xué)生才能學(xué)會(huì)學(xué)習(xí)。

3. 互動(dòng)建模

師：哪個(gè)小組想和大家分享一下？

生：我們來和大家分享自身不可塑的物體，我們選擇的是土豆，驗(yàn)證方法就是先找來500ml的水，然后把土豆放進(jìn)水里，那么現(xiàn)在500ml的水就升到了600ml，然后我們?cè)侔熏F(xiàn)在的600ml水減去原來的500ml水，得到多余的100ml水，把100ml水轉(zhuǎn)化為100cm3，所以我們得出土豆的體積就是100cm3。

生（齊）：同意。

師：我們明明求的是土豆的體積，你怎么說的卻是水的體積呀？

生：因?yàn)橥炼顾瓉硎遣灰?guī)則物體，而我們不能知道它的長(zhǎng)、寬、高，那么可以通過水，就是排水法來測(cè)量出土豆的體積。這樣就把土豆的體積變?yōu)樗捏w積了。

師：也就是土豆的體積到底等于什么呀？

生：土豆的體積就是等于水多出來的100ml，再把單位轉(zhuǎn)換一下，那100ml就等于100cm3，就是土豆的體積。

師：水怎么會(huì)多呢？

生：因?yàn)橥炼顾臼钦伎臻g的，當(dāng)把它放進(jìn)水里的時(shí)候，土豆就會(huì)把水?dāng)D上去，擠上去的水就是土豆占的空間。

師：實(shí)際上他說的土豆的體積，也就是等于上升的部分水的體積。他提到了排水法，用排水法把求土豆的體積轉(zhuǎn)化成了求——

生：上升部分水的體積。

師：其他小組，你們?cè)谘芯孔陨聿豢伤芪矬w的體積時(shí)，也用到這種辦法了嗎？說說看。

生：我們選擇的是石頭，我們把石頭放進(jìn)500ml的水中，發(fā)現(xiàn)水上升了350ml，這350ml也就等于石頭的體積。把求石頭的體積轉(zhuǎn)化成求上升水的體積。

師：還有研究其他物體的嗎？

生：我們組研究的是雞蛋，我們把雞蛋放進(jìn)500ml的水里，發(fā)現(xiàn)水上升了50ml，我們求出來雞蛋的體積就是50ml，用排水法把雞蛋的體積轉(zhuǎn)化成了上升部分水的體積。

生：我不同意他的說法，毫升是液體的體積單位。雞蛋的體積是50cm3。

師：那他們組求的雞蛋的體積——

生：也是轉(zhuǎn)化成了上升部分水的體積。

師：想一想，咱們用排水法求自身不可塑物體體積的時(shí)候需要記錄哪些數(shù)據(jù)呢？

生：我覺得要記錄原來水的體積和把物體放進(jìn)去之后的體積。

師：自身不可塑的物體我們有辦法求出它們的體積了，那么自身可塑的呢？

生1：我們可以先把一個(gè)不規(guī)則的橡皮泥捏成一個(gè)規(guī)則的長(zhǎng)方體，然后再用尺子去量，量出它的長(zhǎng)、寬、高，就可以計(jì)算出它的體積了。

生2：我想補(bǔ)充，我們也可以捏成一個(gè)正方體，按照正方體的體積公式也可以求出它的體積。

師：聽你們這么一說，橡皮泥的體積就——

生1：等于長(zhǎng)方體或正方體的體積了。

生2：橡皮泥的體積就轉(zhuǎn)化成了長(zhǎng)方體的體積。

師：軟陶呢？

生：也可以轉(zhuǎn)化成長(zhǎng)方體或正方體的體積。

師：同學(xué)們，無論是自身可塑的物體，還是自身不可塑的物體，都能用自己的方法求出它們的體積，可是在大家探究的過程中，有一個(gè)小組選擇了這樣一個(gè)塑料的物體，后來又去換了一個(gè)土豆，你知道為什么嗎？

生：因?yàn)檫@個(gè)物體可能會(huì)浮起來，不會(huì)沉到水里，那就無法用排水法得到它的體積了。

師：在我們生活當(dāng)中還有很多這樣的物體，比如說木頭、塑料、冰糖都不能用排水法求出它們的體積，那么這樣的物體，它們的體積怎樣來求呢？是的，也可以用排沙法、排米法來求，這樣它們的體積就轉(zhuǎn)化成了上升部分沙子、米的體積。

師：無論是自身可塑物體、自身不可塑物體，還是特殊物體都能用這種轉(zhuǎn)化的辦法求出它們的體積，也就是把這些不規(guī)則的物體的體積轉(zhuǎn)化成規(guī)則的、我們學(xué)過的或者可以測(cè)量的物體的體積。這種轉(zhuǎn)化的辦法，在我們之前的學(xué)習(xí)中也有用到過，知道在哪里用到過嗎？

生：我們以前學(xué)過的小數(shù)除法就是轉(zhuǎn)化成整數(shù)除法來計(jì)算的。

生：我們計(jì)算平行四邊形的面積也是轉(zhuǎn)化成我們學(xué)過圖形的面積來求的。

師：是的，在我們上學(xué)期的學(xué)習(xí)中就有用到轉(zhuǎn)化的辦法。在今后學(xué)習(xí)中我們也會(huì)用到這樣的辦法。轉(zhuǎn)化思想是數(shù)學(xué)學(xué)習(xí)中常用的思想方法，其實(shí)學(xué)習(xí)數(shù)學(xué)的過程就是不斷轉(zhuǎn)化的過程，不斷地將未知的問題轉(zhuǎn)化成已知問題的過程，學(xué)會(huì)用轉(zhuǎn)化的策略解決數(shù)學(xué)問題對(duì)咱們今后的學(xué)習(xí)尤為重要。

評(píng)析：學(xué)生經(jīng)歷充分的自主探究與協(xié)同學(xué)習(xí)后，有了較為深刻的認(rèn)識(shí)，通過生生、師生互動(dòng)交流，逐步建立求不規(guī)則物體體積的數(shù)學(xué)模型：不規(guī)則物體轉(zhuǎn)化為規(guī)則物體。在這節(jié)課，學(xué)生從不規(guī)則物體中可塑和不可塑兩類的探究，發(fā)現(xiàn)、總結(jié)解決這一類問題的方法——轉(zhuǎn)化。

4. 問題解決

（1）珊瑚石的體積是多少？

生1：我來說我的方法，沒有放珊瑚，水深6cm，放珊瑚后水深7cm，水上升了1cm，所以珊瑚石的體積就等于8×8×1=64（cm3）。

生2：我的方法是先求出水的體積8×8×6，再求出放進(jìn)珊瑚石后的體積8×8×7，再減去第一次求出的水的體積。

師：對(duì)于這兩種方法，你有什么看法？

生1：我喜歡第一種方法，因?yàn)樗苯佑?jì)算上升部分水的體積，也就是珊瑚石的體積，計(jì)算很簡(jiǎn)便。

生2：我喜歡第二種方法，雖然計(jì)算步驟多一些，但是這種方法一想就明白。

（2）爸爸在一個(gè)底面積為51dm2的長(zhǎng)方體魚缸里放了一個(gè)假山石，水面上升了3cm。這個(gè)假山石的體積有多大？

生1：首先我們要換算單位51dm2=5100cm2，之后再用公式V=Sh=5100×3=15300（cm3）。

生2：我還有一種方法，把3cm換算成0.3dm，所以V=Sh=51×0.3=15.3（dm3）。

師：那這里假山石的體積就轉(zhuǎn)化成了——

生：上升部分水的體積。

師：孩子們，這節(jié)課就要結(jié)束了。想一想，這節(jié)課我們解決了什么問題？遇到了什么困難？你有哪些收獲？

生1：我知道了怎么計(jì)算自身不可塑物體的體積。

生2：這節(jié)課我學(xué)會(huì)了轉(zhuǎn)化的思想，還有排水法。

生3：還學(xué)會(huì)了如何求自身可塑物體的體積。

生4：我還知道了自身可塑物體捏成規(guī)則物體，它的體積不變。

生5：我還知道了轉(zhuǎn)化是多么重要。

生6：我要補(bǔ)充，一開始我寫第8題沒看到單位要換算，經(jīng)過老師提醒才知道，所以我們以后要認(rèn)真審題，看清單位。

師：是啊，要認(rèn)真審題。其實(shí)學(xué)習(xí)就是這樣一個(gè)過程，有時(shí)候想著想著、說著說著就會(huì)了。好了，這節(jié)課我們就上到這里，下課！

評(píng)析：?jiǎn)栴}解決環(huán)節(jié)就是應(yīng)用數(shù)學(xué)模型來解決數(shù)學(xué)問題或生活問題。在這一過程中，培養(yǎng)學(xué)生的遷移與應(yīng)用能力。顯然，需要繼續(xù)繼承和發(fā)揚(yáng)傳統(tǒng)教學(xué)中的優(yōu)勢(shì)，注重問題的層次性、綜合性，也要關(guān)注變式問題的解決。不能讓學(xué)生停留在“對(duì)答案、說解答過程”的低層次思維上，而應(yīng)讓學(xué)生說說“你是怎么想的？”“你認(rèn)為這種想法對(duì)嗎，為什么？” “對(duì)于這種方法，你有什么看法？”等等，發(fā)展學(xué)生的“分析、評(píng)價(jià)、創(chuàng)新”高階思維。

四、全課評(píng)析

在傳統(tǒng)教學(xué)中，存在以下問題：學(xué)生不知道去哪里，更不知道怎么去那里。只有教師知道去哪里以及怎么去，學(xué)生只能被動(dòng)跟隨。教師總是習(xí)慣將知識(shí)咀嚼碎了喂給學(xué)生，導(dǎo)致學(xué)生缺乏獨(dú)立學(xué)習(xí)的能力。一旦離開教師的幫助，學(xué)生就不會(huì)學(xué)習(xí)。針對(duì)以上問題，我們對(duì)傳統(tǒng)課堂教學(xué)進(jìn)行變革，實(shí)施問題教學(xué)，讓學(xué)生從學(xué)會(huì)走向會(huì)學(xué)。問題教學(xué)的流程框架是：?jiǎn)栴}引發(fā)——問題探究——互動(dòng)建模——問題解決。其核心是“問題探究”。一節(jié)課圍繞2、3個(gè)主要問題進(jìn)行探究，問題之間呈現(xiàn)進(jìn)階或并列關(guān)系，并且每個(gè)問題都讓學(xué)生明確學(xué)習(xí)要點(diǎn)，比如畫一畫、寫一寫、看一看、說一說等，其目的就是讓學(xué)生知道去哪里以及如何去。

1. 讓自主、協(xié)作、探究真正發(fā)生

在傳統(tǒng)的課堂，學(xué)生獨(dú)立學(xué)習(xí)的時(shí)間少，而且支離破碎，無法實(shí)現(xiàn)真正的自主、協(xié)作、探究。問題教學(xué)以問題引領(lǐng)促進(jìn)學(xué)生的知識(shí)建構(gòu)和問題解決，將本節(jié)課的核心問題用問題鏈的形式呈現(xiàn)，同時(shí)通過交流互動(dòng)確定問題鏈解決的方法策略，提煉出要點(diǎn)，以學(xué)習(xí)單的形式放手讓學(xué)生去探究。學(xué)生明確自己的學(xué)習(xí)目標(biāo)，也清楚達(dá)成目標(biāo)的途徑方法，并且有較為充足的時(shí)間去獨(dú)立思考、自主探究，同時(shí)倡導(dǎo)同桌、小組間的協(xié)作學(xué)習(xí)，讓求助、施助隨時(shí)發(fā)生。在解決問題鏈的過程中，不斷將學(xué)生的思維引向深入。

2. 讓思考、質(zhì)疑、評(píng)價(jià)成為習(xí)慣

學(xué)習(xí)絕不是被動(dòng)接受的過程，它應(yīng)當(dāng)成為主動(dòng)思考、多元表達(dá)、相互促進(jìn)的過程。教師要?jiǎng)?chuàng)設(shè)激發(fā)學(xué)生主動(dòng)思考的問題情境，可以是生活情境，也可以是數(shù)學(xué)問題情境。學(xué)生有了自己的思考，就可以表達(dá)觀點(diǎn)，進(jìn)行分享、交流。在互動(dòng)交流時(shí)，教師要將質(zhì)疑、評(píng)價(jià)的主動(dòng)權(quán)還給學(xué)生。對(duì)于學(xué)生的觀點(diǎn)，讓學(xué)生去質(zhì)疑對(duì)與錯(cuò)，去評(píng)價(jià)合理與不合理，促進(jìn)學(xué)生高階思維的發(fā)展。

通過問題教學(xué)，教師將以往零碎的問題變?yōu)榻Y(jié)構(gòu)化的思維性問題和知識(shí)性問題，指向數(shù)學(xué)知識(shí)的本質(zhì)和核心。學(xué)生從碎片化的學(xué)習(xí)和思考走向整體的知識(shí)建構(gòu)，實(shí)現(xiàn)從被動(dòng)學(xué)習(xí)變?yōu)橹鲃?dòng)學(xué)習(xí)，從低階思維走向高階思維，促進(jìn)學(xué)生學(xué)習(xí)能力的提升，從學(xué)會(huì)走向會(huì)學(xué)。