研究高考試題的視角與案例

嚴豪東　劉成龍　鐘夢圓

[摘? 要] 文章提出了研究高考試題的八個視角：試題評析、分布、立意、背景、解法、變式、推廣和優化，并以2019年高考數學全國卷Ⅰ理科試題為例進行了說明.

[關鍵詞] 高考試題;視角;案例

高考涉及千家萬戶的利益和萬千學子的夢想. 因此，高考一直是人們討論的熱門話題. 如何應對高考是一線教師關注和思考的焦點問題. 為解決這一問題，首要任務是認識到試題是選拔學生的載體，是構成高考試卷的單元. 于是，對高考的研究要轉移到研究試題上來.[1]如何研究試題呢？首先應明確研究的視角. 在結合高考命題實際、綜合研究因素的情形下，結合具體案例，我們提出了研究試題的8個視角：試題評析、分布、立意、背景、解法、變式、推廣和優化.文中以2019年高考數學全國卷Ⅰ（下文簡稱全國卷Ⅰ）理科試卷為例進行說明.

試題評析

試題評析即試題評價與分析.對試題評析有利于整體把握高考命題動態、感受高考命題原則，領會高考命題精神. 全國卷Ⅰ理科試卷嚴格按照《考試說明》以及《課程標準》命制，繼續貫徹“有利于高校選拔人才、有利于中學素質教育”的指導思想[2]，始終堅持穩中求變、穩中創新、立足基礎、突出能力、滲透文化、考查素養的命題原則. 具體來講，第10、11題以三角函數、圓錐曲線、向量為載體，考查問題解決的通法通解;第12、16題著重考查邏輯推理、閱讀等數學能力;第18題解答入口寬，考查學生的空間想象與數學運算核心素養;等等. 通過分析，不難領悟全國卷Ⅰ所傳達的明確信號：重視教材、扎實基礎、關注通法、注重能力、落實素養和發展創新意識.

試題分布

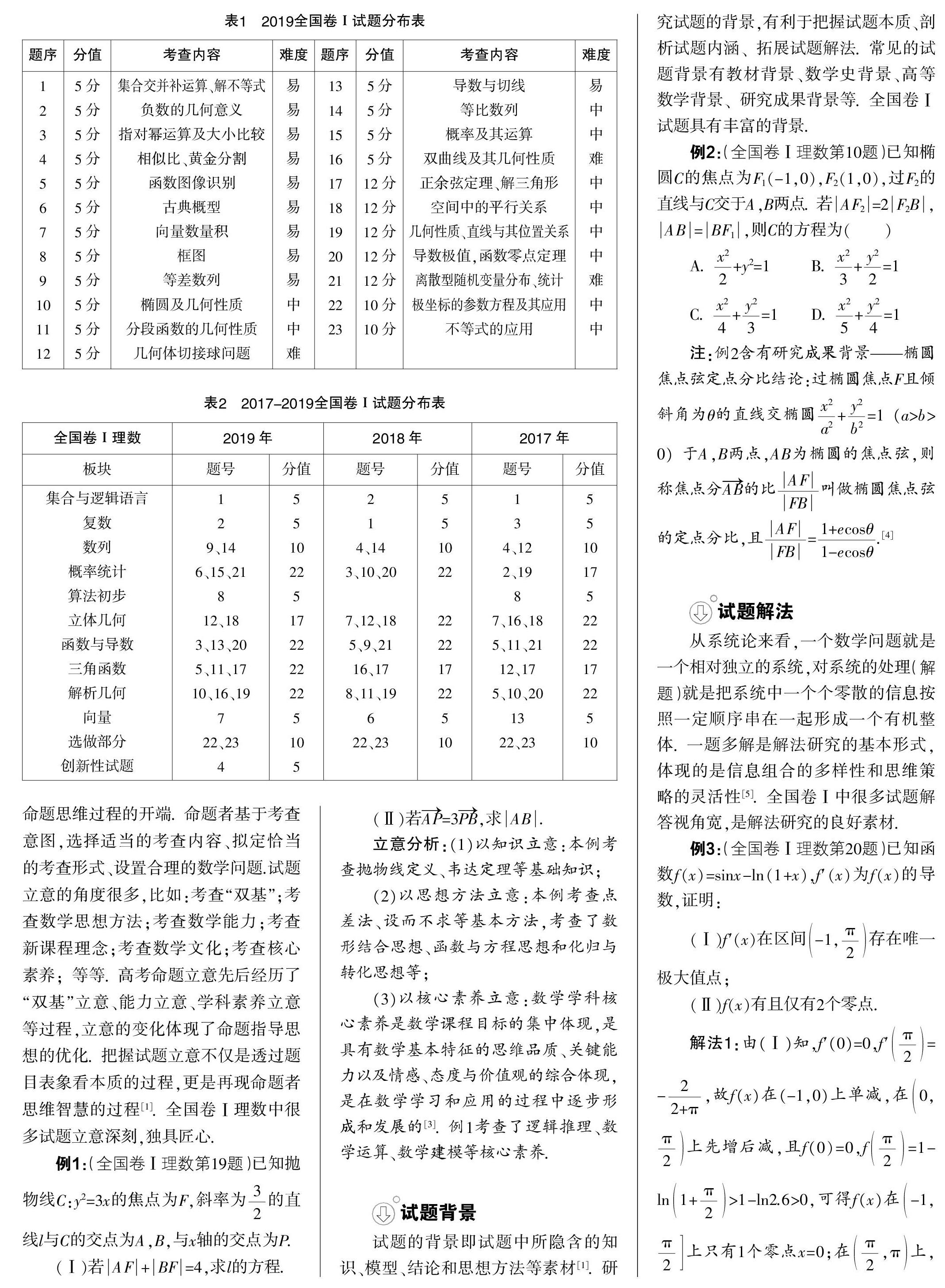
試題分布即試題的分配與布局.包括內容、分值、難度等的分配與布局.研究試題的分布有利于認識試題考什么、怎么考、考到什么程度. 對試題分布的研究需要結合題序、分值、內容、難度這四個要素展開. 下面先給出2019年全國卷Ⅰ試題分析，再結合2017、2018年全國卷Ⅰ分析試題分布.

1. 試題分布（見表1、表2）

2. 信息分析

比較2017、2018年試題，2019年試題在題型、題量上保持不變，但考點與考查形式略有改動，難度要求上有所變化.

（1）復數、集合、數列、向量板塊考查難度不變，分值占比不變.

（2）概率統計、函數與導數、解析幾何占全卷分值比不變，難度有變化.具體來講，解析幾何解答題仍在19題呈現，中等難度，但由兩道較易選擇題減為一道，增加了一道填空壓軸題，總體難度上升;函數與導數板塊，仍有兩道較易選擇題，解答題部分由壓軸題變為中難度試題，總體難度下降;概率與統計板塊由兩道較易選擇題降為一道，增加一道中難度填空題，解答題上升為壓軸題，難度總體上升.

（3）立體幾何與三角函數板塊全卷分值占比對調，難度基本不變.

（4）出現創新應用性試題.

試題立意

試題立意即試題的主題思想. 試題立意是命題者命題意圖的集中體現，是命題思維過程的開端.命題者基于考查意圖，選擇適當的考查內容、擬定恰當的考查形式、設置合理的數學問題.試題立意的角度很多，比如：考查“雙基”;考查數學思想方法;考查數學能力;考查新課程理念;考查數學文化;考查核心素養;等等. 高考命題立意先后經歷了“雙基”立意、能力立意、學科素養立意等過程，立意的變化體現了命題指導思想的優化.把握試題立意不僅是透過題目表象看本質的過程，更是再現命題者思維智慧的過程[1]. 全國卷Ⅰ理數中很多試題立意深刻，獨具匠心.

例1：（全國卷Ⅰ理數第19題）已知拋物線C：y2=3x的焦點為F，斜率為的直線l與C的交點為A，B，與x軸的交點為P.

（Ⅰ）若AF+BF=4，求l的方程.

（Ⅱ）若=3，求AB.

立意分析：（1）以知識立意：本例考查拋物線定義、韋達定理等基礎知識;

（2）以思想方法立意：本例考查點差法、設而不求等基本方法，考查了數形結合思想、函數與方程思想和化歸與轉化思想等;

（3）以核心素養立意：數學學科核心素養是數學課程目標的集中體現，是具有數學基本特征的思維品質、關鍵能力以及情感、態度與價值觀的綜合體現，是在數學學習和應用的過程中逐步形成和發展的[3]. 例1考查了邏輯推理、數學運算、數學建模等核心素養.

試題背景

試題的背景即試題中所隱含的知識、模型、結論和思想方法等素材[1]. 研究試題的背景，有利于把握試題本質、剖析試題內涵、拓展試題解法. 常見的試題背景有教材背景、數學史背景、高等數學背景、研究成果背景等. 全國卷Ⅰ試題具有豐富的背景.

例2：（全國卷Ⅰ理數第10題）已知橢圓C的焦點為F1（-1，0），F2（1，0），過F2的直線與C交于A，B兩點. 若AF2=2F2B，AB=BF1，則C的方程為（? ）

A. +y2=1 B. +=1

C. +=1 D. +=1

注：例2含有研究成果背景——橢圓焦點弦定點分比結論：過橢圓焦點F且傾斜角為θ的直線交橢圓+=1（a>b>0）于A，B兩點，AB為橢圓的焦點弦，則稱焦點分的比叫做橢圓焦點弦的定點分比，且=.[4]

試題解法

從系統論來看，一個數學問題就是一個相對獨立的系統，對系統的處理（解題）就是把系統中一個個零散的信息按照一定順序串在一起形成一個有機整體. 一題多解是解法研究的基本形式，體現的是信息組合的多樣性和思維策略的靈活性[5]. 全國卷Ⅰ中很多試題解答視角寬，是解法研究的良好素材.

試題變式

變式是指相對于某種范式，不斷變更問題情境或改變思維角度，使事物的非本質屬性時隱時現，而事物的本質屬性保持不變的變化方式. 變式能有效控制題海戰術，幫助學生形成良好的認知結構.

例5：（2019全國卷Ⅰ理數第16題）雙曲線-=1的左、右焦點分別為F1，F2，過F1的直線與雙曲線的兩條漸近線分別交于A，B兩點. 若=，·=0，則C的離心率為__________.

視角1：變試題求解目標

變式1：雙曲線-=1的左、右焦點分別為F1，F2，過F1（-1，0）的直線與雙曲線的兩條漸近線分別交于A，B兩點.若=，·=0，則雙曲線方程為__________.

視角2：變試題條件

變式2：雙曲線-=1的左、右焦點分別為F1，F2，坐標原點為O，過F1的直線與雙曲線的兩條漸近線分別交于A，B兩點. 若=，OA∥F2B，則C的離心率為__________.

視角3：變試題背景及條件

變式3：橢圓+=1的左、右焦點分別為F1，F2，過左焦點F1的直線l1與過右焦點F2的直線l2交于B點. A為l1上的一點，若=，·=0，F1F2=2F2B，則C的離心率為__________.

視角4：變試題內涵及條件

變式4：雙曲線-=1的左、右焦點分別為F1，F2，過左焦點F1的直線l1與雙曲線兩支分別交于A，B兩點. 若3=，·=0，則C的離心率為__________.

試題優化

試題命制是一個嚴肅而充滿創造的系統工程. 命題既要關注知識、能力、素養的考查，又要注重合適的難度、有效的信度和適當的區分度的設置，更要關注試題的嚴謹性. 嚴謹性是數學的基本特征，它要求數學試題內容科學、表述準確、條件相容、問題明確等等[6]. 盡管高考試題經過無數次打磨，但遺憾的是個別高考試題存在瑕疵. 面對這些瑕疵，我們在包容的同時，更應具有反思的行動和優化的策略，以此督促命題工作的完善.

例6：（2019全國卷Ⅰ理數第4題）古希臘時期，人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是（≈0.618，稱為黃金分割比例），著名的“斷臂維納斯”便是如此.此外，最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也為黃金分割比. 若某人滿足上述兩個黃金分割比，且腿長為105cm，頭頂至脖子下端的長度為26cm，則其身高可能是（? ）

A. 165cm B. 175cm

C. 185cm D. 190cm

此題存在著命題內容上的缺陷，便于說明，這里先看一個網紅解法：

首先，維納斯是女性，排除C，D;其次，東方女性理想身高是165，西方女性是175，維納斯是外國人，排除A，選B.

網紅解法從常識的角度得到了試題正確的答案. 歪打正著背后，實質上是命題上的重大失誤所致. 華南師大何小亞教授指出：“由于此題存在著命題內容上的缺陷，加上26、105、165、175、185、 190這幾個關鍵數據設置技術的不到位，此題很難考出命題者想考的東西.”因此，我們有必要對試題進行優化：將選項改為：

A. 171cmB. 173cm

C. 175cmD. 178cm

評注：數學是講理的.數據優化后可以很好地考查學生的運算素養、模型素養、推理能力和數據分析能力，能有效抑制歪打正著.

參考文獻：

[1]? 劉成龍，余小芬. 研究高考試題的視角與案例[M]. 成都：四川大學出版社，2018.

[2]? 朱恒元. 聚焦核心素養 打造優質課堂——2018年全國各地高考數學試卷的特點及啟示[J]. 中國數學教育，2018（Z4）.

[3]? 中華人民共和國教育部. 普通高中數學課程標準（2017年版）[M]. 北京：人民教育出版社，2017.

[4]? 顧日新. 圓錐曲線焦點分弦的一個統一結論[J]. 中學數學研究，2009（09）.

[5]? 鄭云升，向婉詩，劉成龍. 《怎樣解題表》指導下的解題實踐——以2012年成都中考第24題為例[J].數學教學通訊，2017（05）.

[6]? 鐘夢圓，劉成龍，董萬平. 一道條件相互矛盾的中考試題[J]. 中學數學，2019（18）.