磁懸浮控制力矩陀螺高速轉子的高精度位置控制

湯繼強，崔 旭，袁新竹，隗同坤

(1. 北京航空航天大學 儀器科學與光電工程學院，北京 100191；2. 北京航空航天大學 新型慣性儀表與導航系統(tǒng)技術國防重點學科實驗室，北京 100191)

1 引 言

控制力矩陀螺(Control Moment Gyroscope，CMG)是一種通過改變角動量方向來調整航天器姿態(tài)和抑制干擾的姿控執(zhí)行機構[1]，主要由高速轉子系統(tǒng)和框架伺服系統(tǒng)組成[2]。根據所采用軸承的支承類型，可以被分為機械控制力矩陀螺和磁懸浮控制力矩陀螺(Magnetically Suspended CMG，MSCMG)。由于MSCMG的定轉子間存在氣隙，因此具有無需潤滑、高轉速、長壽命、高精度和持續(xù)輸出大力矩的特點[3-5]。根據框架的個數，CMG可以被分為單框架CMG和雙框架CMG[6]。由于框架轉動會對轉子系統(tǒng)產生耦合力矩和干擾，而相對于雙框架而言，單框架對轉子系統(tǒng)的耦合力矩與干擾更少，有利于降低控制難度[7]。因此，單框架MSCMG更多地被應用于調整航天器姿態(tài)和抑制干擾。

具有大角動量的扁平轉子在高速旋轉時會產生較強的陀螺效應[8]，使其在平衡位置附近發(fā)生較小角度的偏轉，轉子系統(tǒng)還存在不確定干擾和不平衡振動，這些問題會降低轉子懸浮穩(wěn)定性，增加控制難度。與此同時，框架轉動所產生的耦合力矩會使轉子跳動量增加(動框架效應)，甚至碰撞保護軸承，嚴重的會造成轉子損傷[9-10]。動框架效應會使轉子大角度偏離平衡位置，即磁間隙發(fā)生較大變化，造成磁力的剛度系數發(fā)生非線性改變，降低磁力控制精度，進而降低轉子懸浮穩(wěn)定性和陀螺的輸出力矩精度[11-12]。

高速轉子在平衡位置附近發(fā)生小角度偏轉時磁間隙變化較小，因此磁力的剛度系數所發(fā)生的非線性變化對磁力的影響不大，可以對磁力模型進行線性化，因此現有控制方法可以使轉子系統(tǒng)穩(wěn)定懸浮，但不能保證轉子懸浮的位置精度。文獻[13]采用傳統(tǒng)PID(Proportional Integral Derivative)控制方法結合角速率前饋來提高轉子系統(tǒng)的穩(wěn)定性。文獻[14]基于PID控制設計了位移和速度交叉反饋器來提高系統(tǒng)的穩(wěn)定裕度。這兩種方法都只考慮了轉子的穩(wěn)定懸浮，并沒有對轉子大角度偏轉時的位置精度進行研究。文獻[15]利用含有擴展卡爾曼濾波器和狀態(tài)反饋調節(jié)器的線性二次高斯控制，提高轉子位置精度，但是該方法參數多，計算量大，不方便工程應用。文獻[16]采用變工作點線性化的方法，根據轉子位置采用與之對應的磁力模型，但該方法的控制效果取決于模型精度和不平衡大小等因素。文獻[17]提出基于電流剛度估計的自適應控制器，但沒有考慮位移剛度的非線性變化。隨著航天技術的發(fā)展，我國未來發(fā)射的航天器在數量和種類上不斷增加，傳統(tǒng)的控制方法已不能滿足新形勢下對CMG輸出高精度控制力矩的要求。

隨著控制理論的發(fā)展，智能控制方法和非線性控制方法在解決系統(tǒng)的非線性問題上有很好地表現。文獻[18]采用模糊控制器對磁軸承系統(tǒng)進行控制，提高穩(wěn)定性和魯棒性，但應用對象為磁懸浮渦輪發(fā)動機，不符合CMG輸出高精度控制力矩的要求。文獻[19]設計了神經網絡自適應估計器對磁軸承系統(tǒng)的非線性變化進行估計，提高磁力非線性的穩(wěn)態(tài)精度，但該方法只適用于控制磁軸承軸向平動，而MSCMG轉子系統(tǒng)的控制難點在磁軸承徑向方向。文獻[20]利用BP(Back Propagation)神經網絡在線調整PID控制器參數，用于五自由度磁軸承系統(tǒng)懸浮控制。文獻[21]利用前饋神經網絡逼近磁軸承參數非線性變化。文獻[22]利用神經網絡來建立磁軸承系統(tǒng)的內模模型。文獻[23]設計了自適應模糊神經網絡控制器用于磁懸浮傳輸系統(tǒng)的懸浮控制。文獻[24]利用雙積分滑模控制系統(tǒng)，調節(jié)和穩(wěn)定高度非線性的磁懸浮轉子系統(tǒng)，提高系統(tǒng)的魯棒性，但是積分運算復雜，計算量大。以上方法側重于實現磁懸浮轉子的穩(wěn)定懸浮，對提高轉子位置精度效果并不理想。由于神經網絡具有對非線性函數的逼近能力，被廣泛用來逼近非線性函數。而滑模變結構控制是一種特殊的非線性控制器，對參數變化具有魯棒性，因此應用也比較廣泛。將滑模控制結合神經網絡用于非線性系統(tǒng)的控制，完成對非線性函數的逼近與補償，可以取得很好的效果。

本文針對高速轉子受陀螺效應和動框架效應影響而偏轉時剛度系數非線性變化影響位置精度的問題，建立磁懸浮轉子非線性動力學模型并對磁力進行分析，提出神經網絡滑模控制算法，用于實現轉子的穩(wěn)定懸浮及提高位置精度。仿真結果表明本文方法在提高位置精度方面比現有方法具有更好的控制性能。

2 轉子動力學建模和磁力分析

如圖1所示，本文所研究的單框架磁懸浮控制力矩陀螺磁懸浮轉子系統(tǒng)主要由磁軸承系統(tǒng)和高速電機系統(tǒng)組成。磁懸浮轉子系統(tǒng)包括2個二自由度徑向磁軸承和2個一自由度軸向磁軸承，用于實現5個自由度的主動控制；高速電機用于驅動轉子高速旋轉。軸向位移和徑向位移由位移傳感器直接測得。基座是連接磁懸浮CMG和航天器的機械結構，CMG的輸出力矩通過基座作用到航天器上，實現調整姿態(tài)和抑制干擾。

圖1 單框架磁懸浮控制力矩陀螺結構圖Fig.1 Sectional view of the SGMSCMG

在轉子系統(tǒng)上建立空間直角坐標系，如圖2所示。磁軸承控制的5個自由度分別是質心在x，y，z3個方向上的平動和繞徑向x，y方向上的轉動運動。磁軸承力是磁懸浮轉子與定子之間的相互作用力，其中，對應Ax，Ay，Bx和By4個通道的磁力分別為fAx，fAy，fBx和fBy，可以合成為X和Y兩個方向的徑向平動力fx和fy及徑向力矩px和py；fz是軸向(z方向)上轉子所受磁軸承力的合力；lm表示從磁懸浮轉子中心到徑向磁軸承中心的距離；α，β分別為轉子繞x，y軸正方向的偏轉角度；Ω為轉子轉速。將磁軸承轉子質心的平動和轉動分別單獨考慮，建立轉子的平動運動方程和轉動運動方程，即可得到磁懸浮轉子的動力學模型。

圖2 磁懸浮CMG轉子系統(tǒng)坐標系示意圖Fig.2 Rectangular space coordinate system established on the MSCMG

徑向四通道在框架角速率為零(θg=0 (°)/s)且不考慮磁懸浮轉子重力的條件下，磁懸浮轉子的動力學模型可以描述為：

(1)

其中：m是轉子的質量；α，β分別為轉子繞x，y軸正方向的偏轉角度；Ω為轉子轉速；轉子的赤道轉動慣量為Jr，轉子的極轉動慣量為Jz。

根據磁路安培環(huán)路定律進行一系列數學推導可以得到磁力軸承承載力的計算模型：

(2)

其中：μ0為空氣磁導率，N是磁軸承線圈繞組匝數，A為定子與轉子鐵芯間氣隙的橫截面積，I是線圈電流，h是定子與轉子鐵芯間氣隙的長度，I和h為變量。由于磁力軸承采用差動勵磁方式，上下各一個電磁鐵，有兩個磁力作用于轉子，所以轉子受到的電磁力為上下磁鐵的吸力之差，即：

(3)

其中：F為總電磁力，hm0是徑向磁軸承的氣隙大小，I0是等效偏置電流，x為轉子位移(F與x的方向一致)，i為控制電流。

框架轉動會使陀螺效應下的高速轉子發(fā)生偏轉，從而導致定轉子間氣隙大小發(fā)生變化，這會使磁軸承力發(fā)生非線性改變。如果仍然采用線性模型，當氣隙變化量超過氣隙總長度的10%，控制系統(tǒng)的控制難度會增加，系統(tǒng)的穩(wěn)定性會下降。本文所用的控制力矩陀螺徑向磁軸承氣隙設計值為0.3 mm，而轉子的最大位移能夠達到60 μm，這已經遠遠超過了總長度的10%。因此，考慮磁力的非線性問題是必要的。

表1列出了磁懸浮CMG磁軸承的結構尺寸和相關參數。根據表1的數據和公式(3)，利用MATLAB對轉子在Ax通道不同位置處不同控制電流下的磁軸承力作力-位移-電流變化曲線圖，如圖3所示。可以清楚地看到，當磁懸浮轉子被偏離平衡位置時，磁力在不同電流下的非線性變化。當轉子偏離平衡位置越遠，磁力的非線性程度越高。

表1 磁懸浮CMG磁軸承結構尺寸及相關參數

圖3 磁軸承力-位移-電流變化曲線圖Fig.3 Force-displacement-current curve of MB

利用泰勒展開式分析磁力模型，由于5階以上影響較小，因此只保留到3階，可以得到：

(4)

F=kii+khx+kih2ix2+kh3x3+ki2hi2x+on.

(5)

可以看出，磁軸承力模型除了一階線性項以外，還包含高階非線性項。為方便說明，將公式(5)的非線性模型取為：

(6)

圖4 電流剛度隨氣隙大小變化曲線圖Fig.4 Current stiffness-air gap curve

表2 轉子小角度偏轉和大角度偏轉情況下剛度系數變化情況對比表

圖5 位移剛度磁間隙-控制電流關系三維曲面圖Fig.5 Displacement stiffness-air gap-current surface map

磁懸浮CMG轉子在徑向不進行主動偏轉，偏轉角度α，β為轉子被動偏轉角度，因此徑向平動方向的動力學模型為控制核心。將公式(6)代入公式(1)中的徑向平動方程，同時考慮到高速轉子的奇倍頻振動和未建模動態(tài)等干擾具有不確定性，因此加入干擾項fd，可以得到：

(7)

其中：fdx，fdy為fd在x，y方向上的分量，ix，iy為x，y方向控制電流。

以x通道為例，磁懸浮轉子的動力學方程可以表示為：

(8)

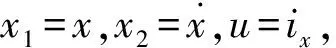
(9)

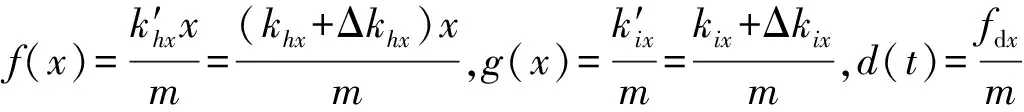
當轉子大角度偏離平衡位置時剛度系數非線性變化明顯，導致轉子位置精度下降，使CMG的輸出力矩精度降低。因此，需要設計非線性控制方法，提高轉子的位置精度從而提高CMG的輸出力矩精度。

3 神經網絡滑模控制算法設計

圖6 控制系統(tǒng)結構圖Fig.6 Structure of control system

3.1 控制器設計

定義轉子的位置誤差e為：

e=xr-x.

(10)

設計滑模面：

(11)

其中切換參數c>0。

對滑模面函數求導，并將公式(10)代入，可得：

(12)

通過RBF(Radical Basis Function)神經網絡對f和g的值進行逼近。RBF神經網絡的算法為：

(13)

f=WThf(x)+εf，
g=VThg(x)+εg，

(14)

(15)

(16)

由公式(12)可以導出控制律：

(17)

其中趨近速率η≥D。

3.2 穩(wěn)定性分析

保持控制系統(tǒng)穩(wěn)定是實現轉子位置高精度控制的基礎，而神經網絡滑模控制算法的穩(wěn)定性與控制律中非線性函數的權值調整過程密切相關。利用Lyapunov函數對系統(tǒng)進行穩(wěn)定性分析，進而可以得到基于自適應算法的網絡權值更新規(guī)則。

將公式(12)代入公式(11)，可以得到：

(18)

其中：

定義閉環(huán)系統(tǒng)的Lyapunov函數為：

(19)

其中：自適應學習率γ1>0，γ2>0。

對L求導并將公式(18)代入，可得：

(20)

設計自適應算法：

(21)

將公式(21)代入公式(20)，可得：

(22)

圖7是磁軸承徑向單通道RBF神經網絡滑模控制框圖。其中Ka是功放增益，Ks是傳感器增益，d為擾動。

圖7 單通道RBF神經網絡滑模控制框圖Fig.7 Control block diagram of single channel

4 仿真和實驗結果

為了驗證磁懸浮轉子系統(tǒng)在剛度系數非線性變化和干擾力的影響下，神經網絡滑模控制對轉子位置精確控制的有效性，本文基于Matlab/Simulink軟件分別搭建了神經網絡滑模控制系統(tǒng)和傳統(tǒng)PID控制系統(tǒng)，用于比較兩種方法的控制效果。首先對轉子沿徑向X軸方向平動控制進行研究，分別對比兩種方法輸入信號為正弦和階躍時的位置精度。其次，在框架轉動時高速轉子受徑向Y通道耦合作用和干擾影響而偏離平衡位置的情況下，對比兩種方法對轉子期望位置的控制精度，驗證本文方法對轉子高精度位置控制的有效性。利用實驗平臺，分別采用傳統(tǒng)PID控制和神經網絡滑模控制，進行徑向單通道的平動控制實驗和動框架效應下偏轉轉子位置控制實驗。

表3 傳統(tǒng)PID方法初始參數及優(yōu)化結果

表4 神經網絡滑模控制參數

4.1 徑向X通道平動控制仿真

本文研究的磁懸浮CMG框架伺服系統(tǒng)最大設計轉速為±15 (°)/s2，即最大角速率為1.632 8 rad/s，設置正弦輸入為0.1sin 1.632 8tmm。其仿真結果如圖8所示(彩圖見期刊電子版)。圖8(a)為兩種控制方法對輸入信號的控制效果，其中紅色實線為理想位置，藍色虛線為神經網絡滑模控制方法，藍色點線為傳統(tǒng)PID控制方法；可以看出本文方法穩(wěn)態(tài)誤差更小，僅為0.000 1 mm。圖8(b)為兩種方法的誤差對比圖，紅色實線為本文方法的誤差，藍色點線為傳統(tǒng)PID方法的誤差；從中可以看出本文方法的位置誤差不到傳統(tǒng)PID方法的5%。

(a)兩種方法的位置對比 (a)Position comparison

(b)位置誤差對比 (b)Comparison of position error圖8 轉子平動方向正弦輸入控制效果Fig.8 Control effect of sinusoidal input in translational direction

將轉子平動方向階躍輸入設置為0.1arctan 20t，其控制位置的仿真結果如圖9所示(彩圖見期刊電子版)。圖9(a)表示兩種方法對輸入信號的控制效果，其中紅色實線為理想位置，藍色虛線為神經網絡滑模控制方法，藍色點線為傳統(tǒng)PID控制方法；本文方法的穩(wěn)態(tài)誤差僅為0.000 1 mm。圖9(b)為兩種方法的誤差對比圖，從中可以看出傳統(tǒng)PID方法控制過程轉子位置存在較大幅度的波動，而本文方法波動極小。

(a)兩種方法位置控制效果 (a)Position comparison

(b)位置誤差對比 (b)Comparison of position error圖9 轉子平動方向階躍輸入控制效果Fig.9 Control effect of step input in translational direction

4.2 偏轉轉子位置控制仿真

為驗證本方法在轉子受到由框架轉動及其他不確定干擾時，仍能精確控制轉子，保證其穩(wěn)定懸浮并輸出高精度力矩，通過對比轉子偏離平衡位置的位移來比較本文方法與傳統(tǒng)方法的控制效果。

根據CMG的設計參數和實際運行情況，在仿真中加入偏轉力模擬動框架效應，加入干擾力模擬實際運行過程中存在的奇數倍頻和不確定擾動。干擾設定為：

d(t)=0.2sin 1.632 8t+0.1sin 1 570t+
0.05sin 4 710t+random(σ2=0.1)(N).

如圖10所示。其中0.2sin 1.632 8t是使轉子在徑向產生偏轉的干擾力，0.1sin 1 570t和0.05sin 4 710t分別是轉子在額定轉速15 000 r/min下的同頻和三倍頻不平衡振動干擾，random(σ2=0.1)是模擬實際運行過程中的隨機干擾。

圖10 轉子所受干擾力Fig.10 Disturbance force

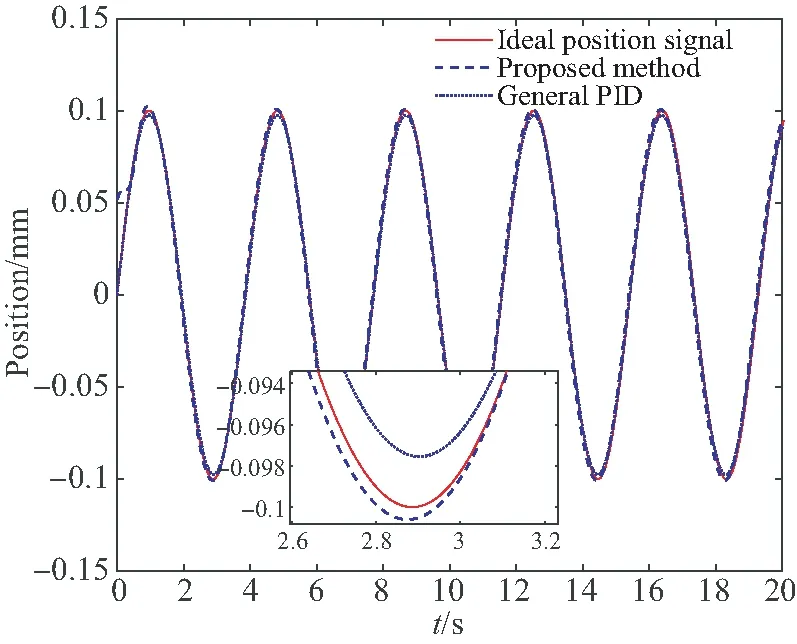
當輸入為正弦信號時，采用本文方法和傳統(tǒng)PID控制方法的位置控制效果如圖11(a)所示(彩圖見期刊電子版)，其中紅色實線表示理想位置，藍色虛線表示本文方法的控制位置，藍色點線為傳統(tǒng)PID的位置。圖11(b)為兩種方法誤差對比，可以看出本文方法的位置誤差僅為0.000 2 mm，是傳統(tǒng)PID方法的0.5%，這說明本文方法在轉子大角度偏轉時仍能夠保證位置的高精度控制。圖11(c)中，紅色實線和藍色虛線分別表示X和Y兩通道的控制電流隨時間變化情況，可以看出本文方法控制電流波動明顯小于傳統(tǒng)方法。

(a)兩種方法的位置對比 (a)Position comparison

(b)位置誤差對比 (b)Comparison of position error

(c)本文方法和傳統(tǒng)方法雙通道控制電流 (c)Control current of proposed method and general PID method圖11 雙通道偏轉轉子正弦輸入控制效果Fig.11 Control effect of sinusoidal input for tilted rotor

當輸入為階躍信號時，采用本文方法和傳統(tǒng)PID控制方法的位置控制效果如圖12(a)所示(彩圖見期刊電子版)，其中紅色實線表示理想位置，藍色虛線表示本文方法的控制位置，藍色點線為傳統(tǒng)PID的位置。從圖12(b)中可以看出，本文方法的位置誤差僅為傳統(tǒng)PID的0.125%，這說明當轉子突然收到干擾時，本文方法仍能對轉子進行高精度地位置控制。圖12(c)中，紅色和藍色實線分別表示X和Y兩通道的控制電流隨時間變化情況，可以看出本文方法為保證轉子位置精度，控制電流在輸入信號階躍的時刻調整頻率更高。

(a)兩種方法的位置對比 (a)Position comparison

(b)位置誤差對比 (b)Comparison of position error

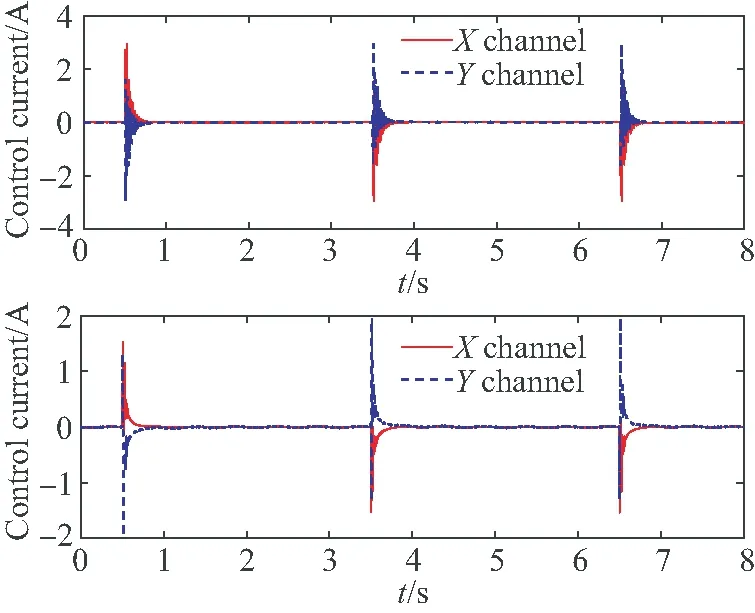
(c)本文方法和傳統(tǒng)PID方法雙通道控制電流 (c)Control current of the proposed method and general PID method圖12 雙通道偏轉轉子階躍輸入控制效果Fig.12 Control effect of step input for tilted rotor

4.2 實驗驗證

為了驗證所提出的控制方法對提高轉子位置精度的有效性，類似于仿真驗證的條件，分別采用傳統(tǒng)PID控制和神經網絡滑模控制，進行徑向單通道的平動控制實驗。令框架轉速為0 (°)/s，將轉子升速至15 000 r/min。實驗結果如圖13所示。

(a)傳統(tǒng)PID控制 (a)General PID method

(b)所提出方法 (b)Proposed method圖13 徑向單通道平動控制轉子位移曲線Fig.13 Position curve of the rotor in translational direction

從圖13中可以看出，傳統(tǒng)PID控制方法下，轉子平動位移最大可達1 μm，而本文所提出方法轉子最大位移僅為0.3 μm，位置精度比傳統(tǒng)方法提高了70%。

為了驗證框架轉動情況下，轉子受動框架效應而發(fā)生偏轉時的位置精度，給框架系統(tǒng)的頻率為3 Hz，幅值為10 (°)/s的正弦參考信號，兩種控制方法下的轉子位置精度如圖14所示。從圖中可以看出，動框架效應下，傳統(tǒng)PID控制方法轉子最大位移為10 μm，而本文所提方法轉子最大位移為4 μm，轉子位置精度提高了60%。

(a)傳統(tǒng)PID控制 (a)General PID method

(b) 所提出方法 (b)Proposed method圖14 動框架時偏轉轉子位移曲線Fig.14 Position of the tilted rotor under moving-gimbal effect

上述實驗結果與仿真結果相符甚佳。然而，與仿真結果相比，在轉子位移曲線中存在更加明顯地高頻振蕩，并且實驗中的位置誤差更大。原因是在實際系統(tǒng)中還存在更多的不確定干擾和傳感器噪聲等因素。仿真和實驗結果均驗證了神經網絡滑模控制方法可以有效提高MSCMG的轉子位置精度。

5 結 論

磁懸浮控制力矩陀螺通過改變角動量方向輸出控制力矩，具有高精度、輸出力矩大等特點，能夠對航天器進行高精度姿態(tài)控制。實現磁懸浮轉子的高精度位置控制可以大大提高轉子系統(tǒng)的穩(wěn)定性和懸浮精度，這是磁懸浮CMG能夠輸出高精度控制力矩的前提之一。高速轉子存在陀螺效應和不平衡振動，在干擾下更容易出現位移偏差，增加控制難度。當框架轉動時，轉子會較大程度偏離平衡位置，導致磁軸承間隙發(fā)生變化，這會引起位移剛度和電流剛度的非線性變化，從而使磁力發(fā)生非線性改變，降低轉子位置精度，影響轉子穩(wěn)定懸浮，進一步影響磁懸浮CMG的輸出力矩精度。

為解決上述問題，本課題針對非線性磁力模型，分析了位移剛度和電流剛度的非線性變化對磁力的影響；建立了磁懸浮轉子二階非線性不確定系統(tǒng)模型；設計了適用于轉子徑向平動控制和偏轉情況下位置控制的神經網絡滑模控制算法，并進行了仿真研究。在轉子單通道平動控制中，與傳統(tǒng)PID方法仿真結果對比，本文方法的穩(wěn)態(tài)誤差為0.000 1 mm，不到傳統(tǒng)PID方法的5%，表明該方法有效提高了轉子穩(wěn)定懸浮的位置精度和抑制干擾能力；在考慮徑向各通道耦合的偏轉轉子位置控制仿真中，與傳統(tǒng)交叉反饋方法結果對比，本文方法穩(wěn)態(tài)誤差0.000 2 mm，僅為交叉反饋方法的0.125%，表明該方法能夠更加有效地抑制陀螺效應，并提高轉子的位置精度。實驗結果表明，與傳統(tǒng)PID方法相比，所提出方法的轉子位置精度提高了60%以上。綜合以上結果，證明了神經網絡滑模控制能夠更好地解決磁軸承系統(tǒng)的非線性問題。