改進多尺度幅值感知排列熵與隨機森林結合的滾動軸承故障診斷

吳海濱，陳寅生*，張庭豪，汪 穎

(1.哈爾濱理工大學 測控技術與通信工程學院，黑龍江 哈爾濱 150080；2.哈爾濱工業大學 電氣工程及自動化學院，黑龍江 哈爾濱 150080)

1 引 言

滾動軸承是旋轉機械中最常見的連接部件之一，但由于磨損、疲勞、腐蝕、過載等諸多因素的影響，滾動軸承在工作過程中極易發生故障[1-6]，進而影響機械設備的整體性能。因此，滾動軸承的故障診斷及嚴重程度分析對保證機械設備運行的可靠性及制定相應維修策略具有重要意義。

滾動軸承故障的位置及嚴重程度導致其振動信號的沖擊特性存在明顯差異。因此，基于振動信號的故障診斷技術成為當前滾動軸承異常狀態監測的重要研究方向之一[7]。滾動軸承故障診斷的本質是一個模式識別過程，主要包括特征提取和故障分類[8-9]。但是，滾動軸承振動信號具有非線性和非平穩的特點，同時運行過程中容易受到多種外界因素的干擾，信噪比較低，導致軸承故障特征難以得到有效提取，影響故障診斷的識別準確率。

鑒于此，相關學者針對滾動軸承故障診斷展開了大量的研究工作。文獻[7]利用集合經驗模態分解(Ensemble Emprical Mode Decompositon，EEMD)實現對滾動軸承振動信號的自適應分解，并采用峭度值結合相關系數的方法確定包含主要軸承狀態信息的本征模態函數，再利用其奇異值作為特征向量，通過超球多類支持向量機實現對滾動軸承的多故障分類。然而，EEMD不能夠完全解決EMD的模態混疊問題，峭度值結合相關系數的本征模態函數選擇法會損失部分軸承故障信息，而超球多類支持向量機的核參數選取和優化過于復雜，增加了實際應用的困難。文獻[10]利用局部均值分解(LMD)算法對滾動軸承振動信號進行預處理，再利用多尺度熵(MSE)提取故障特征向量，最后構建BP神經網絡分類器實現故障類型識別。但是，在時間序列的粗粒化過程中，MSE的序列長度會隨著尺度因子的增加而縮短。當尺度因子較大時，多尺度熵值具有不穩定性，進而影響特征提取的有效性。文獻[11]利用多尺度排列熵提取滾動軸承振動信號中的故障特征，并采用Laplacian Score算法進行特征選擇，隨后通過支持向量機(SVM)實現故障類型識別。然而，基于排列熵的特征提取忽略了時間序列中元素幅值對熵值的影響，使得提取的故障特征具有較大的隨機性，進而影響故障識別的準確率。

由于現有基于滾動軸承振動信號的故障診斷方法尚存在特征提取可分性不強、故障識別準確率較低及故障嚴重程度分析不充分等問題，本文提出了一種基于改進多尺度幅值感知排列熵(Improved Multiscale Amplitude-Aware Permutation Entropy， IMAAPE)與隨機森林(Random Forest， RF)分類器的滾動軸承故障診斷方法。首先，采用固有時間尺度分解(Intrinsic Timescale Decomposition， ITD)對滾動軸承振動信號進行分解，選取最佳固有旋轉分量，改善EMD分解結果的欠包絡和過包絡問題，并有效抑制了模態混疊和端點效應。然后，利用IMAAPE提取最佳固有旋轉分量中蘊含的滾動軸承故障特征，改善了多尺度分析中的粗粒化過程，提升了故障特征提取的穩定性，同時在計算排列熵過程中引入相對規范化概率，增加對故障信號幅值和頻率變化的敏感特性，有效提取故障類型與嚴重程度特征。最后，利用隨機森林分類器泛化能力強、參數設置簡便、訓練速度快等優點，實現對滾動軸承不同故障類型的識別及嚴重程度分析。

2 固有時間尺度分解

(1)

ITD算法的主要步驟如下：

Step1：假設{τk，k=1，2，…}表示信號Xt的局部極值，默認τ0=0。

Step2：在區間[0，τk]中定義了Lt和Ht，且Xt在t∈[0，τk+2]的區間內有效。那么，在連續極值間隔(τk，τk+1]中提取的基線信號Lt表示為：

(2)

其中：

(3)

其中：α是線性縮放因子，用來調節提取固有旋轉分量幅度，α∈[0，1]，通常取α=0.5。

Step3：根據式(2)和式(3)，固有旋轉分量Ht可以表示為：

(4)

Step4：將基線信號Lt作為下一次分解的輸入信號，重復步驟1～3，獲取一系列PR分量。分解的終止條件為基線信號Lt變得單調或者小于某個預設值。

經過ITD分解后，時間序列Xt被分解為一系列PR分量和一個單調趨勢分量。信號峰度能有效描述信號的脈沖特性。峰度值越高，信號所包含的脈沖特征越豐富。因此，定義峰度值最大的PR分量為最佳固有旋轉分量，其計算過程如下[13-14]：

(5)

(6)

其中：Ki表示第i個PR分量的峰度值，n表示時間序列長度。Ui為第i個PR分量的歸一化峰度值，m是PR分量的個數。最佳固有旋轉分量選取Ui為最大值時所對應的PR分量。

3 基于IMAAPE的特征提取

3.1 改進多尺度熵

僅從單一尺度對時間序列進行熵值分析，可能會損失原始信號的部分重要信息。因此，Costa等于2007年提出了多尺度熵(Multi-scale Entropy， MSE)[15]，實現對復雜信號在不同時間尺度下的特征信息提取，其定義如下：

假設一個長度為N的時間序列{Xi}={x1，x2，…，xN}，利用尺度因子τ=1，2，…，n，對序列進行粗粒化，粗粒化過程如下：

(7)

圖1 尺度因子τ=2和τ=3下改進多尺度熵的粗粒化過程

Fig.1 Improved coarse-graining procedures for scalefactorτ=2 andτ=3

隨后，計算每個粗粒化的新時間序列的樣本熵值，獲得不同時間尺度下的n個多尺度熵值來描述原始時間序列的信號特征。然而，在粗粒化過程中，MSE的時間序列的長度將縮短為N/τ。尺度因子τ越大，經粗粒化后的時間序列長度越短，這將影響后續對熵值的度量，降低特征提取效果。為了解決該問題，相關學者對MSE的粗粒化過程進行改進[16]，解決了MSE粗粒化后時間序列長度縮短的問題，改進多尺度熵的粗粒化過程如圖1所示。改進后的粗粒化時間序列表示為：

(8)

3.2 幅值感知排列熵

Bandt等于2002年提出排列熵(Permutation Entropy， PE)的概念[17]，目前PE廣泛應用于對復雜時間序列信號的分析，以衡量一個非線性、非平穩性信號的復雜度。

每個排列順序πi出現的概率表示為：

(9)

(10)

然而，通過排列熵描述復雜時間序列還存在兩個主要問題。第一，傳統PE僅考慮了時間序列幅值的排列次序，而忽略了對應的時間序列中元素的幅值信息；第二，時間序列中幅值相等的元素對PE值的影響并沒有清晰說明。鑒于此，文獻[18]提出了幅值感知排列熵(Amplitude-Aware Permutation Entropy， AAPE)，以提升PE對時間序列的幅值和頻率的敏感特性。不同于排列熵算法，AAPE算法考慮了信號振幅的均值及振幅之間的偏差，引入了相對規范化概率替代PE中f(πi)的計數規則。

(11)

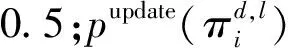
(12)

時間序列的AAPE可表示為：

(13)

3.3 改進多尺度幅值感知排列熵

IMAAPE算法借鑒了改進多尺度熵算法中的粗粒化過程，突出不同時間尺度下的信號特征，再利用AAPE對信號幅值和頻率變化敏感的特性，提取不同時間尺度下的信號特征。該方法的主要計算步驟如下：

(14)

4 隨機森林分類器

RF由美國科學院院士Breiman L.于2001年提出，該算法適用于解決預測與分類問題[19-20]。RF集成了多個弱分類器，由眾多決策樹組成，其輸出結果根據森林中每棵決策樹的預測結果，利用投票原則確定。RF的實現過程簡單，具有較高的識別準確率，在故障診斷領域具有廣泛應用[21-22]。RF的基本原理如下：

假設隨機森林分類器由多個決策樹{hj(x，Θk)，k=1，2，…，n}組成，{Θk，k=1，2，…，n}表示相互獨立且同分布的隨機向量。隨機森林分類器的訓練樣本集表示為D={(x1，y1)，(x2，y2)，…，(xN，yN)}，xi=(xi，1，…，xi，p)T表示第i個訓練樣本，xi具有p個特征值，yi表示訓練樣本xi對應的標簽。對訓練樣本集D進行n次Bootstrap采樣，獲得n個Bootstrap子樣本Dj(j=1，2，…，n)。針對每個子樣本Dj，構建決策樹模型hj(x)(一般選用CART決策樹)，最終獲得由一組決策樹{h1(x)，h2(x)，…，hk(x)}組成的決策樹分類器。對于一個新的測試樣本，通過n個決策樹投票，得到最多票數的類別作為測試樣本的最終類別，分類決策如下：

(15)

其中：hj(x)代表第j棵決策樹；I(·)為示性函數，即當集合內有此數時值為1，否則值為0；y表示類別標簽yi構成的目標變量。

5 滾動軸承故障診斷方法流程

本文提出的故障診斷方法能夠實現滾動軸承內環、外環及滾珠故障識別及故障嚴重程度分析，該方法的故障識別及故障嚴重程度分析流程如圖2所示。

本文提出的滾動軸承故障診斷方法改進了多尺度熵的粗粒化過程，并利用幅值感知排列熵提取振動信號特征，提升滾動軸承故障特征的可分性，再通過隨機森林分類器進行故障類型識別及故障嚴重程度分析。

圖2 故障識別及故障嚴重程度分析流程Fig.2 Flow chart of fault identification and severity analysis

該方法通過IMAAPE對不同故障類型及故障嚴重程度(故障直徑)的數據樣本進行特征提取，描述故障嚴重程度特征，再利用RF良好的分類性能對故障類型及嚴重程度進行判斷，具體流程描述如下：

Step1：獲取不同故障程度下的滾動軸承振動信號，并組成不同故障程度下的滾動軸承振動信號樣本集；

Step2：針對樣本集中的每一個振動信號，進行ITD，獲取一系列PR分量，并從中選取最優PR分量進行后續特征提取；

Step3：利用IMAAPE提取最優PR分量不同時間尺度下包含的滾動軸承振動信號的幅值和頻率特征，組成不同故障程度下的故障特征向量；

Step4：通過對滾動軸承振動信號樣本集進行特征提取，可以組成滾動軸承振動信號故障特征集，并利用該特征集構建RF多分類器；

Step5：對待測試的滾動軸承振動信號進行ITD分解，選取最優PR分量提取故障特征向量，將該特征向量輸入到RF分類器中，得到滾動軸承故障類型和故障嚴重程度。

6 實驗與分析

6.1 實驗數據

本文選用美國凱斯西儲大學軸承數據中心[23]提供的滾動軸承故障數據集對所提出的故障診斷方法進行實驗驗證，滾動軸承實驗平臺如圖3所示。實驗以SKF軸承作為研究對象，數據集通過加速度傳感器采集正常(NM)、內環故障(IR)、外環故障(OR)及滾珠故障(B)4種狀態下的軸承振動信號。加速度計安裝在電機外殼的驅動端和風扇端的12點鐘方向，采樣頻率為12 kHz。對于三種故障類型，分別選取故障直徑為2.13，4.27和6.4 mm三種不同的故障嚴重程度進行樣本采集。2 237.1 W負載下不同故障嚴重程度的滾動軸承振動信號的時域波形如圖4所示，可見其振動信號的幅值和頻率的變化與故障類型和故障嚴重程度的變化緊密相關。表1所示為本文中實驗樣本的軸承負載、故障類型及嚴重程度組成。實驗樣本一共包括3種不同的滾動軸承故障類型，每種故障類型分為3種不同的故障嚴重程度。將每種軸承數據不重疊地分割成多個數據樣本，每個樣本中含有N=1 024個采樣點，組成每種故障嚴重程度下50個樣本構成的實驗數據集。實驗中，采用每種故障嚴重程度下10個樣本作為訓練集，40個樣本作為測試集。

圖3 凱斯西儲大學滾動軸承實驗平臺Fig.3 Rolling bearing experimental platform of Case Western Reserve University

圖4 負載2 237.1 W下不同故障嚴重程度的滾動軸承振動信號Fig.4 Vibration signals of rolling bearing with different fault severity under 2 237.1 W

表1 實驗樣本的故障類型及嚴重程度組成

6.2 滾動軸承故障特征提取實驗

在執行滾動軸承故障特征提取前，需采用ITD對振動信號進行預處理，進一步突顯信號固有瞬時幅值、頻率等形態特征。圖5所示為故障直徑為2.13 mm下滾珠故障的振動信號ITD分解實驗結果。ITD將故障振動信號分解為5個PR分量和1個單調趨勢分量。由分解結果可見，最優PR分量包含描述滾珠故障振動信號中的主要幅值和頻率特征。

滾動軸承振動信號經ITD分解后，采用IMAAPE進行特征提取。對最優PR分量進行IMAAPE特征提取，設置嵌入維數d=4，時間延遲l=1，時間尺度τ=20，調整系數A=0.5。對測試集的振動信號樣本進行IMAAPE特征提取，得到20維的滾動軸承振動信號故障特征向量。圖6所示為0負載下不同故障直徑的IMAAPE特征聚類圖，從特征向量的前3個維度可以看出，本文提出的特征提取方法能夠較好地對正常、內環故障、外環故障及滾珠故障進行描述，特征向量具有較強的聚類性。圖7所示為0負載下不同故障嚴重程度的IMAAPE特征聚類圖，選取特征向量中前2個維度可以看出，本文提出的特征提取方法對不同故障嚴重程度的特征提取結果也具有較好的聚類性。

圖5 故障直徑2.13 mm下滾珠故障的ITD分解結果Fig.5 ITD decomposition results of ball fault under fault diameter of 2.13 mm

為了說明IMAAPE滾動軸承振動信號特征提取方法的性能，本文將IMAAPE與現有滾動軸承故障特征提取方法的效果進行對比。實驗采用0負載下內環故障、外環故障和滾珠故障各40個樣本進行分析，實驗結果如表2所示。不同故障類型情況下，特征向量的類間距離平均值越大，表示特征提取方法提取的不同故障類型的特征差異性越大；不同故障類型情況下特征向量的類內距離平均值越小，表示特征提取方法提取的相同故障類型的特征差異性越小。由表2可見，IMAAPE的平均類間距離大于改進多尺度排列熵[11](IMPE)和精細復合多尺度排列熵[25](RCMPE)，但小于改進多尺度樣本熵[26](IMSE)、改進多尺度模糊熵[11](IMFE)和精細復合多尺度樣本熵[25](RCMSE)，而IMAAPE的平均類內距離在所有特征提取方法中最小。該實驗結果說明IMAAPE提取的滾動軸承故障特征具有較好的聚類性質。此外，由表2可知，在計算相同的采樣點數的樣本時，IMAAPE的平均耗時為所有特征提取方法中最小的，具有較好的實時性。表3為故障程度識別準確率的比較。

(a)故障直徑2.13 mm(a)Fault diameter of 2.13 mm(b)故障直徑4.27 mm(b)Fault diameter of 4.27 mm(c)故障直徑6.4 mm(c)Fault diameter of 6.4 mm圖6 負載0下不同故障直徑的IMAAPE特征聚類圖Fig.6 IMAAPE feature clustering diagram of different fault diameters under zero load

表2 滾動軸承故障特征提取算法的性能比較

圖7 0負載下不同故障嚴重程度的IMAAPE特征聚類圖Fig.7 Clustering diagram of IMAAPE features with different fault severity under zero load

為了進一步說明本文提出的IMAAPE故障特征提取方法的可分性，本文分別利用表2中描述的特征提取方法與RF分類器相結合，設置CART決策樹數量為50，對滾動軸承10種不同健康狀態下的每種類別40個測試樣本進行分析，實驗結果如表4所示。由實驗結果可知，與當前不同滾動軸承故障特征提取方法相比較，本文提出的IMAAPE故障特征提取方法具有更好的故障嚴重程度描述能力，提取的特征向量具有更高的可分性。

表3 滾動軸承故障特征提取算法準確率比較

6.3 滾動軸承故障類型識別實驗

為了驗證IMAAPE與RF相結合的軸承故障診斷方法的性能，對滾動軸承10種不同健康狀態下的每種類別40個測試樣本進行實驗驗證，結果如表5所示。可見，提出的滾動軸承故障診斷方法能夠有效地識別正常、內環故障、外環故障、滾珠故障，并且能夠較為有效地分析故障嚴重程度，誤報率較低，平均識別準確率高達99.25%。

表4 不同滾動軸承故障診斷方法識別率比較

表5 滾動軸承故障診斷方法的識別率

為了進一步說明本文提出方法在滾動軸承故障診斷中的性能，將本文提出的滾動軸承故障診斷方法與現有方法進行比較，實驗結果如表5所示。可見，本文提出的方法能夠實現滾動軸承故障類型識別，并能夠進一步分析軸承故障的嚴重程度。在不考慮故障嚴重程度的情況下，能夠準確識別故障類型，故障識別準確率達到100%；在考慮故障嚴重程度的情況下，提出的故障診斷方法具有故障嚴重程度分析能力，且具有相對較高的平均故障識別率，達到99.25%。

7 結 論

ITD能夠穩定地將滾動軸承故障信號分解為一組PR分量，其中最優PR分量能夠突顯滾動軸承故障信號的沖擊特征，適用于滾動軸承振動信號的時-頻分析。IMAAPE改善了多尺度分析中的粗粒化過程，并利用幅值感知排列熵對信號幅值和頻率變化敏感的特性，計算不同時間尺度下的AAPE值并組成特征向量，具有較強的故障描述能力且實時性較好。基于IMAAPE與RF的滾動軸承故障診斷方法能夠在準確識別故障類型的基礎上，進一步對故障嚴重程度進行分析，在考慮故障嚴重程度的情況下，平均故障識別準確率達到99.25%。

本文方法目前僅適用于滾動軸承固定負載下的故障類型識別及故障嚴重程度分析。為了進一步提升該滾動軸承故障診斷方法的泛化能力，后續的研究重點為變負載情況下滾動軸承的故障類型與故障嚴重程度分析。